Spaces:
Runtime error
Runtime error
| title: ECE | |
| datasets: | |
| - | |
| tags: | |
| - evaluate | |
| - metric | |
| description: binned estimator of expected calibration error | |
| sdk: gradio | |
| sdk_version: 3.0.2 | |
| app_file: app.py | |
| pinned: false | |
| # Metric Card for ECE | |
| ## Metric Description | |
| <!--- | |
| *Give a brief overview of this metric, including what task(s) it is usually used for, if any.* | |
| --> | |
| Expected Calibration Error *ECE* is a popular metric to evaluate top-1 prediction miscalibration. | |
| It measures the L^p norm difference between a model’s posterior and the true likelihood of being correct. | |
| 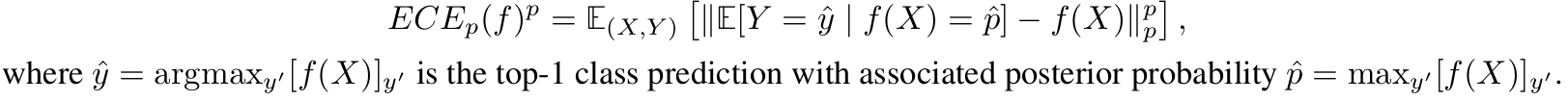 | |
| It is generally implemented as a binned estimator that discretizes predicted probabilities into ranges of possible values (bins) for which conditional expectation can be estimated. | |
| ## How to Use | |
| <!--- | |
| *Give general statement of how to use the metric* | |
| *Provide simplest possible example for using the metric* | |
| --> | |
| ``` | |
| >>> metric = evaluate.load("jordyvl/ece") | |
| >>> results = metric.compute(references=[0, 1, 2], predictions=[[0.6, 0.2, 0.2], [0, 0.95, 0.05], [0.7, 0.1 ,0.2]]) | |
| >>> print(results) | |
| {'ECE': 0.1333333333333334} | |
| ``` | |
| For valid model comparisons, ensure to use the same keyword arguments. | |
| ### Inputs | |
| <!--- | |
| *List all input arguments in the format below* | |
| - **input_field** *(type): Definition of input, with explanation if necessary. State any default value(s).* | |
| --> | |
| ### Output Values | |
| <!--- | |
| *Explain what this metric outputs and provide an example of what the metric output looks like. Modules should return a dictionary with one or multiple key-value pairs, e.g. {"bleu" : 6.02}* | |
| *State the range of possible values that the metric's output can take, as well as what in that range is considered good. For example: "This metric can take on any value between 0 and 100, inclusive. Higher scores are better."* | |
| #### Values from Popular Papers | |
| *Give examples, preferrably with links to leaderboards or publications, to papers that have reported this metric, along with the values they have reported.* | |
| --> | |
| As a metric of calibration *error*, it holds that the lower, the better calibrated a model is. Depending on the L^p norm, ECE will either take value between 0 and 1 (p=2) or between 0 and \infty_+. | |
| The module returns dictionary with a key value pair, e.g., {"ECE": 0.64}. | |
| ### Examples | |
| <!--- | |
| *Give code examples of the metric being used. Try to include examples that clear up any potential ambiguity left from the metric description above. If possible, provide a range of examples that show both typical and atypical results, as well as examples where a variety of input parameters are passed.* | |
| --> | |
| ```python | |
| N = 10 # N evaluation instances {(x_i,y_i)}_{i=1}^N | |
| K = 5 # K class problem | |
| def random_mc_instance(concentration=1, onehot=False): | |
| reference = np.argmax( | |
| np.random.dirichlet(([concentration for _ in range(K)])), -1 | |
| ) # class targets | |
| prediction = np.random.dirichlet(([concentration for _ in range(K)])) # probabilities | |
| if onehot: | |
| reference = np.eye(K)[np.argmax(reference, -1)] | |
| return reference, prediction | |
| references, predictions = list(zip(*[random_mc_instance() for i in range(N)])) | |
| references = np.array(references, dtype=np.int64) | |
| predictions = np.array(predictions, dtype=np.float32) | |
| res = ECE()._compute(predictions, references) # {'ECE': float} | |
| ``` | |
| ## Limitations and Bias | |
| <!--- | |
| *Note any known limitations or biases that the metric has, with links and references if possible.* | |
| --> | |
| See [3],[4] and [5]. | |
| ## Citation | |
| [1] Naeini, M.P., Cooper, G. and Hauskrecht, M., 2015, February. Obtaining well calibrated probabilities using bayesian binning. In Twenty-Ninth AAAI Conference on Artificial Intelligence. | |
| [2] Guo, C., Pleiss, G., Sun, Y. and Weinberger, K.Q., 2017, July. On calibration of modern neural networks. In International Conference on Machine Learning (pp. 1321-1330). PMLR. | |
| [3] Nixon, J., Dusenberry, M.W., Zhang, L., Jerfel, G. and Tran, D., 2019, June. Measuring Calibration in Deep Learning. In CVPR Workshops (Vol. 2, No. 7). | |
| [4] Kumar, A., Liang, P.S. and Ma, T., 2019. Verified uncertainty calibration. Advances in Neural Information Processing Systems, 32. | |
| [5] Vaicenavicius, J., Widmann, D., Andersson, C., Lindsten, F., Roll, J. and Schön, T., 2019, April. Evaluating model calibration in classification. In The 22nd International Conference on Artificial Intelligence and Statistics (pp. 3459-3467). PMLR. | |
| [6] Allen-Zhu, Z., Li, Y. and Liang, Y., 2019. Learning and generalization in overparameterized neural networks, going beyond two layers. Advances in neural information processing systems, 32. | |
| ## Further References | |
| <!--- | |
| *Add any useful further references.* | |
| --> |