Spaces:
Runtime error
Runtime error
File size: 4,720 Bytes
2ff3652 b81628e ac1bb79 2ff3652 b81628e 2ff3652 b81628e ac1bb79 b81628e ac1bb79 0736615 0c94397 2afab11 0736615 ac1bb79 b81628e ac1bb79 b81628e 0736615 b81628e 0736615 0c94397 b81628e ac1bb79 b81628e ac1bb79 b81628e ac1bb79 b81628e ac1bb79 0736615 ac1bb79 b81628e ac1bb79 b81628e ac1bb79 9d4511f 0736615 b81628e 0c94397 b81628e ac1bb79 b81628e ac1bb79 0c94397 b81628e ac1bb79 0736615 ac1bb79 0736615 ac1bb79 0736615 ac1bb79 0736615 ac1bb79 0736615 0c94397 b81628e 0736615 b81628e 0736615 |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 |
---
title: ECE
datasets:
-
tags:
- evaluate
- metric
description: binned estimator of expected calibration error
sdk: gradio
sdk_version: 3.0.2
app_file: app.py
pinned: false
---
# Metric Card for ECE
## Metric Description
<!---
*Give a brief overview of this metric, including what task(s) it is usually used for, if any.*
-->
Expected Calibration Error *ECE* is a popular metric to evaluate top-1 prediction miscalibration.
It measures the L^p norm difference between a model’s posterior and the true likelihood of being correct.
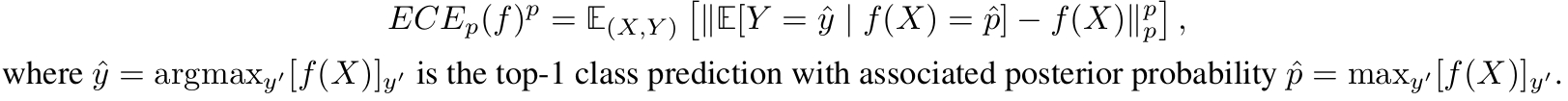
It is generally implemented as a binned estimator that discretizes predicted probabilities into ranges of possible values (bins) for which conditional expectation can be estimated.
## How to Use
<!---
*Give general statement of how to use the metric*
*Provide simplest possible example for using the metric*
-->
```
>>> metric = evaluate.load("jordyvl/ece")
>>> results = metric.compute(references=[0, 1, 2], predictions=[[0.6, 0.2, 0.2], [0, 0.95, 0.05], [0.7, 0.1 ,0.2]])
>>> print(results)
{'ECE': 0.1333333333333334}
```
For valid model comparisons, ensure to use the same keyword arguments.
### Inputs
<!---
*List all input arguments in the format below*
- **input_field** *(type): Definition of input, with explanation if necessary. State any default value(s).*
-->
### Output Values
<!---
*Explain what this metric outputs and provide an example of what the metric output looks like. Modules should return a dictionary with one or multiple key-value pairs, e.g. {"bleu" : 6.02}*
*State the range of possible values that the metric's output can take, as well as what in that range is considered good. For example: "This metric can take on any value between 0 and 100, inclusive. Higher scores are better."*
#### Values from Popular Papers
*Give examples, preferrably with links to leaderboards or publications, to papers that have reported this metric, along with the values they have reported.*
-->
As a metric of calibration *error*, it holds that the lower, the better calibrated a model is. Depending on the L^p norm, ECE will either take value between 0 and 1 (p=2) or between 0 and \infty_+.
The module returns dictionary with a key value pair, e.g., {"ECE": 0.64}.
### Examples
<!---
*Give code examples of the metric being used. Try to include examples that clear up any potential ambiguity left from the metric description above. If possible, provide a range of examples that show both typical and atypical results, as well as examples where a variety of input parameters are passed.*
-->
```python
N = 10 # N evaluation instances {(x_i,y_i)}_{i=1}^N
K = 5 # K class problem
def random_mc_instance(concentration=1, onehot=False):
reference = np.argmax(
np.random.dirichlet(([concentration for _ in range(K)])), -1
) # class targets
prediction = np.random.dirichlet(([concentration for _ in range(K)])) # probabilities
if onehot:
reference = np.eye(K)[np.argmax(reference, -1)]
return reference, prediction
references, predictions = list(zip(*[random_mc_instance() for i in range(N)]))
references = np.array(references, dtype=np.int64)
predictions = np.array(predictions, dtype=np.float32)
res = ECE()._compute(predictions, references) # {'ECE': float}
```
## Limitations and Bias
<!---
*Note any known limitations or biases that the metric has, with links and references if possible.*
-->
See [3],[4] and [5].
## Citation
[1] Naeini, M.P., Cooper, G. and Hauskrecht, M., 2015, February. Obtaining well calibrated probabilities using bayesian binning. In Twenty-Ninth AAAI Conference on Artificial Intelligence.
[2] Guo, C., Pleiss, G., Sun, Y. and Weinberger, K.Q., 2017, July. On calibration of modern neural networks. In International Conference on Machine Learning (pp. 1321-1330). PMLR.
[3] Nixon, J., Dusenberry, M.W., Zhang, L., Jerfel, G. and Tran, D., 2019, June. Measuring Calibration in Deep Learning. In CVPR Workshops (Vol. 2, No. 7).
[4] Kumar, A., Liang, P.S. and Ma, T., 2019. Verified uncertainty calibration. Advances in Neural Information Processing Systems, 32.
[5] Vaicenavicius, J., Widmann, D., Andersson, C., Lindsten, F., Roll, J. and Schön, T., 2019, April. Evaluating model calibration in classification. In The 22nd International Conference on Artificial Intelligence and Statistics (pp. 3459-3467). PMLR.
[6] Allen-Zhu, Z., Li, Y. and Liang, Y., 2019. Learning and generalization in overparameterized neural networks, going beyond two layers. Advances in neural information processing systems, 32.
## Further References
<!---
*Add any useful further references.*
--> |