Document RNN (#4)
Browse files- .github/workflows/ci-cd.yml +0 -1
- .gitignore +1 -0
- docs/source/img/architecture-rnn-ltr.png +0 -0
- docs/source/img/architecture-rnn-ltr.psd +0 -0
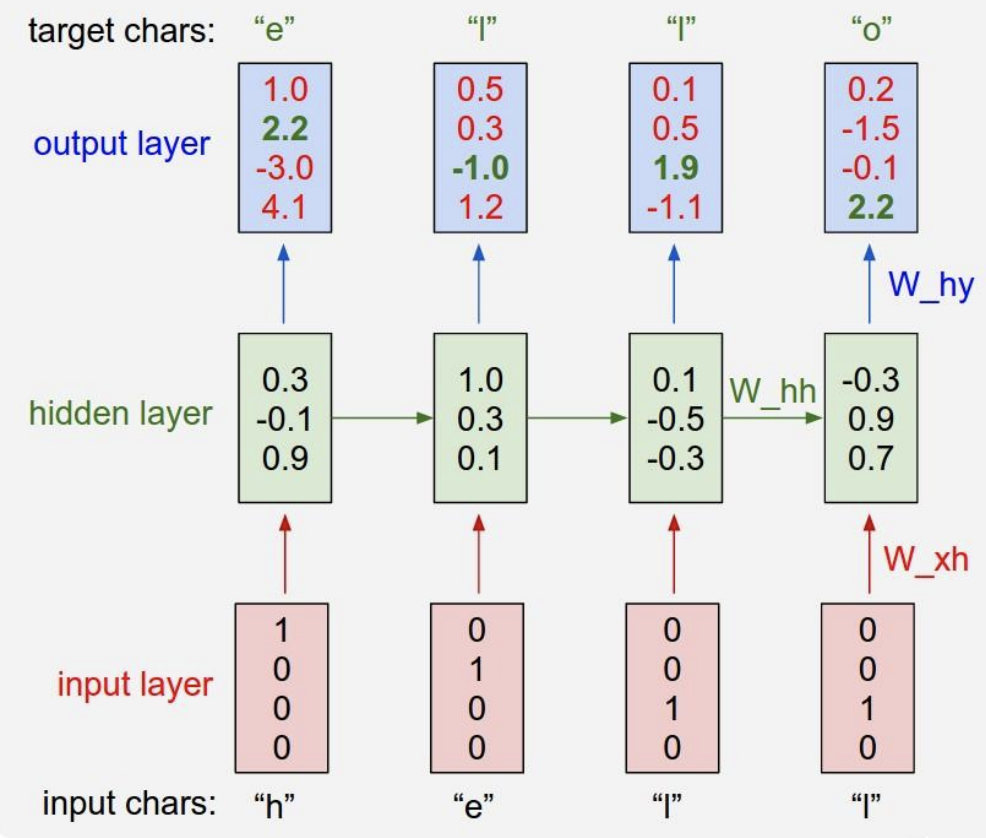
- docs/source/img/char-level-language-model.png +0 -0
- docs/source/img/description-block-rnn-ltr.png +0 -0
- docs/source/img/description-block-rnn-ltr.psd +0 -0
- docs/source/img/gradient-clipping.png +0 -0
- docs/source/img/rnn-4-black-boxes-connected.drawio +121 -0
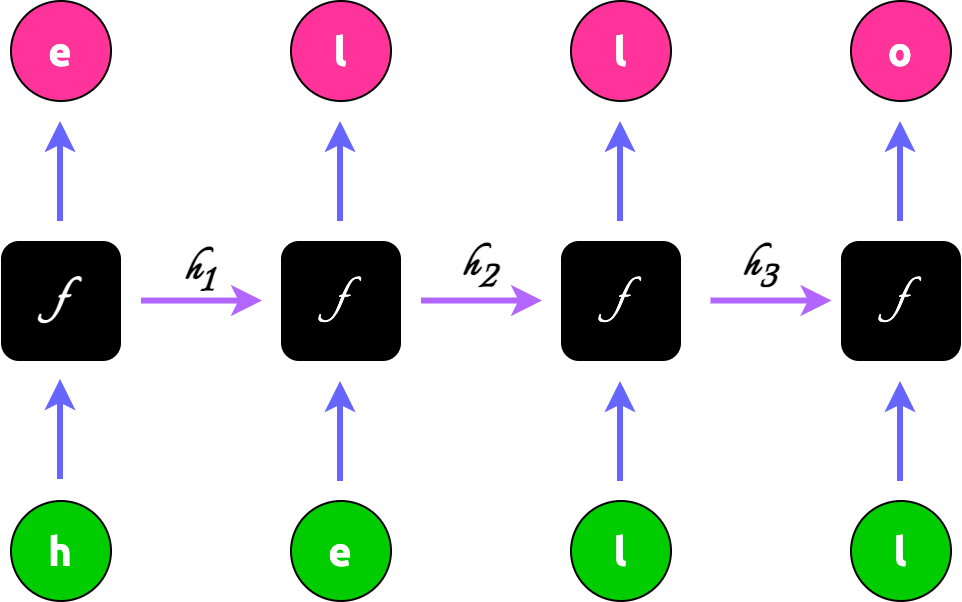
- docs/source/img/rnn-4-black-boxes-connected.png +0 -0
- docs/source/img/rnn-4-black-boxes.drawio +94 -0
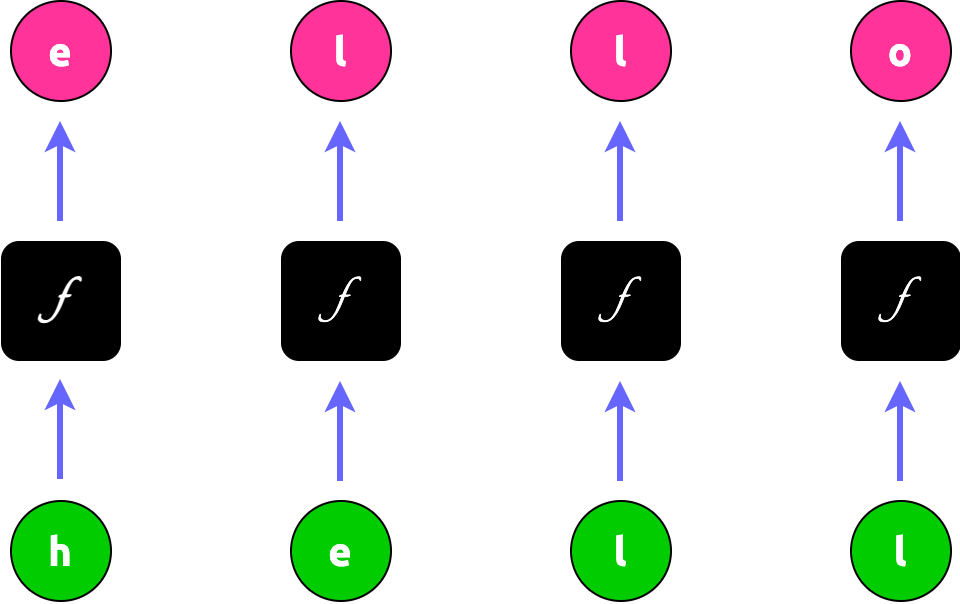
- docs/source/img/rnn-4-black-boxes.png +0 -0
- docs/source/img/rnn-multi-sequences.drawio +250 -0
- docs/source/img/rnn-multi-sequences.png +0 -0
- docs/source/img/rnn.drawio +149 -0
- docs/source/img/rnn.png +0 -0
- docs/source/lamassu.rst +1 -1
- docs/source/rnn/rnn.rst +612 -0
- docs/source/rnn/vanilla.rst +0 -176
- lamassu/rnn/example.py +50 -0
- lamassu/rnn/rnn.py +114 -0
- lamassu/rnn/vanilla.py +0 -25
- setup.py +1 -1
.github/workflows/ci-cd.yml
CHANGED
|
@@ -31,7 +31,6 @@ jobs:
|
|
| 31 |
with:
|
| 32 |
python-version: "3.10"
|
| 33 |
- name: Package up SDK
|
| 34 |
-
if: github.ref == 'refs/heads/master'
|
| 35 |
run: python setup.py sdist
|
| 36 |
- name: Publish a Python distribution to PyPI
|
| 37 |
if: github.ref == 'refs/heads/master'
|
|
|
|
| 31 |
with:
|
| 32 |
python-version: "3.10"
|
| 33 |
- name: Package up SDK
|
|
|
|
| 34 |
run: python setup.py sdist
|
| 35 |
- name: Publish a Python distribution to PyPI
|
| 36 |
if: github.ref == 'refs/heads/master'
|
.gitignore
CHANGED
|
@@ -1,2 +1,3 @@
|
|
| 1 |
.idea/
|
| 2 |
.DS_Store
|
|
|
|
|
|
| 1 |
.idea/
|
| 2 |
.DS_Store
|
| 3 |
+
__pycache__
|
docs/source/img/architecture-rnn-ltr.png
DELETED
|
Binary file (47.6 kB)
|
|
|
docs/source/img/architecture-rnn-ltr.psd
DELETED
|
Binary file (359 kB)
|
|
|
docs/source/img/char-level-language-model.png
ADDED
|
docs/source/img/description-block-rnn-ltr.png
DELETED
|
Binary file (55.5 kB)
|
|
|
docs/source/img/description-block-rnn-ltr.psd
DELETED
|
Binary file (394 kB)
|
|
|
docs/source/img/gradient-clipping.png
DELETED
|
Binary file (4.71 kB)
|
|
|
docs/source/img/rnn-4-black-boxes-connected.drawio
ADDED
|
@@ -0,0 +1,121 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
<mxfile host="app.diagrams.net" modified="2024-03-19T01:01:04.926Z" agent="Mozilla/5.0 (Macintosh; Intel Mac OS X 10_15_7) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/122.0.0.0 Safari/537.36" etag="OgWHmKqu6mVN4yDKoCwM" version="24.0.7" type="device">
|
| 2 |
+
<diagram name="Page-1" id="gxr7cFC-hZQY0lpAcxoR">
|
| 3 |
+
<mxGraphModel dx="816" dy="516" grid="1" gridSize="10" guides="1" tooltips="1" connect="1" arrows="1" fold="1" page="1" pageScale="1" pageWidth="850" pageHeight="1100" math="0" shadow="0">
|
| 4 |
+
<root>
|
| 5 |
+
<mxCell id="0" />
|
| 6 |
+
<mxCell id="1" parent="0" />
|
| 7 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-21" value="<font size="1" data-font-src="https://fonts.googleapis.com/css?family=Italianno" face="Italianno" style="" color="#ffffff"><b style="font-size: 27px;">f</b></font>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" vertex="1" parent="1">
|
| 8 |
+
<mxGeometry x="40" y="320" width="60" height="60" as="geometry" />
|
| 9 |
+
</mxCell>
|
| 10 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-22" value="<font color="#ffffff" face="Italianno" style="font-size: 27px;">f</font>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" vertex="1" parent="1">
|
| 11 |
+
<mxGeometry x="180" y="320" width="60" height="60" as="geometry" />
|
| 12 |
+
</mxCell>
|
| 13 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-23" value="<span style="color: rgb(255, 255, 255); font-family: Italianno; font-size: 27px;">f</span>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" vertex="1" parent="1">
|
| 14 |
+
<mxGeometry x="320" y="320" width="60" height="60" as="geometry" />
|
| 15 |
+
</mxCell>
|
| 16 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-24" value="<span style="color: rgb(255, 255, 255); font-family: Italianno; font-size: 27px;">f</span>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" vertex="1" parent="1">
|
| 17 |
+
<mxGeometry x="460" y="320" width="60" height="60" as="geometry" />
|
| 18 |
+
</mxCell>
|
| 19 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-25" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" edge="1" parent="1">
|
| 20 |
+
<mxGeometry relative="1" as="geometry">
|
| 21 |
+
<mxPoint x="69.5" y="439" as="sourcePoint" />
|
| 22 |
+
<mxPoint x="69.5" y="389" as="targetPoint" />
|
| 23 |
+
</mxGeometry>
|
| 24 |
+
</mxCell>
|
| 25 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-26" value="<font face="Ubuntu" style="font-size: 20px;"><b>h</b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" vertex="1" parent="1">
|
| 26 |
+
<mxGeometry x="45" y="450" width="50" height="50" as="geometry" />
|
| 27 |
+
</mxCell>
|
| 28 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-27" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" edge="1" parent="1">
|
| 29 |
+
<mxGeometry relative="1" as="geometry">
|
| 30 |
+
<mxPoint x="69.5" y="310" as="sourcePoint" />
|
| 31 |
+
<mxPoint x="69.5" y="260" as="targetPoint" />
|
| 32 |
+
</mxGeometry>
|
| 33 |
+
</mxCell>
|
| 34 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-28" value="<font face="Ubuntu"><span style="font-size: 20px;"><b>e</b></span></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" vertex="1" parent="1">
|
| 35 |
+
<mxGeometry x="45" y="200" width="50" height="50" as="geometry" />
|
| 36 |
+
</mxCell>
|
| 37 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-29" value="<font face="Ubuntu"><span style="font-size: 20px;"><b>l</b></span></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" vertex="1" parent="1">
|
| 38 |
+
<mxGeometry x="185" y="200" width="50" height="50" as="geometry" />
|
| 39 |
+
</mxCell>
|
| 40 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-30" value="<font face="Ubuntu"><span style="font-size: 20px;"><b>l</b></span></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" vertex="1" parent="1">
|
| 41 |
+
<mxGeometry x="325" y="200" width="50" height="50" as="geometry" />
|
| 42 |
+
</mxCell>
|
| 43 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-31" value="<font face="Ubuntu"><span style="font-size: 20px;"><b>o</b></span></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" vertex="1" parent="1">
|
| 44 |
+
<mxGeometry x="465" y="200" width="50" height="50" as="geometry" />
|
| 45 |
+
</mxCell>
|
| 46 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-32" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" edge="1" parent="1">
|
| 47 |
+
<mxGeometry relative="1" as="geometry">
|
| 48 |
+
<mxPoint x="209.5" y="310" as="sourcePoint" />
|
| 49 |
+
<mxPoint x="209.5" y="260" as="targetPoint" />
|
| 50 |
+
</mxGeometry>
|
| 51 |
+
</mxCell>
|
| 52 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-33" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" edge="1" parent="1">
|
| 53 |
+
<mxGeometry relative="1" as="geometry">
|
| 54 |
+
<mxPoint x="349.5" y="310" as="sourcePoint" />
|
| 55 |
+
<mxPoint x="349.5" y="260" as="targetPoint" />
|
| 56 |
+
</mxGeometry>
|
| 57 |
+
</mxCell>
|
| 58 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-34" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" edge="1" parent="1">
|
| 59 |
+
<mxGeometry relative="1" as="geometry">
|
| 60 |
+
<mxPoint x="489.5" y="310" as="sourcePoint" />
|
| 61 |
+
<mxPoint x="489.5" y="260" as="targetPoint" />
|
| 62 |
+
</mxGeometry>
|
| 63 |
+
</mxCell>
|
| 64 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-35" value="<font face="Ubuntu" style="font-size: 20px;"><b>e</b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" vertex="1" parent="1">
|
| 65 |
+
<mxGeometry x="185" y="450" width="50" height="50" as="geometry" />
|
| 66 |
+
</mxCell>
|
| 67 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-36" value="<font face="Ubuntu" style="font-size: 20px;"><b>l</b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" vertex="1" parent="1">
|
| 68 |
+
<mxGeometry x="325" y="450" width="50" height="50" as="geometry" />
|
| 69 |
+
</mxCell>
|
| 70 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-37" value="<font face="Ubuntu" style="font-size: 20px;"><b>l</b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" vertex="1" parent="1">
|
| 71 |
+
<mxGeometry x="465" y="450" width="50" height="50" as="geometry" />
|
| 72 |
+
</mxCell>
|
| 73 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-38" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" edge="1" parent="1">
|
| 74 |
+
<mxGeometry relative="1" as="geometry">
|
| 75 |
+
<mxPoint x="209.5" y="440" as="sourcePoint" />
|
| 76 |
+
<mxPoint x="209.5" y="390" as="targetPoint" />
|
| 77 |
+
</mxGeometry>
|
| 78 |
+
</mxCell>
|
| 79 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-39" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" edge="1" parent="1">
|
| 80 |
+
<mxGeometry relative="1" as="geometry">
|
| 81 |
+
<mxPoint x="349.5" y="440" as="sourcePoint" />
|
| 82 |
+
<mxPoint x="349.5" y="390" as="targetPoint" />
|
| 83 |
+
</mxGeometry>
|
| 84 |
+
</mxCell>
|
| 85 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-40" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" edge="1" parent="1">
|
| 86 |
+
<mxGeometry relative="1" as="geometry">
|
| 87 |
+
<mxPoint x="489.5" y="440" as="sourcePoint" />
|
| 88 |
+
<mxPoint x="489.5" y="390" as="targetPoint" />
|
| 89 |
+
</mxGeometry>
|
| 90 |
+
</mxCell>
|
| 91 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-44" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#B266FF;fontColor=#FF6666;" edge="1" parent="1">
|
| 92 |
+
<mxGeometry relative="1" as="geometry">
|
| 93 |
+
<mxPoint x="110" y="349.78" as="sourcePoint" />
|
| 94 |
+
<mxPoint x="170.5" y="349.78" as="targetPoint" />
|
| 95 |
+
</mxGeometry>
|
| 96 |
+
</mxCell>
|
| 97 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-45" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#B266FF;fontColor=#FF6666;" edge="1" parent="1">
|
| 98 |
+
<mxGeometry relative="1" as="geometry">
|
| 99 |
+
<mxPoint x="250" y="349.76" as="sourcePoint" />
|
| 100 |
+
<mxPoint x="310.5" y="349.76" as="targetPoint" />
|
| 101 |
+
</mxGeometry>
|
| 102 |
+
</mxCell>
|
| 103 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-46" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#B266FF;fontColor=#FF6666;" edge="1" parent="1">
|
| 104 |
+
<mxGeometry relative="1" as="geometry">
|
| 105 |
+
<mxPoint x="394.75" y="349.76" as="sourcePoint" />
|
| 106 |
+
<mxPoint x="455.25" y="349.76" as="targetPoint" />
|
| 107 |
+
</mxGeometry>
|
| 108 |
+
</mxCell>
|
| 109 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-47" value="<font data-font-src="https://fonts.googleapis.com/css?family=Italianno" face="Italianno" style="font-size: 25px;"><span style="font-size: 25px;">h<sub style="font-size: 25px;">1</sub></span></font>" style="text;html=1;align=center;verticalAlign=middle;whiteSpace=wrap;rounded=0;fontSize=25;fontStyle=1" vertex="1" parent="1">
|
| 110 |
+
<mxGeometry x="110" y="320" width="60" height="30" as="geometry" />
|
| 111 |
+
</mxCell>
|
| 112 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-48" value="<font style="font-size: 25px;"><span style="font-size: 25px;"><span style="font-size: 25px;">h</span><span style="font-size: 25px;"><sub style="font-size: 25px;">2</sub></span></span></font>" style="text;html=1;align=center;verticalAlign=middle;whiteSpace=wrap;rounded=0;fontFamily=Italianno;fontSource=https%3A%2F%2Ffonts.googleapis.com%2Fcss%3Ffamily%3DItalianno;fontSize=25;fontStyle=1" vertex="1" parent="1">
|
| 113 |
+
<mxGeometry x="250" y="320" width="60" height="30" as="geometry" />
|
| 114 |
+
</mxCell>
|
| 115 |
+
<mxCell id="o5WZRm4PuDRFcwwRBSCM-49" value="<font style="font-size: 25px;"><span style="font-size: 25px;"><span style="font-size: 25px;">h</span><span style="font-size: 25px;"><sub style="font-size: 25px;">3</sub></span></span></font>" style="text;html=1;align=center;verticalAlign=middle;whiteSpace=wrap;rounded=0;fontFamily=Italianno;fontSource=https%3A%2F%2Ffonts.googleapis.com%2Fcss%3Ffamily%3DItalianno;fontSize=25;fontStyle=1" vertex="1" parent="1">
|
| 116 |
+
<mxGeometry x="390" y="320" width="60" height="30" as="geometry" />
|
| 117 |
+
</mxCell>
|
| 118 |
+
</root>
|
| 119 |
+
</mxGraphModel>
|
| 120 |
+
</diagram>
|
| 121 |
+
</mxfile>
|
docs/source/img/rnn-4-black-boxes-connected.png
ADDED
|
docs/source/img/rnn-4-black-boxes.drawio
ADDED
|
@@ -0,0 +1,94 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
<mxfile host="app.diagrams.net" modified="2024-03-19T00:55:52.180Z" agent="Mozilla/5.0 (Macintosh; Intel Mac OS X 10_15_7) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/122.0.0.0 Safari/537.36" etag="0mAcZEyuQtVV9Bg2w-Tf" version="24.0.7" type="device">
|
| 2 |
+
<diagram name="Page-1" id="DUD_6-T85kScICrpKMMz">
|
| 3 |
+
<mxGraphModel dx="1536" dy="972" grid="1" gridSize="10" guides="1" tooltips="1" connect="1" arrows="1" fold="1" page="1" pageScale="1" pageWidth="850" pageHeight="1100" math="0" shadow="0">
|
| 4 |
+
<root>
|
| 5 |
+
<mxCell id="0" />
|
| 6 |
+
<mxCell id="1" parent="0" />
|
| 7 |
+
<mxCell id="LGyqkTtVOXbUGTZdzTyq-1" value="<font size="1" data-font-src="https://fonts.googleapis.com/css?family=Italianno" face="Italianno" style="" color="#ffffff"><b style="font-size: 27px;">f</b></font>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" parent="1" vertex="1">
|
| 8 |
+
<mxGeometry x="20" y="300" width="60" height="60" as="geometry" />
|
| 9 |
+
</mxCell>
|
| 10 |
+
<mxCell id="LGyqkTtVOXbUGTZdzTyq-2" value="<font color="#ffffff" face="Italianno" style="font-size: 27px;">f</font>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" parent="1" vertex="1">
|
| 11 |
+
<mxGeometry x="160" y="300" width="60" height="60" as="geometry" />
|
| 12 |
+
</mxCell>
|
| 13 |
+
<mxCell id="LGyqkTtVOXbUGTZdzTyq-4" value="<span style="color: rgb(255, 255, 255); font-family: Italianno; font-size: 27px;">f</span>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" parent="1" vertex="1">
|
| 14 |
+
<mxGeometry x="300" y="300" width="60" height="60" as="geometry" />
|
| 15 |
+
</mxCell>
|
| 16 |
+
<mxCell id="LGyqkTtVOXbUGTZdzTyq-5" value="<span style="color: rgb(255, 255, 255); font-family: Italianno; font-size: 27px;">f</span>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" parent="1" vertex="1">
|
| 17 |
+
<mxGeometry x="440" y="300" width="60" height="60" as="geometry" />
|
| 18 |
+
</mxCell>
|
| 19 |
+
<mxCell id="LGyqkTtVOXbUGTZdzTyq-11" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 20 |
+
<mxGeometry relative="1" as="geometry">
|
| 21 |
+
<mxPoint x="49.5" y="419" as="sourcePoint" />
|
| 22 |
+
<mxPoint x="49.5" y="369" as="targetPoint" />
|
| 23 |
+
</mxGeometry>
|
| 24 |
+
</mxCell>
|
| 25 |
+
<mxCell id="hK792VXiPIr8ubialXFB-1" value="<font face="Ubuntu" style="font-size: 20px;"><b>h</b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" vertex="1" parent="1">
|
| 26 |
+
<mxGeometry x="25" y="430" width="50" height="50" as="geometry" />
|
| 27 |
+
</mxCell>
|
| 28 |
+
<mxCell id="hK792VXiPIr8ubialXFB-2" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" edge="1" parent="1">
|
| 29 |
+
<mxGeometry relative="1" as="geometry">
|
| 30 |
+
<mxPoint x="49.5" y="290" as="sourcePoint" />
|
| 31 |
+
<mxPoint x="49.5" y="240" as="targetPoint" />
|
| 32 |
+
</mxGeometry>
|
| 33 |
+
</mxCell>
|
| 34 |
+
<mxCell id="hK792VXiPIr8ubialXFB-3" value="<font face="Ubuntu"><span style="font-size: 20px;"><b>e</b></span></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" vertex="1" parent="1">
|
| 35 |
+
<mxGeometry x="25" y="180" width="50" height="50" as="geometry" />
|
| 36 |
+
</mxCell>
|
| 37 |
+
<mxCell id="hK792VXiPIr8ubialXFB-4" value="<font face="Ubuntu"><span style="font-size: 20px;"><b>l</b></span></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" vertex="1" parent="1">
|
| 38 |
+
<mxGeometry x="165" y="180" width="50" height="50" as="geometry" />
|
| 39 |
+
</mxCell>
|
| 40 |
+
<mxCell id="hK792VXiPIr8ubialXFB-5" value="<font face="Ubuntu"><span style="font-size: 20px;"><b>l</b></span></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" vertex="1" parent="1">
|
| 41 |
+
<mxGeometry x="305" y="180" width="50" height="50" as="geometry" />
|
| 42 |
+
</mxCell>
|
| 43 |
+
<mxCell id="hK792VXiPIr8ubialXFB-6" value="<font face="Ubuntu"><span style="font-size: 20px;"><b>o</b></span></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" vertex="1" parent="1">
|
| 44 |
+
<mxGeometry x="445" y="180" width="50" height="50" as="geometry" />
|
| 45 |
+
</mxCell>
|
| 46 |
+
<mxCell id="hK792VXiPIr8ubialXFB-8" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" edge="1" parent="1">
|
| 47 |
+
<mxGeometry relative="1" as="geometry">
|
| 48 |
+
<mxPoint x="189.5" y="290" as="sourcePoint" />
|
| 49 |
+
<mxPoint x="189.5" y="240" as="targetPoint" />
|
| 50 |
+
</mxGeometry>
|
| 51 |
+
</mxCell>
|
| 52 |
+
<mxCell id="hK792VXiPIr8ubialXFB-9" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" edge="1" parent="1">
|
| 53 |
+
<mxGeometry relative="1" as="geometry">
|
| 54 |
+
<mxPoint x="329.5" y="290" as="sourcePoint" />
|
| 55 |
+
<mxPoint x="329.5" y="240" as="targetPoint" />
|
| 56 |
+
</mxGeometry>
|
| 57 |
+
</mxCell>
|
| 58 |
+
<mxCell id="hK792VXiPIr8ubialXFB-10" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" edge="1" parent="1">
|
| 59 |
+
<mxGeometry relative="1" as="geometry">
|
| 60 |
+
<mxPoint x="469.5" y="290" as="sourcePoint" />
|
| 61 |
+
<mxPoint x="469.5" y="240" as="targetPoint" />
|
| 62 |
+
</mxGeometry>
|
| 63 |
+
</mxCell>
|
| 64 |
+
<mxCell id="hK792VXiPIr8ubialXFB-11" value="<font face="Ubuntu" style="font-size: 20px;"><b>e</b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" vertex="1" parent="1">
|
| 65 |
+
<mxGeometry x="165" y="430" width="50" height="50" as="geometry" />
|
| 66 |
+
</mxCell>
|
| 67 |
+
<mxCell id="hK792VXiPIr8ubialXFB-12" value="<font face="Ubuntu" style="font-size: 20px;"><b>l</b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" vertex="1" parent="1">
|
| 68 |
+
<mxGeometry x="305" y="430" width="50" height="50" as="geometry" />
|
| 69 |
+
</mxCell>
|
| 70 |
+
<mxCell id="hK792VXiPIr8ubialXFB-13" value="<font face="Ubuntu" style="font-size: 20px;"><b>l</b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" vertex="1" parent="1">
|
| 71 |
+
<mxGeometry x="445" y="430" width="50" height="50" as="geometry" />
|
| 72 |
+
</mxCell>
|
| 73 |
+
<mxCell id="hK792VXiPIr8ubialXFB-14" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" edge="1" parent="1">
|
| 74 |
+
<mxGeometry relative="1" as="geometry">
|
| 75 |
+
<mxPoint x="189.5" y="420" as="sourcePoint" />
|
| 76 |
+
<mxPoint x="189.5" y="370" as="targetPoint" />
|
| 77 |
+
</mxGeometry>
|
| 78 |
+
</mxCell>
|
| 79 |
+
<mxCell id="hK792VXiPIr8ubialXFB-15" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" edge="1" parent="1">
|
| 80 |
+
<mxGeometry relative="1" as="geometry">
|
| 81 |
+
<mxPoint x="329.5" y="420" as="sourcePoint" />
|
| 82 |
+
<mxPoint x="329.5" y="370" as="targetPoint" />
|
| 83 |
+
</mxGeometry>
|
| 84 |
+
</mxCell>
|
| 85 |
+
<mxCell id="hK792VXiPIr8ubialXFB-16" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" edge="1" parent="1">
|
| 86 |
+
<mxGeometry relative="1" as="geometry">
|
| 87 |
+
<mxPoint x="469.5" y="420" as="sourcePoint" />
|
| 88 |
+
<mxPoint x="469.5" y="370" as="targetPoint" />
|
| 89 |
+
</mxGeometry>
|
| 90 |
+
</mxCell>
|
| 91 |
+
</root>
|
| 92 |
+
</mxGraphModel>
|
| 93 |
+
</diagram>
|
| 94 |
+
</mxfile>
|
docs/source/img/rnn-4-black-boxes.png
ADDED
|
docs/source/img/rnn-multi-sequences.drawio
ADDED
|
@@ -0,0 +1,250 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
<mxfile host="app.diagrams.net" modified="2024-03-19T01:28:19.045Z" agent="Mozilla/5.0 (Macintosh; Intel Mac OS X 10_15_7) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/122.0.0.0 Safari/537.36" etag="1-yK62UkPGlKoTsEWqch" version="24.0.7" type="device">
|
| 2 |
+
<diagram name="Page-1" id="6HRoGfWBaaDKhnXAU6vd">
|
| 3 |
+
<mxGraphModel dx="2156" dy="1926" grid="1" gridSize="10" guides="1" tooltips="1" connect="1" arrows="1" fold="1" page="1" pageScale="1" pageWidth="850" pageHeight="1100" math="0" shadow="0">
|
| 4 |
+
<root>
|
| 5 |
+
<mxCell id="0" />
|
| 6 |
+
<mxCell id="1" parent="0" />
|
| 7 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-1" value="<font size="1" data-font-src="https://fonts.googleapis.com/css?family=Italianno" face="Italianno" style="" color="#ffffff"><b style="font-size: 27px;">f</b></font>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" parent="1" vertex="1">
|
| 8 |
+
<mxGeometry x="40" y="320" width="60" height="60" as="geometry" />
|
| 9 |
+
</mxCell>
|
| 10 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-2" value="<font color="#ffffff" face="Italianno" style="font-size: 27px;">f</font>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" parent="1" vertex="1">
|
| 11 |
+
<mxGeometry x="180" y="320" width="60" height="60" as="geometry" />
|
| 12 |
+
</mxCell>
|
| 13 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-3" value="<span style="color: rgb(255, 255, 255); font-family: Italianno; font-size: 27px;">f</span>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" parent="1" vertex="1">
|
| 14 |
+
<mxGeometry x="320" y="320" width="60" height="60" as="geometry" />
|
| 15 |
+
</mxCell>
|
| 16 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-4" value="<span style="color: rgb(255, 255, 255); font-family: Italianno; font-size: 27px;">f</span>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" parent="1" vertex="1">
|
| 17 |
+
<mxGeometry x="460" y="320" width="60" height="60" as="geometry" />
|
| 18 |
+
</mxCell>
|
| 19 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-5" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 20 |
+
<mxGeometry relative="1" as="geometry">
|
| 21 |
+
<mxPoint x="69.5" y="439" as="sourcePoint" />
|
| 22 |
+
<mxPoint x="69.5" y="389" as="targetPoint" />
|
| 23 |
+
</mxGeometry>
|
| 24 |
+
</mxCell>
|
| 25 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-6" value="<font face="Ubuntu" style="font-size: 20px;"><b>h</b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 26 |
+
<mxGeometry x="45" y="450" width="50" height="50" as="geometry" />
|
| 27 |
+
</mxCell>
|
| 28 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-7" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 29 |
+
<mxGeometry relative="1" as="geometry">
|
| 30 |
+
<mxPoint x="69.5" y="310" as="sourcePoint" />
|
| 31 |
+
<mxPoint x="69.5" y="260" as="targetPoint" />
|
| 32 |
+
</mxGeometry>
|
| 33 |
+
</mxCell>
|
| 34 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-8" value="<font face="Ubuntu"><span style="font-size: 20px;"><b>e</b></span></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 35 |
+
<mxGeometry x="45" y="200" width="50" height="50" as="geometry" />
|
| 36 |
+
</mxCell>
|
| 37 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-9" value="<font face="Ubuntu"><span style="font-size: 20px;"><b>l</b></span></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 38 |
+
<mxGeometry x="185" y="200" width="50" height="50" as="geometry" />
|
| 39 |
+
</mxCell>
|
| 40 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-10" value="<font face="Ubuntu"><span style="font-size: 20px;"><b>l</b></span></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 41 |
+
<mxGeometry x="325" y="200" width="50" height="50" as="geometry" />
|
| 42 |
+
</mxCell>
|
| 43 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-11" value="<font face="Ubuntu"><span style="font-size: 20px;"><b>o</b></span></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 44 |
+
<mxGeometry x="465" y="200" width="50" height="50" as="geometry" />
|
| 45 |
+
</mxCell>
|
| 46 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-12" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 47 |
+
<mxGeometry relative="1" as="geometry">
|
| 48 |
+
<mxPoint x="209.5" y="310" as="sourcePoint" />
|
| 49 |
+
<mxPoint x="209.5" y="260" as="targetPoint" />
|
| 50 |
+
</mxGeometry>
|
| 51 |
+
</mxCell>
|
| 52 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-13" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 53 |
+
<mxGeometry relative="1" as="geometry">
|
| 54 |
+
<mxPoint x="349.5" y="310" as="sourcePoint" />
|
| 55 |
+
<mxPoint x="349.5" y="260" as="targetPoint" />
|
| 56 |
+
</mxGeometry>
|
| 57 |
+
</mxCell>
|
| 58 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-14" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 59 |
+
<mxGeometry relative="1" as="geometry">
|
| 60 |
+
<mxPoint x="489.5" y="310" as="sourcePoint" />
|
| 61 |
+
<mxPoint x="489.5" y="260" as="targetPoint" />
|
| 62 |
+
</mxGeometry>
|
| 63 |
+
</mxCell>
|
| 64 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-15" value="<font face="Ubuntu" style="font-size: 20px;"><b>e</b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 65 |
+
<mxGeometry x="185" y="450" width="50" height="50" as="geometry" />
|
| 66 |
+
</mxCell>
|
| 67 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-16" value="<font face="Ubuntu" style="font-size: 20px;"><b>l</b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 68 |
+
<mxGeometry x="325" y="450" width="50" height="50" as="geometry" />
|
| 69 |
+
</mxCell>
|
| 70 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-17" value="<font face="Ubuntu" style="font-size: 20px;"><b>l</b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 71 |
+
<mxGeometry x="465" y="450" width="50" height="50" as="geometry" />
|
| 72 |
+
</mxCell>
|
| 73 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-18" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 74 |
+
<mxGeometry relative="1" as="geometry">
|
| 75 |
+
<mxPoint x="209.5" y="440" as="sourcePoint" />
|
| 76 |
+
<mxPoint x="209.5" y="390" as="targetPoint" />
|
| 77 |
+
</mxGeometry>
|
| 78 |
+
</mxCell>
|
| 79 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-19" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 80 |
+
<mxGeometry relative="1" as="geometry">
|
| 81 |
+
<mxPoint x="349.5" y="440" as="sourcePoint" />
|
| 82 |
+
<mxPoint x="349.5" y="390" as="targetPoint" />
|
| 83 |
+
</mxGeometry>
|
| 84 |
+
</mxCell>
|
| 85 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-20" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 86 |
+
<mxGeometry relative="1" as="geometry">
|
| 87 |
+
<mxPoint x="489.5" y="440" as="sourcePoint" />
|
| 88 |
+
<mxPoint x="489.5" y="390" as="targetPoint" />
|
| 89 |
+
</mxGeometry>
|
| 90 |
+
</mxCell>
|
| 91 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-21" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#B266FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 92 |
+
<mxGeometry relative="1" as="geometry">
|
| 93 |
+
<mxPoint x="110" y="349.78" as="sourcePoint" />
|
| 94 |
+
<mxPoint x="170.5" y="349.78" as="targetPoint" />
|
| 95 |
+
</mxGeometry>
|
| 96 |
+
</mxCell>
|
| 97 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-22" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#B266FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 98 |
+
<mxGeometry relative="1" as="geometry">
|
| 99 |
+
<mxPoint x="250" y="349.76" as="sourcePoint" />
|
| 100 |
+
<mxPoint x="310.5" y="349.76" as="targetPoint" />
|
| 101 |
+
</mxGeometry>
|
| 102 |
+
</mxCell>
|
| 103 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-23" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#B266FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 104 |
+
<mxGeometry relative="1" as="geometry">
|
| 105 |
+
<mxPoint x="394.75" y="349.76" as="sourcePoint" />
|
| 106 |
+
<mxPoint x="455.25" y="349.76" as="targetPoint" />
|
| 107 |
+
</mxGeometry>
|
| 108 |
+
</mxCell>
|
| 109 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-24" value="<font data-font-src="https://fonts.googleapis.com/css?family=Italianno" face="Italianno" style="font-size: 25px;"><span style="font-size: 25px;">h<sub style="font-size: 25px;">1</sub></span></font>" style="text;html=1;align=center;verticalAlign=middle;whiteSpace=wrap;rounded=0;fontSize=25;fontStyle=1" parent="1" vertex="1">
|
| 110 |
+
<mxGeometry x="110" y="320" width="60" height="30" as="geometry" />
|
| 111 |
+
</mxCell>
|
| 112 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-25" value="<font style="font-size: 25px;"><span style="font-size: 25px;"><span style="font-size: 25px;">h</span><span style="font-size: 25px;"><sub style="font-size: 25px;">2</sub></span></span></font>" style="text;html=1;align=center;verticalAlign=middle;whiteSpace=wrap;rounded=0;fontFamily=Italianno;fontSource=https%3A%2F%2Ffonts.googleapis.com%2Fcss%3Ffamily%3DItalianno;fontSize=25;fontStyle=1" parent="1" vertex="1">
|
| 113 |
+
<mxGeometry x="250" y="320" width="60" height="30" as="geometry" />
|
| 114 |
+
</mxCell>
|
| 115 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-26" value="<font style="font-size: 25px;"><span style="font-size: 25px;"><span style="font-size: 25px;">h</span><span style="font-size: 25px;"><sub style="font-size: 25px;">3</sub></span></span></font>" style="text;html=1;align=center;verticalAlign=middle;whiteSpace=wrap;rounded=0;fontFamily=Italianno;fontSource=https%3A%2F%2Ffonts.googleapis.com%2Fcss%3Ffamily%3DItalianno;fontSize=25;fontStyle=1" parent="1" vertex="1">
|
| 116 |
+
<mxGeometry x="390" y="320" width="60" height="30" as="geometry" />
|
| 117 |
+
</mxCell>
|
| 118 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-27" value="<font face="Ubuntu" size="1" style="" color="#ffffff"><b style="font-size: 23px;">RNN</b></font>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" parent="1" vertex="1">
|
| 119 |
+
<mxGeometry x="-140" y="320" width="60" height="60" as="geometry" />
|
| 120 |
+
</mxCell>
|
| 121 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-28" value="<font face="Ubuntu" style="font-size: 20px;"><b>hell</b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 122 |
+
<mxGeometry x="-135" y="450" width="50" height="50" as="geometry" />
|
| 123 |
+
</mxCell>
|
| 124 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-29" value="<font face="Ubuntu"><span style="font-size: 20px;"><b>ello</b></span></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 125 |
+
<mxGeometry x="-135" y="200" width="50" height="50" as="geometry" />
|
| 126 |
+
</mxCell>
|
| 127 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-30" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 128 |
+
<mxGeometry relative="1" as="geometry">
|
| 129 |
+
<mxPoint x="-110.25999999999999" y="310" as="sourcePoint" />
|
| 130 |
+
<mxPoint x="-110.25999999999999" y="260" as="targetPoint" />
|
| 131 |
+
</mxGeometry>
|
| 132 |
+
</mxCell>
|
| 133 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-31" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 134 |
+
<mxGeometry relative="1" as="geometry">
|
| 135 |
+
<mxPoint x="-110.25999999999999" y="440" as="sourcePoint" />
|
| 136 |
+
<mxPoint x="-110.25999999999999" y="390" as="targetPoint" />
|
| 137 |
+
</mxGeometry>
|
| 138 |
+
</mxCell>
|
| 139 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-33" value="" style="shape=flexArrow;endArrow=classic;html=1;rounded=0;strokeWidth=3;" parent="1" edge="1">
|
| 140 |
+
<mxGeometry width="50" height="50" relative="1" as="geometry">
|
| 141 |
+
<mxPoint x="-70" y="350" as="sourcePoint" />
|
| 142 |
+
<mxPoint x="30" y="350" as="targetPoint" />
|
| 143 |
+
</mxGeometry>
|
| 144 |
+
</mxCell>
|
| 145 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-34" value="<b><font style="font-size: 19px;" face="Ubuntu">Unfold</font></b>" style="text;html=1;align=center;verticalAlign=middle;whiteSpace=wrap;rounded=0;" parent="1" vertex="1">
|
| 146 |
+
<mxGeometry x="-50" y="290" width="60" height="30" as="geometry" />
|
| 147 |
+
</mxCell>
|
| 148 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-35" value="<font size="1" data-font-src="https://fonts.googleapis.com/css?family=Italianno" face="Italianno" style="" color="#ffffff"><b style="font-size: 27px;">f</b></font>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" parent="1" vertex="1">
|
| 149 |
+
<mxGeometry x="40" y="-50" width="60" height="60" as="geometry" />
|
| 150 |
+
</mxCell>
|
| 151 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-36" value="<font color="#ffffff" face="Italianno" style="font-size: 27px;">f</font>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" parent="1" vertex="1">
|
| 152 |
+
<mxGeometry x="180" y="-50" width="60" height="60" as="geometry" />
|
| 153 |
+
</mxCell>
|
| 154 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-37" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 155 |
+
<mxGeometry relative="1" as="geometry">
|
| 156 |
+
<mxPoint x="69.5" y="69" as="sourcePoint" />
|
| 157 |
+
<mxPoint x="69.5" y="19" as="targetPoint" />
|
| 158 |
+
</mxGeometry>
|
| 159 |
+
</mxCell>
|
| 160 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-38" value="<font face="Ubuntu" style="font-size: 20px;"><b>c</b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 161 |
+
<mxGeometry x="45" y="80" width="50" height="50" as="geometry" />
|
| 162 |
+
</mxCell>
|
| 163 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-39" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 164 |
+
<mxGeometry relative="1" as="geometry">
|
| 165 |
+
<mxPoint x="69.5" y="-60" as="sourcePoint" />
|
| 166 |
+
<mxPoint x="69.5" y="-110" as="targetPoint" />
|
| 167 |
+
</mxGeometry>
|
| 168 |
+
</mxCell>
|
| 169 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-40" value="<font face="Ubuntu"><span style="font-size: 20px;"><b>a</b></span></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 170 |
+
<mxGeometry x="45" y="-170" width="50" height="50" as="geometry" />
|
| 171 |
+
</mxCell>
|
| 172 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-41" value="<font face="Ubuntu"><span style="font-size: 20px;"><b>t</b></span></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 173 |
+
<mxGeometry x="185" y="-170" width="50" height="50" as="geometry" />
|
| 174 |
+
</mxCell>
|
| 175 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-42" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 176 |
+
<mxGeometry relative="1" as="geometry">
|
| 177 |
+
<mxPoint x="209.5" y="-60" as="sourcePoint" />
|
| 178 |
+
<mxPoint x="209.5" y="-110" as="targetPoint" />
|
| 179 |
+
</mxGeometry>
|
| 180 |
+
</mxCell>
|
| 181 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-43" value="<font face="Ubuntu" style="font-size: 20px;"><b>a</b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 182 |
+
<mxGeometry x="185" y="80" width="50" height="50" as="geometry" />
|
| 183 |
+
</mxCell>
|
| 184 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-44" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 185 |
+
<mxGeometry relative="1" as="geometry">
|
| 186 |
+
<mxPoint x="209.5" y="70" as="sourcePoint" />
|
| 187 |
+
<mxPoint x="209.5" y="20" as="targetPoint" />
|
| 188 |
+
</mxGeometry>
|
| 189 |
+
</mxCell>
|
| 190 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-45" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#B266FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 191 |
+
<mxGeometry relative="1" as="geometry">
|
| 192 |
+
<mxPoint x="110" y="-20.220000000000027" as="sourcePoint" />
|
| 193 |
+
<mxPoint x="170.5" y="-20.220000000000027" as="targetPoint" />
|
| 194 |
+
</mxGeometry>
|
| 195 |
+
</mxCell>
|
| 196 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-46" value="<font data-font-src="https://fonts.googleapis.com/css?family=Italianno" face="Italianno" style="font-size: 25px;"><span style="font-size: 25px;">h<sub style="font-size: 25px;">1</sub></span></font>" style="text;html=1;align=center;verticalAlign=middle;whiteSpace=wrap;rounded=0;fontSize=25;fontStyle=1" parent="1" vertex="1">
|
| 197 |
+
<mxGeometry x="110" y="-50" width="60" height="30" as="geometry" />
|
| 198 |
+
</mxCell>
|
| 199 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-47" value="<font face="Ubuntu" size="1" style="" color="#ffffff"><b style="font-size: 23px;">RNN</b></font>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" parent="1" vertex="1">
|
| 200 |
+
<mxGeometry x="-140" y="-50" width="60" height="60" as="geometry" />
|
| 201 |
+
</mxCell>
|
| 202 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-48" value="<font face="Ubuntu" style="font-size: 20px;"><b>ca</b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 203 |
+
<mxGeometry x="-135" y="80" width="50" height="50" as="geometry" />
|
| 204 |
+
</mxCell>
|
| 205 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-49" value="<font face="Ubuntu"><span style="font-size: 20px;"><b>at</b></span></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 206 |
+
<mxGeometry x="-135" y="-170" width="50" height="50" as="geometry" />
|
| 207 |
+
</mxCell>
|
| 208 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-50" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 209 |
+
<mxGeometry relative="1" as="geometry">
|
| 210 |
+
<mxPoint x="-110.25999999999999" y="-60" as="sourcePoint" />
|
| 211 |
+
<mxPoint x="-110.25999999999999" y="-110" as="targetPoint" />
|
| 212 |
+
</mxGeometry>
|
| 213 |
+
</mxCell>
|
| 214 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-51" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 215 |
+
<mxGeometry relative="1" as="geometry">
|
| 216 |
+
<mxPoint x="-110.25999999999999" y="70" as="sourcePoint" />
|
| 217 |
+
<mxPoint x="-110.25999999999999" y="20" as="targetPoint" />
|
| 218 |
+
</mxGeometry>
|
| 219 |
+
</mxCell>
|
| 220 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-53" value="" style="shape=flexArrow;endArrow=classic;html=1;rounded=0;strokeWidth=3;" parent="1" edge="1">
|
| 221 |
+
<mxGeometry width="50" height="50" relative="1" as="geometry">
|
| 222 |
+
<mxPoint x="-70" y="-20" as="sourcePoint" />
|
| 223 |
+
<mxPoint x="30" y="-20" as="targetPoint" />
|
| 224 |
+
</mxGeometry>
|
| 225 |
+
</mxCell>
|
| 226 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-54" value="<b><font style="font-size: 19px;" face="Ubuntu">Unfold</font></b>" style="text;html=1;align=center;verticalAlign=middle;whiteSpace=wrap;rounded=0;" parent="1" vertex="1">
|
| 227 |
+
<mxGeometry x="-50" y="-80" width="60" height="30" as="geometry" />
|
| 228 |
+
</mxCell>
|
| 229 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-55" value="" style="endArrow=none;dashed=1;html=1;dashPattern=1 3;strokeWidth=3;rounded=0;" parent="1" edge="1">
|
| 230 |
+
<mxGeometry width="50" height="50" relative="1" as="geometry">
|
| 231 |
+
<mxPoint x="-225" y="104.82000000000001" as="sourcePoint" />
|
| 232 |
+
<mxPoint x="-150" y="105.18" as="targetPoint" />
|
| 233 |
+
</mxGeometry>
|
| 234 |
+
</mxCell>
|
| 235 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-56" value="" style="endArrow=none;dashed=1;html=1;dashPattern=1 3;strokeWidth=3;rounded=0;" parent="1" edge="1">
|
| 236 |
+
<mxGeometry width="50" height="50" relative="1" as="geometry">
|
| 237 |
+
<mxPoint x="-240" y="474.63" as="sourcePoint" />
|
| 238 |
+
<mxPoint x="-165" y="474.99" as="targetPoint" />
|
| 239 |
+
</mxGeometry>
|
| 240 |
+
</mxCell>
|
| 241 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-57" value="<b><font style="font-size: 19px;" face="Ubuntu">sequence 1</font></b>" style="text;html=1;align=center;verticalAlign=middle;whiteSpace=wrap;rounded=0;" parent="1" vertex="1">
|
| 242 |
+
<mxGeometry x="-345" y="90" width="110" height="30" as="geometry" />
|
| 243 |
+
</mxCell>
|
| 244 |
+
<mxCell id="vckTE8xcX2gjwNGocpAb-58" value="<b><font style="font-size: 19px;" face="Ubuntu">sequence 2</font></b>" style="text;html=1;align=center;verticalAlign=middle;whiteSpace=wrap;rounded=0;" parent="1" vertex="1">
|
| 245 |
+
<mxGeometry x="-360" y="460" width="110" height="30" as="geometry" />
|
| 246 |
+
</mxCell>
|
| 247 |
+
</root>
|
| 248 |
+
</mxGraphModel>
|
| 249 |
+
</diagram>
|
| 250 |
+
</mxfile>
|
docs/source/img/rnn-multi-sequences.png
ADDED

|
docs/source/img/rnn.drawio
ADDED
|
@@ -0,0 +1,149 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
<mxfile host="app.diagrams.net" modified="2024-03-19T01:41:00.069Z" agent="Mozilla/5.0 (Macintosh; Intel Mac OS X 10_15_7) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/122.0.0.0 Safari/537.36" etag="gBXA4TJMJ-xFoxQL8in4" version="24.0.7" type="device">
|
| 2 |
+
<diagram name="Page-1" id="DUD_6-T85kScICrpKMMz">
|
| 3 |
+
<mxGraphModel dx="1783" dy="590" grid="1" gridSize="10" guides="1" tooltips="1" connect="1" arrows="1" fold="1" page="1" pageScale="1" pageWidth="850" pageHeight="1100" math="0" shadow="0">
|
| 4 |
+
<root>
|
| 5 |
+
<mxCell id="0" />
|
| 6 |
+
<mxCell id="1" parent="0" />
|
| 7 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-1" value="<font size="1" data-font-src="https://fonts.googleapis.com/css?family=Italianno" face="Italianno" style="" color="#ffffff"><b style="font-size: 27px;">f</b></font>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" parent="1" vertex="1">
|
| 8 |
+
<mxGeometry x="40" y="320" width="60" height="60" as="geometry" />
|
| 9 |
+
</mxCell>
|
| 10 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-2" value="<font color="#ffffff" face="Italianno" style="font-size: 27px;">f</font>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" parent="1" vertex="1">
|
| 11 |
+
<mxGeometry x="180" y="320" width="60" height="60" as="geometry" />
|
| 12 |
+
</mxCell>
|
| 13 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-4" value="<span style="color: rgb(255, 255, 255); font-family: Italianno; font-size: 27px;">f</span>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" parent="1" vertex="1">
|
| 14 |
+
<mxGeometry x="460" y="320" width="60" height="60" as="geometry" />
|
| 15 |
+
</mxCell>
|
| 16 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-5" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 17 |
+
<mxGeometry relative="1" as="geometry">
|
| 18 |
+
<mxPoint x="69.5" y="439" as="sourcePoint" />
|
| 19 |
+
<mxPoint x="69.5" y="389" as="targetPoint" />
|
| 20 |
+
</mxGeometry>
|
| 21 |
+
</mxCell>
|
| 22 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-6" value="<font face="Ubuntu" style="font-size: 20px;"><b>x<sub>1</sub></b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 23 |
+
<mxGeometry x="45" y="450" width="50" height="50" as="geometry" />
|
| 24 |
+
</mxCell>
|
| 25 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-7" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 26 |
+
<mxGeometry relative="1" as="geometry">
|
| 27 |
+
<mxPoint x="69.5" y="310" as="sourcePoint" />
|
| 28 |
+
<mxPoint x="69.5" y="260" as="targetPoint" />
|
| 29 |
+
</mxGeometry>
|
| 30 |
+
</mxCell>
|
| 31 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-8" value="<font face="Ubuntu"><span style="font-size: 20px;"><b>o<sub>1</sub></b></span></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 32 |
+
<mxGeometry x="45" y="200" width="50" height="50" as="geometry" />
|
| 33 |
+
</mxCell>
|
| 34 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-9" value="<b style="font-family: Ubuntu; font-size: 20px;">o</b><b style="font-family: Ubuntu; font-size: 16.6667px;"><sub>2</sub></b>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 35 |
+
<mxGeometry x="185" y="200" width="50" height="50" as="geometry" />
|
| 36 |
+
</mxCell>
|
| 37 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-11" value="<b style="font-family: Ubuntu; font-size: 20px;">o</b><b style="font-family: Ubuntu; font-size: 13.8889px;">n</b>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 38 |
+
<mxGeometry x="465" y="200" width="50" height="50" as="geometry" />
|
| 39 |
+
</mxCell>
|
| 40 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-12" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 41 |
+
<mxGeometry relative="1" as="geometry">
|
| 42 |
+
<mxPoint x="209.5" y="310" as="sourcePoint" />
|
| 43 |
+
<mxPoint x="209.5" y="260" as="targetPoint" />
|
| 44 |
+
</mxGeometry>
|
| 45 |
+
</mxCell>
|
| 46 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-14" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 47 |
+
<mxGeometry relative="1" as="geometry">
|
| 48 |
+
<mxPoint x="489.5" y="310" as="sourcePoint" />
|
| 49 |
+
<mxPoint x="489.5" y="260" as="targetPoint" />
|
| 50 |
+
</mxGeometry>
|
| 51 |
+
</mxCell>
|
| 52 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-15" value="<font face="Ubuntu" style="font-size: 20px;"><b>x<sub>2</sub></b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 53 |
+
<mxGeometry x="185" y="450" width="50" height="50" as="geometry" />
|
| 54 |
+
</mxCell>
|
| 55 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-17" value="<font face="Ubuntu" style=""><b style=""><span style="font-size: 20px;">x</span><span style="font-size: 16.6667px;"><sub>n</sub></span></b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 56 |
+
<mxGeometry x="465" y="450" width="50" height="50" as="geometry" />
|
| 57 |
+
</mxCell>
|
| 58 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-18" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 59 |
+
<mxGeometry relative="1" as="geometry">
|
| 60 |
+
<mxPoint x="209.5" y="440" as="sourcePoint" />
|
| 61 |
+
<mxPoint x="209.5" y="390" as="targetPoint" />
|
| 62 |
+
</mxGeometry>
|
| 63 |
+
</mxCell>
|
| 64 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-20" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 65 |
+
<mxGeometry relative="1" as="geometry">
|
| 66 |
+
<mxPoint x="489.5" y="440" as="sourcePoint" />
|
| 67 |
+
<mxPoint x="489.5" y="390" as="targetPoint" />
|
| 68 |
+
</mxGeometry>
|
| 69 |
+
</mxCell>
|
| 70 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-21" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#B266FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 71 |
+
<mxGeometry relative="1" as="geometry">
|
| 72 |
+
<mxPoint x="110" y="349.78" as="sourcePoint" />
|
| 73 |
+
<mxPoint x="170.5" y="349.78" as="targetPoint" />
|
| 74 |
+
</mxGeometry>
|
| 75 |
+
</mxCell>
|
| 76 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-22" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#B266FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 77 |
+
<mxGeometry relative="1" as="geometry">
|
| 78 |
+
<mxPoint x="250" y="349.76" as="sourcePoint" />
|
| 79 |
+
<mxPoint x="310.5" y="349.76" as="targetPoint" />
|
| 80 |
+
</mxGeometry>
|
| 81 |
+
</mxCell>
|
| 82 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-23" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#B266FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 83 |
+
<mxGeometry relative="1" as="geometry">
|
| 84 |
+
<mxPoint x="394.75" y="349.76" as="sourcePoint" />
|
| 85 |
+
<mxPoint x="455.25" y="349.76" as="targetPoint" />
|
| 86 |
+
</mxGeometry>
|
| 87 |
+
</mxCell>
|
| 88 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-24" value="<font data-font-src="https://fonts.googleapis.com/css?family=Italianno" face="Italianno" style="font-size: 25px;"><span style="font-size: 25px;">h<sub style="font-size: 25px;">1</sub></span></font>" style="text;html=1;align=center;verticalAlign=middle;whiteSpace=wrap;rounded=0;fontSize=25;fontStyle=1" parent="1" vertex="1">
|
| 89 |
+
<mxGeometry x="110" y="320" width="60" height="30" as="geometry" />
|
| 90 |
+
</mxCell>
|
| 91 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-25" value="<font style="font-size: 25px;"><span style="font-size: 25px;"><span style="font-size: 25px;">h</span><span style="font-size: 25px;"><sub style="font-size: 25px;">2</sub></span></span></font>" style="text;html=1;align=center;verticalAlign=middle;whiteSpace=wrap;rounded=0;fontFamily=Italianno;fontSource=https%3A%2F%2Ffonts.googleapis.com%2Fcss%3Ffamily%3DItalianno;fontSize=25;fontStyle=1" parent="1" vertex="1">
|
| 92 |
+
<mxGeometry x="250" y="320" width="60" height="30" as="geometry" />
|
| 93 |
+
</mxCell>
|
| 94 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-26" value="<font style="font-size: 25px;"><span style="font-size: 25px;"><span style="font-size: 25px;">hn</span></span></font>" style="text;html=1;align=center;verticalAlign=middle;whiteSpace=wrap;rounded=0;fontFamily=Italianno;fontSource=https%3A%2F%2Ffonts.googleapis.com%2Fcss%3Ffamily%3DItalianno;fontSize=25;fontStyle=1" parent="1" vertex="1">
|
| 95 |
+
<mxGeometry x="390" y="320" width="60" height="30" as="geometry" />
|
| 96 |
+
</mxCell>
|
| 97 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-27" value="<font face="Ubuntu" size="1" style="" color="#ffffff"><b style="font-size: 23px;">RNN</b></font>" style="rounded=1;whiteSpace=wrap;html=1;fillColor=#000000;strokeColor=none;fontColor=#FF6666;" parent="1" vertex="1">
|
| 98 |
+
<mxGeometry x="-140" y="320" width="60" height="60" as="geometry" />
|
| 99 |
+
</mxCell>
|
| 100 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-28" value="<font face="Ubuntu" style="font-size: 20px;"><b>seq</b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 101 |
+
<mxGeometry x="-135" y="450" width="50" height="50" as="geometry" />
|
| 102 |
+
</mxCell>
|
| 103 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-29" value="<font size="1" face="Ubuntu"><b style="font-size: 13px;">output</b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" parent="1" vertex="1">
|
| 104 |
+
<mxGeometry x="-135" y="200" width="50" height="50" as="geometry" />
|
| 105 |
+
</mxCell>
|
| 106 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-30" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 107 |
+
<mxGeometry relative="1" as="geometry">
|
| 108 |
+
<mxPoint x="-110.25999999999999" y="310" as="sourcePoint" />
|
| 109 |
+
<mxPoint x="-110.25999999999999" y="260" as="targetPoint" />
|
| 110 |
+
</mxGeometry>
|
| 111 |
+
</mxCell>
|
| 112 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-31" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.5;exitY=0;exitDx=0;exitDy=0;strokeWidth=3;strokeColor=#6666FF;fontColor=#FF6666;" parent="1" edge="1">
|
| 113 |
+
<mxGeometry relative="1" as="geometry">
|
| 114 |
+
<mxPoint x="-110.25999999999999" y="440" as="sourcePoint" />
|
| 115 |
+
<mxPoint x="-110.25999999999999" y="390" as="targetPoint" />
|
| 116 |
+
</mxGeometry>
|
| 117 |
+
</mxCell>
|
| 118 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-32" style="edgeStyle=orthogonalEdgeStyle;rounded=0;orthogonalLoop=1;jettySize=auto;html=1;exitX=0.25;exitY=0;exitDx=0;exitDy=0;entryX=0.25;entryY=1;entryDx=0;entryDy=0;strokeWidth=3;curved=1;" parent="1" source="Kn0003oJxsBQeWTrvDDb-27" target="Kn0003oJxsBQeWTrvDDb-27" edge="1">
|
| 119 |
+
<mxGeometry relative="1" as="geometry">
|
| 120 |
+
<Array as="points">
|
| 121 |
+
<mxPoint x="-125" y="290" />
|
| 122 |
+
<mxPoint x="-210" y="290" />
|
| 123 |
+
<mxPoint x="-210" y="410" />
|
| 124 |
+
<mxPoint x="-125" y="410" />
|
| 125 |
+
</Array>
|
| 126 |
+
</mxGeometry>
|
| 127 |
+
</mxCell>
|
| 128 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-33" value="" style="shape=flexArrow;endArrow=classic;html=1;rounded=0;strokeWidth=3;" parent="1" edge="1">
|
| 129 |
+
<mxGeometry width="50" height="50" relative="1" as="geometry">
|
| 130 |
+
<mxPoint x="-70" y="350" as="sourcePoint" />
|
| 131 |
+
<mxPoint x="30" y="350" as="targetPoint" />
|
| 132 |
+
</mxGeometry>
|
| 133 |
+
</mxCell>
|
| 134 |
+
<mxCell id="Kn0003oJxsBQeWTrvDDb-34" value="<b><font style="font-size: 19px;" face="Ubuntu">Unfold</font></b>" style="text;html=1;align=center;verticalAlign=middle;whiteSpace=wrap;rounded=0;" parent="1" vertex="1">
|
| 135 |
+
<mxGeometry x="-50" y="290" width="60" height="30" as="geometry" />
|
| 136 |
+
</mxCell>
|
| 137 |
+
<mxCell id="phTSMtF67GbWN2Al6Nvf-5" value="<b><font style="font-size: 25px;" face="Ubuntu">. . .</font></b>" style="text;html=1;align=center;verticalAlign=middle;whiteSpace=wrap;rounded=0;" vertex="1" parent="1">
|
| 138 |
+
<mxGeometry x="323" y="330" width="60" height="30" as="geometry" />
|
| 139 |
+
</mxCell>
|
| 140 |
+
<mxCell id="phTSMtF67GbWN2Al6Nvf-6" value="<b style="font-family: Ubuntu; font-size: 20px;">o</b><b style="font-family: Ubuntu; font-size: 13.8889px;"><sub>i</sub></b>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#FF3399;fontColor=#FFFFFF;" vertex="1" parent="1">
|
| 141 |
+
<mxGeometry x="323" y="200" width="50" height="50" as="geometry" />
|
| 142 |
+
</mxCell>
|
| 143 |
+
<mxCell id="phTSMtF67GbWN2Al6Nvf-7" value="<font face="Ubuntu" style=""><b style=""><span style="font-size: 20px;">x</span><span style="font-size: 13.8889px;"><sub>i</sub></span></b></font>" style="ellipse;whiteSpace=wrap;html=1;aspect=fixed;fillColor=#00CC00;fontColor=#FFFFFF;" vertex="1" parent="1">
|
| 144 |
+
<mxGeometry x="323" y="450" width="50" height="50" as="geometry" />
|
| 145 |
+
</mxCell>
|
| 146 |
+
</root>
|
| 147 |
+
</mxGraphModel>
|
| 148 |
+
</diagram>
|
| 149 |
+
</mxfile>
|
docs/source/img/rnn.png
ADDED
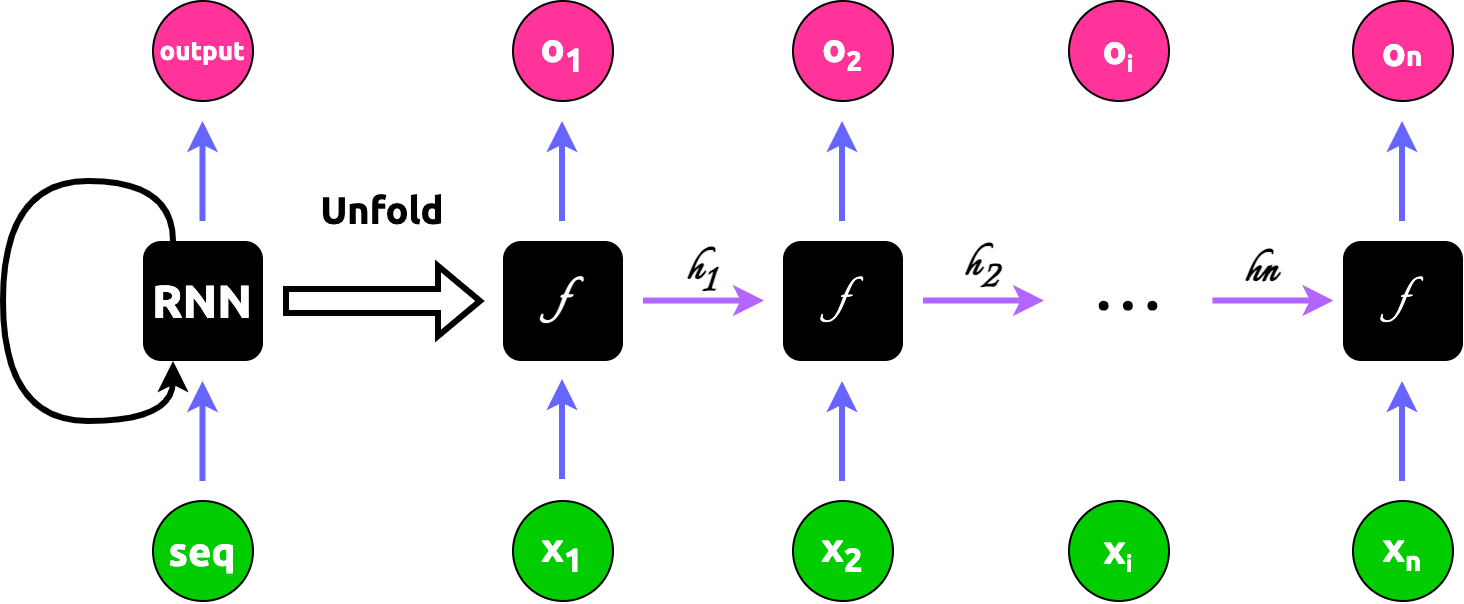
|
docs/source/lamassu.rst
CHANGED
|
@@ -5,5 +5,5 @@ Lamassu
|
|
| 5 |
.. toctree::
|
| 6 |
:maxdepth: 100
|
| 7 |
|
| 8 |
-
rnn/
|
| 9 |
speech/sampling.rst
|
|
|
|
| 5 |
.. toctree::
|
| 6 |
:maxdepth: 100
|
| 7 |
|
| 8 |
+
rnn/rnn
|
| 9 |
speech/sampling.rst
|
docs/source/rnn/rnn.rst
ADDED
|
@@ -0,0 +1,612 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
================================================
|
| 2 |
+
Introduction to Recurrent Neural Networks (RNNs)
|
| 3 |
+
================================================
|
| 4 |
+
|
| 5 |
+
.. admonition:: Prerequisite
|
| 6 |
+
|
| 7 |
+
This article has the following prerequisites:
|
| 8 |
+
|
| 9 |
+
1. *Chapter 4 - Artificial Neural Networks* (p. 81) of `MACHINE LEARNING by Mitchell, Thom M. (1997)`_ Paperback
|
| 10 |
+
2. *Deep Learning (Adaptive Computation and Machine Learning series), Ian Goodfellow*
|
| 11 |
+
|
| 12 |
+
.. contents:: Table of Contents
|
| 13 |
+
:depth: 2
|
| 14 |
+
|
| 15 |
+
We all heard of this buz word "LLM" (Large Language Model). But let's put that aside for just a second and look at a
|
| 16 |
+
much simpler one called "character-level language model" where, for example, we input a prefix of a word such as
|
| 17 |
+
"hell" and the model outputs a complete word "hello". That is, this language model predicts the next character of a
|
| 18 |
+
character sequence
|
| 19 |
+
|
| 20 |
+
This is like a Math function where we have:
|
| 21 |
+
|
| 22 |
+
.. math::
|
| 23 |
+
|
| 24 |
+
f(\text{“hell"}) = \text{“hello"}
|
| 25 |
+
|
| 26 |
+
.. NOTE::
|
| 27 |
+
|
| 28 |
+
We call inputs like "hell" as **sequence**
|
| 29 |
+
|
| 30 |
+
How do we obtain a function like this? One approach is to have 4 black boxes, each of which takes a single character as
|
| 31 |
+
input and calculates an output:
|
| 32 |
+
|
| 33 |
+
.. figure:: ../img/rnn-4-black-boxes.png
|
| 34 |
+
:align: center
|
| 35 |
+
:width: 50%
|
| 36 |
+
|
| 37 |
+
But one might have noticed that if the 3rd function (box) produces :math:`f(‘l') = ‘l'`, then why would the 4th function
|
| 38 |
+
(box), given the same input, gives a different output of 'o'? This suggest that we should take the "**history**" into
|
| 39 |
+
account. Instead of having :math:`f` depend on 1 parameter, we now have it take 2 parameters.
|
| 40 |
+
|
| 41 |
+
1: a character;
|
| 42 |
+
2: a variable that summarizes the previous calculations:
|
| 43 |
+
|
| 44 |
+
.. figure:: ../img/rnn-4-black-boxes-connected.png
|
| 45 |
+
:align: center
|
| 46 |
+
:width: 50%
|
| 47 |
+
|
| 48 |
+
Now it makes much more sense with:
|
| 49 |
+
|
| 50 |
+
.. math::
|
| 51 |
+
|
| 52 |
+
f(\text{‘l'}, h_2) = \text{‘l'}
|
| 53 |
+
|
| 54 |
+
f(\text{‘l'}, h_3) = \text{‘o'}
|
| 55 |
+
|
| 56 |
+
But what if we want to predict a longer or shorter word? For example, how about predicting "cat" by "ca"? That's simple,
|
| 57 |
+
we will have 2 black boxes to do the work.
|
| 58 |
+
|
| 59 |
+
.. figure:: ../img/rnn-multi-sequences.png
|
| 60 |
+
:align: center
|
| 61 |
+
|
| 62 |
+
What if the function :math:`f` is not smart enough to produce the correct output everytime? We will simply collect a lot
|
| 63 |
+
of examples such as "cat" and "hello", and feed them into the boxes to train them until they can output correct
|
| 64 |
+
vocabulary like "cat" and "hello".
|
| 65 |
+
|
| 66 |
+
This is the idea behind RNN
|
| 67 |
+
|
| 68 |
+
- It's recurrent because the boxed function gets invoked repeatedly for each element of the sequence. In the case of our
|
| 69 |
+
character-level language model, element is a character such as "e" and sequence is a string like "hell"
|
| 70 |
+
|
| 71 |
+
.. figure:: ../img/rnn.png
|
| 72 |
+
:align: center
|
| 73 |
+
|
| 74 |
+
Each function :math:`f` is a network unit containing 2 perceptrons. One perceptron computes the "history" like
|
| 75 |
+
:math:`h_1`, :math:`h_2`, :math:`h_3`. Its formula is very similar to that of perceptron:
|
| 76 |
+
|
| 77 |
+
.. math::
|
| 78 |
+
|
| 79 |
+
h^{(t)} = g_1\left( W_{hh}h^{(t - 1)} + W_{xh}x^{(t)} + b_h \right)
|
| 80 |
+
|
| 81 |
+
where :math:`t` is the index of the "black boxes" shown above. In our example of "hell",
|
| 82 |
+
:math:`t \in \{ 1, 2, 3, 4 \}`
|
| 83 |
+
|
| 84 |
+
The other perceptron computes the output like 'e', 'l', 'l', 'o'. We call those value :math:`y` which is computed as
|
| 85 |
+
|
| 86 |
+
.. math::
|
| 87 |
+
|
| 88 |
+
o^{(t)} = g_2\left( W_{yh}h^{(t)} + b_o \right)
|
| 89 |
+
|
| 90 |
+
.. admonition:: What are :math:`g_1` and :math:`g_2`?
|
| 91 |
+
|
| 92 |
+
They are *activation functions* which are used to change the linear function in a perceptron to a non-linear
|
| 93 |
+
function. Please refer to `MACHINE LEARNING by Mitchell, Thom M. (1997)`_ Paperback (page 96) for why we bump it
|
| 94 |
+
to non-linear
|
| 95 |
+
|
| 96 |
+
A typical activation function for :math:`g_1` is :math:`tanh`:
|
| 97 |
+
|
| 98 |
+
.. math::
|
| 99 |
+
|
| 100 |
+
tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}
|
| 101 |
+
|
| 102 |
+
In practice, :math:`g_2` is constance, i.e. :math:`g_2 = 1`
|
| 103 |
+
|
| 104 |
+
|
| 105 |
+
Forward Propagation Equations for RNN
|
| 106 |
+
-------------------------------------
|
| 107 |
+
|
| 108 |
+
We now develop the forward propagation equations for the RNN. We assume the hyperbolic tangent activation function and
|
| 109 |
+
that the output is discrete, as if the RNN is used to predict words or characters. A natural way to represent discrete
|
| 110 |
+
variables is to regard the output :math:`\boldsymbol{o}` as giving the unnormalized log probabilities of each possible value of
|
| 111 |
+
the discrete variable. We can then apply the softmax (we will disucss softmax function in the next section) operation as
|
| 112 |
+
a post-processing step to obtain a vector :math:`\boldsymbol{\hat{y}}` of normalized probabilities over the output. Forward
|
| 113 |
+
propagation begins with a specification of the initial state :math:`\boldsymbol{h}^{(0)}`. Then, for each time step from
|
| 114 |
+
:math:`t = 1` to :math:`t = \tau`, we apply the following update equations:
|
| 115 |
+
|
| 116 |
+
.. math::
|
| 117 |
+
|
| 118 |
+
\color{green} \boxed{
|
| 119 |
+
\begin{gather*}
|
| 120 |
+
\boldsymbol{h}^{(t)} = \tanh\left( \boldsymbol{W_{hh}}h^{(t - 1)} + \boldsymbol{W_{xh}}x^{(t)} + \boldsymbol{b_h} \right) \\ \\
|
| 121 |
+
\boldsymbol{o}^{(t)} = \boldsymbol{W_{yh}}\boldsymbol{h}^{(t)} + \boldsymbol{b_o} \\ \\
|
| 122 |
+
\boldsymbol{\hat{y}} = softmax(\boldsymbol{o}^{(t)})
|
| 123 |
+
\end{gather*}
|
| 124 |
+
}
|
| 125 |
+
|
| 126 |
+
Note that this recurrent network maps an input sequence to an output sequence of the same length.
|
| 127 |
+
|
| 128 |
+
Loss Function of RNN
|
| 129 |
+
--------------------
|
| 130 |
+
|
| 131 |
+
According to the discussion of `MACHINE LEARNING by Mitchell, Thom M. (1997)`_, the key for training RNN or any neural
|
| 132 |
+
network is through "specifying a measure for the training error". We call this measure a *loss function*.
|
| 133 |
+
|
| 134 |
+
In RNN, the total loss for a given sequence of input :math:`\boldsymbol{x}` paired with a sequence of expected
|
| 135 |
+
:math:`\boldsymbol{y}` is the sum of the losses over all the time steps, i.e.
|
| 136 |
+
|
| 137 |
+
.. math::
|
| 138 |
+
|
| 139 |
+
\mathcal{L}\left( \{ \boldsymbol{x}^{(1)}, ..., \boldsymbol{x}^{(\tau)} \}, \{ \boldsymbol{y}^{(1)}, ..., \boldsymbol{y}^{(\tau)} \} \right) = \sum_t^{\tau} \mathcal{L}^{(t)} = \sum_t^{\tau}\log\boldsymbol{\hat{y}}^{(t)}
|
| 140 |
+
|
| 141 |
+
Why would we have :math:`\mathcal{L}^{(t)} = \log\boldsymbol{\hat{y}}^{(t)}`? We need to learn *Softmax Activation* first.
|
| 142 |
+
|
| 143 |
+
.. admonition:: Softmax Function by `Wikipedia <https://en.wikipedia.org/wiki/Softmax_function>`_
|
| 144 |
+
|
| 145 |
+
The softmax function takes as input a vector :math:`z` of :math:`K` real numbers, and normalizes it into a
|
| 146 |
+
probability distribution consisting of :math:`K` probabilities proportional to the exponentials of the input
|
| 147 |
+
numbers. That is, prior to applying softmax, some vector components could be negative, or greater than one; and
|
| 148 |
+
might not sum to 1; but after applying softmax, each component will be in the interval :math:`(0, 1)` and the
|
| 149 |
+
components will add up to 1, so that they can be interpreted as probabilities. Furthermore, the larger input
|
| 150 |
+
components will correspond to larger probabilities.
|
| 151 |
+
|
| 152 |
+
For a vector :math:`z` of :math:`K` real numbers, the the standard (unit) softmax function
|
| 153 |
+
:math:`\sigma: \mathbb{R}^K \mapsto (0, 1)^K`, where :math:`K \ge 1` is defined by
|
| 154 |
+
|
| 155 |
+
.. math::
|
| 156 |
+
|
| 157 |
+
\sigma(\boldsymbol{z})_i = \frac{e^{z_i}}{\sum_{j = 1}^Ke^{z_j}}
|
| 158 |
+
|
| 159 |
+
where :math:`i = 1, 2, ..., K` and :math:`\boldsymbol{x} = (x_1, x_2, ..., x_K) \in \mathbb{R}^K`
|
| 160 |
+
|
| 161 |
+
In the context of RNN,
|
| 162 |
+
|
| 163 |
+
.. math::
|
| 164 |
+
|
| 165 |
+
\sigma(\boldsymbol{o})_i = -\frac{e^{o_i}}{\sum_{j = 1}^ne^{o_j}}
|
| 166 |
+
|
| 167 |
+
where
|
| 168 |
+
|
| 169 |
+
- :math:`n` is the length of a sequence feed into the RNN
|
| 170 |
+
- :math:`o_i` is the output by perceptron unit `i`
|
| 171 |
+
- :math:`i = 1, 2, ..., n`,
|
| 172 |
+
- :math:`\boldsymbol{o} = (o_1, o_2, ..., o_n) \in \mathbb{R}^n`
|
| 173 |
+
|
| 174 |
+
The softmax function takes an N-dimensional vector of arbitrary real values and produces another N-dimensional vector
|
| 175 |
+
with real values in the range (0, 1) that add up to 1.0. It maps :math:`\mathbb{R}^N \rightarrow \mathbb{R}^N`
|
| 176 |
+
|
| 177 |
+
.. math::
|
| 178 |
+
|
| 179 |
+
\sigma(\boldsymbol{o}): \begin{pmatrix}o_1\\o_2\\\dots\\o_n\end{pmatrix} \rightarrow \begin{pmatrix}\sigma_1\\\sigma_2\\\dots\\\sigma_n\end{pmatrix}
|
| 180 |
+
|
| 181 |
+
This property of softmax function that it outputs a probability distribution makes it suitable for probabilistic
|
| 182 |
+
interpretation in classification tasks. Neural networks, however, are commonly trained under a log loss (or
|
| 183 |
+
cross-entropy) regime
|
| 184 |
+
|
| 185 |
+
We are going to compute the derivative of the softmax function because we will be using it for training our RNN model
|
| 186 |
+
shortly. But before diving in, it is important to keep in mind that Softmax is fundamentally a vector function. It takes
|
| 187 |
+
a vector as input and produces a vector as output; in other words, it has multiple inputs and multiple outputs.
|
| 188 |
+
Therefore, we cannot just ask for "the derivative of softmax"; We should instead specify:
|
| 189 |
+
|
| 190 |
+
1. Which component (output element) of softmax we're seeking to find the derivative of.
|
| 191 |
+
2. Since softmax has multiple inputs, with respect to which input element the partial derivative is computed.
|
| 192 |
+
|
| 193 |
+
What we're looking for is the partial derivatives of
|
| 194 |
+
|
| 195 |
+
.. math::
|
| 196 |
+
|
| 197 |
+
\frac{\partial \sigma_i}{\partial o_k} = \frac{\partial }{\partial o_k} \frac{e^{o_i}}{\sum_{j = 1}^ne^{o_j}}
|
| 198 |
+
|
| 199 |
+
|
| 200 |
+
:math:`\frac{\partial \sigma_i}{\partial o_k}` **is the partial derivative of the i-th output with respect with the
|
| 201 |
+
k-th input**.
|
| 202 |
+
|
| 203 |
+
We'll be using the quotient rule of derivatives. For :math:`h(x) = \frac{f(x)}{g(x)}` where both :math:`f` and :math:`g`
|
| 204 |
+
are differentiable and :math:`g(x) \ne 0`, The `quotient rule <https://en.wikipedia.org/wiki/Quotient_rule>`_ states
|
| 205 |
+
that the derivative of :math:`h(x)` is
|
| 206 |
+
|
| 207 |
+
.. math::
|
| 208 |
+
|
| 209 |
+
h'(x) = \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)}
|
| 210 |
+
|
| 211 |
+
In our case, we have
|
| 212 |
+
|
| 213 |
+
.. math::
|
| 214 |
+
|
| 215 |
+
f'(o_k) = \frac{\partial}{\partial o_k} e^{o_i} = \begin{cases}
|
| 216 |
+
e^{o_k}, & \text{if}\ i = k \\
|
| 217 |
+
0, & \text{otherwise}
|
| 218 |
+
\end{cases}
|
| 219 |
+
|
| 220 |
+
.. math::
|
| 221 |
+
|
| 222 |
+
g'(o_k) = \frac{\partial}{\partial o_k} \sum_{j = 1}^ne^{o_j} = \left( \frac{\partial e^{o_1}}{\partial o_k} + \frac{\partial e^{o_2}}{\partial o_k} + \dots + \frac{\partial e^{o_k}}{\partial o_k} + \dots + \frac{\partial e^{o_n}}{\partial o_k} \right) = \frac{\partial e^{o_k}}{\partial o_k} = e^{o_k}
|
| 223 |
+
|
| 224 |
+
The rest of it becomes trivial then. When :math:`i = k`,
|
| 225 |
+
|
| 226 |
+
.. math::
|
| 227 |
+
|
| 228 |
+
\frac{\partial \sigma_i}{\partial o_k} = \frac{e^{o_k} \sum_{j = 1}^ne^{o_j} - e^{o_k} e^{o_i}}{\left( \sum_{j = 1}^ne^{o_j} \right)^2}
|
| 229 |
+
= \frac{e^{o_i} \sum_{j = 1}^ne^{o_j} - e^{o_i} e^{o_i}}{\left( \sum_{j = 1}^ne^{o_j} \right)^2}
|
| 230 |
+
= \frac{e^{o_i}}{\sum_{j = 1}^ne^{o_j}} \frac{\sum_{j = 1}^ne^{o_j} - e^{o_i}}{\sum_{j = 1}^ne^{o_j}} \\
|
| 231 |
+
|
| 232 |
+
= \sigma_i\left( \frac{\sum_{j = 1}^ne^{o_j}}{\sum_{j = 1}^ne^{o_j}} - \frac{e^{o_i}}{\sum_{j = 1}^ne^{o_j}} \right)
|
| 233 |
+
= \sigma_i \left( 1 - \sigma_i \right)
|
| 234 |
+
|
| 235 |
+
When :math:`i \ne k`
|
| 236 |
+
|
| 237 |
+
.. math::
|
| 238 |
+
|
| 239 |
+
\frac{\partial \sigma_i}{\partial o_k} = \frac{-e^{o_k} e^{o_i}}{\left( \sum_{j = 1}^ne^{o_j} \right)^2} = -\sigma_i\sigma_k
|
| 240 |
+
|
| 241 |
+
This concludes the derivative of the softmax function:
|
| 242 |
+
|
| 243 |
+
.. math::
|
| 244 |
+
|
| 245 |
+
\frac{\partial \sigma_i}{\partial o_k} = \begin{cases}
|
| 246 |
+
\sigma_i \left( 1 - \sigma_i \right), & \text{if}\ i = k \\
|
| 247 |
+
-\sigma_i\sigma_k, & \text{otherwise}
|
| 248 |
+
\end{cases}
|
| 249 |
+
|
| 250 |
+
Cross-Entropy
|
| 251 |
+
"""""""""""""
|
| 252 |
+
|
| 253 |
+
.. admonition:: Cross-Entropy `Wikipedia <https://en.wikipedia.org/wiki/Cross-entropy>`_
|
| 254 |
+
|
| 255 |
+
In information theory, the cross-entropy between two probability distributions :math:`p` and :math:`q` over the same
|
| 256 |
+
underlying set of events measures the average number of bits needed to identify an event drawn from the set if a
|
| 257 |
+
coding scheme used for the set is optimized for an estimated probability distribution :math:`q`, rather than the
|
| 258 |
+
true distribution :math:`p`
|
| 259 |
+
|
| 260 |
+
Confused? Let's put it in the context of Machine Learning.
|
| 261 |
+
|
| 262 |
+
Machine Learning sees the world based on probability. The "probability distribution" identifies the various tasks to
|
| 263 |
+
learn. For example, a daily language such as English or Chinese, can be seen as a probability distribution. The
|
| 264 |
+
probability of "name" followed by "is" is far greater than "are" as in "My name is Jack". We call such language
|
| 265 |
+
distribution :math:`p`. The task of RNN (or Machine Learning in general) is to learn an approximated distribution of
|
| 266 |
+
:math:`p`; we call this approximation :math:`q`
|
| 267 |
+
|
| 268 |
+
"The average number of bits needed" is can be seen as the distance between :math:`p` and :math:`q` given an event. In
|
| 269 |
+
analogy of language, this can be the *quantitative* measure of the deviation between a real language phrase
|
| 270 |
+
"My name is Jack" and "My name are Jack".
|
| 271 |
+
|
| 272 |
+
At this point, it is easy to image that, in the Machine Learning world, the cross entropy indicates the distance between
|
| 273 |
+
what the model believes the output distribution should be and what the original distribution really is.
|
| 274 |
+
|
| 275 |
+
Now we have an intuitive understanding of cross entropy, let's formally define it.
|
| 276 |
+
|
| 277 |
+
The cross-entropy of the discrete probability distribution :math:`q` relative to a distribution :math:`p` over a given
|
| 278 |
+
set is defined as
|
| 279 |
+
|
| 280 |
+
.. math::
|
| 281 |
+
|
| 282 |
+
H(p, q) = -\sum_x p(x)\log q(x)
|
| 283 |
+
|
| 284 |
+
In RNN, the probability distribution of :math:`q(x)` is exactly the softmax function we defined earlier:
|
| 285 |
+
|
| 286 |
+
.. math::
|
| 287 |
+
|
| 288 |
+
\mathcal{L} = -\sum_i p(i)\log\sigma(\boldsymbol{o})_i = -\sum_i \log\sigma(\boldsymbol{o})_i = -\log\boldsymbol{\hat{y}}^{(t)}
|
| 289 |
+
|
| 290 |
+
where
|
| 291 |
+
|
| 292 |
+
- :math:`\boldsymbol{o}` is the predicted sequence by RNN and :math:`o_i` is the i-th element of the predicted sequence
|
| 293 |
+
|
| 294 |
+
.. admonition:: What is the Mathematical form of :math:`p(i)` in RNN? Why would it become 1?
|
| 295 |
+
|
| 296 |
+
By definition, :math:`p(i)` is the *true* distribution whose exact functional form is unknown. In the language of
|
| 297 |
+
Approximation Theory, :math:`p(i)` is the function that RNN is trying to learn or approximate mathematically.
|
| 298 |
+
|
| 299 |
+
Although the :math:`p(i)` makes the exact form of :math:`\mathcal{L}` unknown, computationally :math:`p(i)` is
|
| 300 |
+
perfectly defined in each training example. Taking our "hello" example:
|
| 301 |
+
|
| 302 |
+
.. figure:: ../img/char-level-language-model.png
|
| 303 |
+
:align: center
|
| 304 |
+
:width: 60%
|
| 305 |
+
|
| 306 |
+
The 4 probability distributions of :math:`q(x)` is "reflected" in the **output layer** of this example. They are
|
| 307 |
+
"reflecting" the probability distribution of :math:`q(x)` because they are only :math:`o` values and have not been
|
| 308 |
+
transformed to the :math:`\sigma` distribution yet. But in this case, we are 100% sure that the true probability
|
| 309 |
+
distribution :math:`p(i)` for the 4 outputs are
|
| 310 |
+
|
| 311 |
+
.. math::
|
| 312 |
+
|
| 313 |
+
\begin{pmatrix}0\\1\\0\\0\end{pmatrix}, \begin{pmatrix}0\\0\\1\\0\end{pmatrix}, \begin{pmatrix}0\\0\\1\\0\end{pmatrix}, \begin{pmatrix}0\\0\\0\\1\end{pmatrix}
|
| 314 |
+
|
| 315 |
+
respectively. *That is all we need for calculating the* :math:`\mathcal{L}`
|
| 316 |
+
|
| 317 |
+
Deriving Gradient Descent Weight Update Rule
|
| 318 |
+
--------------------------------------------
|
| 319 |
+
|
| 320 |
+
*Training a RNN model of is the same thing as searching for the optimal values for the following parameters of these two
|
| 321 |
+
perceptrons*:
|
| 322 |
+
|
| 323 |
+
1. :math:`W_{xh}`
|
| 324 |
+
2. :math:`W_{hh}`
|
| 325 |
+
3. :math:`W_{yh}`
|
| 326 |
+
4. :math:`b_h`
|
| 327 |
+
5. :math:`b_o`
|
| 328 |
+
|
| 329 |
+
By the Gradient Descent discussed in `MACHINE LEARNING by Mitchell, Thom M. (1997)`_ tells us we should derive the
|
| 330 |
+
weight updat rule by *taking partial derivatives with respect to all of the variables above*. Let's start with
|
| 331 |
+
:math:`W_{yh}`
|
| 332 |
+
|
| 333 |
+
`MACHINE LEARNING by Mitchell, Thom M. (1997)`_ has mentioned gradients and partial derivatives as being important for
|
| 334 |
+
an optimization algorithm to update, say, the model weights of a neural network to reach an optimal set of weights. The
|
| 335 |
+
use of partial derivatives permits each weight to be updated independently of the others, by calculating the gradient of
|
| 336 |
+
the error curve with respect to each weight in turn.
|
| 337 |
+
|
| 338 |
+
Many of the functions that we usually work with in machine learning are *multivariate*, *vector-valued* functions, which
|
| 339 |
+
means that they map multiple real inputs :math:`n` to multiple real outputs :math:`m`:
|
| 340 |
+
|
| 341 |
+
.. math::
|
| 342 |
+
|
| 343 |
+
f: \mathbb{R}^n \rightarrow \mathbb{R}^m
|
| 344 |
+
|
| 345 |
+
In training a neural network, the backpropagation algorithm is responsible for sharing back the error calculated at the
|
| 346 |
+
output layer among the neurons comprising the different hidden layers of the neural network, until it reaches the input.
|
| 347 |
+
|
| 348 |
+
If our RNN contains only 1 perceptron unit, the error is propagated back by, using the
|
| 349 |
+
`Chain Rule <https://en.wikipedia.org/wiki/Chain_rule>`_ of :math:`\frac{dz}{dx} = \frac{dz}{dy}\frac{dy}{dx}`:
|
| 350 |
+
|
| 351 |
+
.. math::
|
| 352 |
+
|
| 353 |
+
\frac{\partial \mathcal{L}}{\partial W} = \frac{\partial \mathcal{L}}{\partial o}\frac{\partial o}{\partial W}
|
| 354 |
+
|
| 355 |
+
Note that in the RNN mode, :math:`\mathcal{L}` is not a direct function of :math:`W`. Thus its first order derivative
|
| 356 |
+
cannot be computed unless we connect the :math:`\mathcal{L}` to :math:`o` first and then to :math:`W`, because both the
|
| 357 |
+
first order derivatives of :math:`\frac{\partial \mathcal{L}}{\partial o}` and :math:`\frac{\partial o}{\partial W}` are
|
| 358 |
+
defined by the model
|
| 359 |
+
|
| 360 |
+
It is more often the case that we'd have many connected perceptrons populating the network, each attributed a different
|
| 361 |
+
weight. Since this is the case for RNN, we can generalise multiple inputs and multiple outputs using the **Generalized
|
| 362 |
+
Chain Rule**:
|
| 363 |
+
|
| 364 |
+
Consider the case where :math:`x \in \mathbb{R}^m` and :math:`u \in \mathbb{R}^n`; an inner function, :math:`f`, maps
|
| 365 |
+
:math:`m` inputs to :math:`n` outputs, while an outer function, :math:`g`, receives :math:`n` inputs to produce an
|
| 366 |
+
output, :math:`h \in \mathbb{R}^k`. For :math:`i = 1, \dots, m` the generalized chain rule states:
|
| 367 |
+
|
| 368 |
+
.. math::
|
| 369 |
+
|
| 370 |
+
\frac{\partial h}{\partial x_i} = \frac{\partial h}{\partial u_1} \frac{\partial u_1}{\partial x_i} + \frac{\partial h}{\partial u_2} \frac{\partial u_2}{\partial x_i} + \dots + \frac{\partial h}{\partial u_n} \frac{\partial u_n}{\partial x_i} = \sum_{j = 1}^n \frac{\partial h}{\partial u_j} \frac{\partial u_j}{\partial x_i}
|
| 371 |
+
|
| 372 |
+
Therefore, the error propagation of Gradient Descent in RNN is
|
| 373 |
+
|
| 374 |
+
.. math::
|
| 375 |
+
|
| 376 |
+
\color{green} \boxed{
|
| 377 |
+
\begin{align}
|
| 378 |
+
\frac{\partial \mathcal{L}}{\partial W_{yh}} = \sum_{t = 1}^\tau \sum_{i = 1}^n \frac{\partial \mathcal{L}}{\partial o_i^{(t)}} \frac{\partial o_i^{(t)}}{\partial W_{yh}} \\ \\
|
| 379 |
+
\frac{\partial \mathcal{L}}{\partial W_{hh}} = \sum_{t = 1}^\tau \sum_{i = 1}^n \frac{\partial \mathcal{L}}{\partial h_i^{(t)}} \frac{\partial h_i^{(t)}}{\partial W_{hh}} \\ \\
|
| 380 |
+
\frac{\partial \mathcal{L}}{\partial W_{xh}} = \sum_{t = 1}^\tau \sum_{i = 1}^n \frac{\partial \mathcal{L}}{\partial h_i^{(t)}} \frac{\partial h_i^{(t)}}{\partial W_{xh}}
|
| 381 |
+
\end{align}
|
| 382 |
+
}
|
| 383 |
+
|
| 384 |
+
where :math:`n` is the length of a RNN sequence and :math:`t` is the index of timestep
|
| 385 |
+
|
| 386 |
+
.. admonition:: :math:`\sum_{t = 1}^\tau`
|
| 387 |
+
|
| 388 |
+
We assume the error is the sum of all errors of each timestep, which is why we include the :math:`\sum_{t = 1}^\tau`
|
| 389 |
+
term
|
| 390 |
+
|
| 391 |
+
Let's look at :math:`\frac{\partial \mathcal{L}}{W_{yh}}` first
|
| 392 |
+
|
| 393 |
+
.. math::
|
| 394 |
+
|
| 395 |
+
\frac{\partial \mathcal{L}}{W_{yh}} = \sum_{t = 1}^\tau \sum_{i = 1}^n \frac{\partial \mathcal{L}}{\partial o_i^{(t)}} \frac{\partial o_i^{(t)}}{\partial W_{yh}}
|
| 396 |
+
|
| 397 |
+
Since :math:`o_i = \left( W_{yh}h_i + b_o \right)`,
|
| 398 |
+
|
| 399 |
+
.. math::
|
| 400 |
+
|
| 401 |
+
\frac{\partial o_i}{W_{yh}} = \frac{\partial }{W_{yh}}\left( W_{yh}h_i + b_o \right) = h_i
|
| 402 |
+
|
| 403 |
+
For the :math:`\frac{\partial \mathcal{L}}{\partial o_i}` we shall recall from the earlier discussion on softmax
|
| 404 |
+
derivative that we cannot simply have
|
| 405 |
+
|
| 406 |
+
.. math::
|
| 407 |
+
|
| 408 |
+
\frac{\partial \mathcal{L}}{\partial o_i} = -\frac{\partial}{\partial o_i}\sum_i^np(i)\log\sigma_i
|
| 409 |
+
|
| 410 |
+
because we need to
|
| 411 |
+
|
| 412 |
+
1. specify which component (output element) we're seeking to find the derivative of
|
| 413 |
+
2. with respect to which input element the partial derivative is computed
|
| 414 |
+
|
| 415 |
+
Therefore:
|
| 416 |
+
|
| 417 |
+
.. math::
|
| 418 |
+
|
| 419 |
+
\frac{\partial \mathcal{L}}{\partial o_i} = -\frac{\partial}{\partial o_i}\sum_j^np(j)\log\sigma_j = -\sum_j^n\frac{\partial}{\partial o_i}p(j)\log\sigma_j = -\sum_j^np(j)\frac{\partial \log\sigma_j}{\partial o_i}
|
| 420 |
+
|
| 421 |
+
where :math:`n` is the number of timesteps (or the length of a sequence such as "hell")
|
| 422 |
+
|
| 423 |
+
Applying the chain rule again:
|
| 424 |
+
|
| 425 |
+
.. math::
|
| 426 |
+
|
| 427 |
+
-\sum_j^np(j)\frac{\partial \log\sigma_j}{\partial o_i} = -\sum_j^np(j)\frac{1}{\sigma_j}\frac{\partial\sigma_j}{\partial o_i}
|
| 428 |
+
|
| 429 |
+
Recall we have already derived that
|
| 430 |
+
|
| 431 |
+
.. math::
|
| 432 |
+
|
| 433 |
+
\frac{\partial \sigma_i}{\partial o_j} = \begin{cases}
|
| 434 |
+
\sigma_i \left( 1 - \sigma_i \right), & \text{if}\ i = j \\
|
| 435 |
+
-\sigma_i\sigma_j, & \text{otherwise}
|
| 436 |
+
\end{cases}
|
| 437 |
+
|
| 438 |
+
.. math::
|
| 439 |
+
|
| 440 |
+
-\sum_j^np(j)\frac{1}{\sigma_j}\frac{\partial\sigma_j}{\partial o_i} = -\sum_{i = j}^np(j)\frac{1}{\sigma_j}\frac{\partial\sigma_j}{\partial o_i} -\sum_{i \ne j}^np(j)\frac{1}{\sigma_j}\frac{\partial\sigma_j}{\partial o_i} = -p(i)(1 - \sigma_i) + \sum_{i \ne j}^np(j)\sigma_i
|
| 441 |
+
|
| 442 |
+
Observing that
|
| 443 |
+
|
| 444 |
+
.. math::
|
| 445 |
+
|
| 446 |
+
\sum_{j}^np(j) = 1
|
| 447 |
+
|
| 448 |
+
.. math::
|
| 449 |
+
|
| 450 |
+
-p(i)(1 - \sigma_i) + \sum_{i \ne j}^np(j)\sigma_i = -p(i) + p(i)\sigma_i + \sum_{i \ne j}^np(j)\sigma_i = \sigma_i - p(i)
|
| 451 |
+
|
| 452 |
+
.. math::
|
| 453 |
+
|
| 454 |
+
\color{green} \boxed{\frac{\partial \mathcal{L}}{\partial o_i} = \sigma_i - p(i)}
|
| 455 |
+
|
| 456 |
+
.. math::
|
| 457 |
+
|
| 458 |
+
\color{green} \boxed{ \frac{\partial \mathcal{L}}{\partial W_{yh}} = \sum_{t = 1}^\tau \sum_i^n\left[ \sigma_i - p(i) \right] h_i = \sum_{t = 1}^\tau \left( \boldsymbol{\sigma} - \boldsymbol{p} \right) \boldsymbol{h}^{(t)} }
|
| 459 |
+
|
| 460 |
+
.. math::
|
| 461 |
+
|
| 462 |
+
\frac{\partial \mathcal{L}}{b_o} = \sum_{t = 1}^\tau \sum_i^n\frac{\partial \mathcal{L}}{\partial o_i^{(t)}}\frac{\partial o_i^{(t)}}{\partial b_o^{(t)}} = \sum_{t = 1}^\tau \sum_i^n\left[ \sigma_i - p(i) \right] \times 1
|
| 463 |
+
|
| 464 |
+
.. math::
|
| 465 |
+
|
| 466 |
+
\color{green} \boxed{ \frac{\partial \mathcal{L}}{\partial b_o} = \sum_{t = 1}^\tau \sum_i^n\left[ \sigma_i - p(i) \right] = \sum_{t = 1}^\tau \boldsymbol{\sigma} - \boldsymbol{p} }
|
| 467 |
+
|
| 468 |
+
We have at this point derived backpropagating rule for :math:`W_{yh}` and :math:`b_o`:
|
| 469 |
+
|
| 470 |
+
1. :math:`W_{xh}`
|
| 471 |
+
2. :math:`W_{hh}`
|
| 472 |
+
3. ✅ :math:`W_{yh}`
|
| 473 |
+
4. :math:`b_h`
|
| 474 |
+
5. ✅ :math:`b_o`
|
| 475 |
+
|
| 476 |
+
Now let's look at :math:`\frac{\partial \mathcal{L}}{\partial W_{hh}}`:
|
| 477 |
+
|
| 478 |
+
Recall from *Deep Learning*, section 6.5.2, p. 207 that the vector notation of
|
| 479 |
+
:math:`\frac{\partial z}{\partial x_i} = \sum_j \frac{\partial z}{\partial y_j}\frac{\partial y_j}{\partial x_i}` is
|
| 480 |
+
|
| 481 |
+
.. math::
|
| 482 |
+
|
| 483 |
+
\nabla_{\boldsymbol{x}}z = \left( \frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}} \right)^\intercal \nabla_{\boldsymbol{y}}z
|
| 484 |
+
|
| 485 |
+
This gives us a start with:
|
| 486 |
+
|
| 487 |
+
.. math::
|
| 488 |
+
|
| 489 |
+
\begin{align}
|
| 490 |
+
\frac{\partial \mathcal{L}}{\partial W_{hh}} &= \sum_{t = 1}^\tau \sum_{i = 1}^n \frac{\partial \mathcal{L}}{\partial h_i^{(t)}} \frac{\partial h_i^{(t)}}{\partial W_{hh}} \\
|
| 491 |
+
& = \sum_{t = 1}^\tau \left( \frac{\partial \mathcal{L}}{\partial \boldsymbol{h}^{(t)}} \right)^\intercal \nabla_{\boldsymbol{W_{hh}}}\boldsymbol{h}^{(t)} \\
|
| 492 |
+
& = \sum_{t = 1}^\tau \left( \frac{\partial \mathcal{L}}{\partial \boldsymbol{h}^{(t)}} \right)^\intercal \left( \frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{W_{hh}}} \right)^\intercal \nabla_{\boldsymbol{h}^{(t)}}\boldsymbol{h}^{(t)} \\
|
| 493 |
+
& = \sum_{t = 1}^\tau \left( \frac{\partial \mathcal{L}}{\partial \boldsymbol{h}^{(t)}} \right)^\intercal \left( \frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{W_{hh}}} \right)^\intercal \\
|
| 494 |
+
& = \sum_{t = 1}^\tau \left( \frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{W_{hh}}} \right)^\intercal \frac{\partial \mathcal{L}}{\partial \boldsymbol{h}^{(t)}} \\
|
| 495 |
+
& = \sum_{t = 1}^\tau \left( \frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{h}^{(t - 1)}} \right)^\intercal \left( \frac{\partial \boldsymbol{h}^{(t - 1)}}{\partial \boldsymbol{W_{hh}}} \right)^\intercal \frac{\partial \mathcal{L}}{\partial \boldsymbol{h}^{(t)}} \\
|
| 496 |
+
& = \sum_{t = 1}^\tau \left( \frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{h}^{(t - 1)}} \right)^\intercal \left( \frac{\partial \boldsymbol{h}^{(t - 1)}}{\partial \boldsymbol{h}^{(t)}}\frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{h}^{(t)}}\frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{W_{hh}}} \right)^\intercal \frac{\partial \mathcal{L}}{\partial \boldsymbol{h}^{(t)}} \\
|
| 497 |
+
& = \sum_{t = 1}^\tau \left( \frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{h}^{(t - 1)}} \right)^\intercal \left( \frac{\partial \boldsymbol{h}^{(t - 1)}}{\partial \boldsymbol{h}^{(t)}}\frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{W_{hh}}}\frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{h}^{(t)}} \right)^\intercal \frac{\partial \mathcal{L}}{\partial \boldsymbol{h}^{(t)}} \\
|
| 498 |
+
& = \sum_{t = 1}^\tau \left( \frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{h}^{(t - 1)}} \right)^\intercal \left( \frac{\partial \boldsymbol{h}^{(t - 1)}}{\partial \boldsymbol{h}^{(t)}} \right)^\intercal \left( \frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{W_{hh}}} \right)^\intercal \left( \frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{h}^{(t)}} \right)^\intercal \frac{\partial \mathcal{L}}{\partial \boldsymbol{h}^{(t)}} \\
|
| 499 |
+
& = \sum_{t = 1}^\tau \left( \frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{W_{hh}}} \right)^\intercal \left( \frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{h}^{(t)}} \right)^\intercal \frac{\partial \mathcal{L}}{\partial \boldsymbol{h}^{(t)}} \\
|
| 500 |
+
& = \sum_{t = 1}^\tau diag\left[ 1 - \left(\boldsymbol{h}^{(t)}\right)^2 \right] \boldsymbol{h}^{(t - 1)} \nabla_{\boldsymbol{h}^{(t)}}\mathcal{L} \\
|
| 501 |
+
& = \sum_{t = 1}^\tau diag\left[ 1 - \left(\boldsymbol{h}^{(t)}\right)^2 \right] \left( \nabla_{\boldsymbol{h}^{(t)}}\mathcal{L} \right) {\boldsymbol{h}^{(t - 1)}}^\intercal
|
| 502 |
+
\end{align}
|
| 503 |
+
|
| 504 |
+
.. math::
|
| 505 |
+
|
| 506 |
+
\color{green} \boxed{ \frac{\partial \mathcal{L}}{\partial W_{hh}} = \sum_{t = 1}^\tau diag\left[ 1 - \left(\boldsymbol{h}^{(t)}\right)^2 \right] \left( \nabla_{\boldsymbol{h}^{(t)}}\mathcal{L} \right) {\boldsymbol{h}^{(t - 1)}}^\intercal }
|
| 507 |
+
|
| 508 |
+
The equation above leaves us with a term :math:`\nabla_{\boldsymbol{h}^{(t)}}\mathcal{L}`, which we calculate next. Note
|
| 509 |
+
that the back propagation on :math:`\boldsymbol{h}^{(t)}` has source from both :math:`\boldsymbol{o}^{(t)}` and
|
| 510 |
+
:math:`\boldsymbol{h}^{(t + 1)}`. It's gradient, therefore, is given by
|
| 511 |
+
|
| 512 |
+
.. math::
|
| 513 |
+
|
| 514 |
+
\begin{align}
|
| 515 |
+
\nabla_{\boldsymbol{h}^{(t)}}\mathcal{L} &= \left( \frac{\partial \boldsymbol{o}^{(t)}}{\partial \boldsymbol{h}^{(t)}} \right)^\intercal \nabla_{\boldsymbol{o}^{(t)}}\mathcal{L} + \left( \frac{\partial \boldsymbol{h}^{(t + 1)}}{\partial \boldsymbol{h}^{(t)}} \right)^\intercal \nabla_{\boldsymbol{h}^{(t + 1)}}\mathcal{L} \\
|
| 516 |
+
&= \left( \boldsymbol{W_{yh}} \right)^\intercal \nabla_{\boldsymbol{o}^{(t)}}\mathcal{L} + \left( diag\left[ 1 - (\boldsymbol{h}^{(t + 1)})^2 \right] \boldsymbol{W_{hh}} \right)^\intercal \nabla_{\boldsymbol{h}^{(t + 1)}}\mathcal{L} \\
|
| 517 |
+
&= \left( \boldsymbol{W_{yh}} \right)^\intercal \nabla_{\boldsymbol{o}^{(t)}}\mathcal{L}+ \boldsymbol{W_{hh}}^\intercal \nabla_{\boldsymbol{h}^{(t + 1)}}\mathcal{L} \left( diag\left[ 1 - (\boldsymbol{h}^{(t + 1)})^2 \right] \right)
|
| 518 |
+
\end{align}
|
| 519 |
+
|
| 520 |
+
.. math::
|
| 521 |
+
|
| 522 |
+
\color{green} \boxed{ \nabla_{\boldsymbol{h}^{(t)}}\mathcal{L} = \left( \boldsymbol{W_{yh}} \right)^\intercal \nabla_{\boldsymbol{o}^{(t)}}\mathcal{L} + \boldsymbol{W_{hh}}^\intercal \nabla_{\boldsymbol{h}^{(t + 1)}}\mathcal{L} \left( diag\left[ 1 - (\boldsymbol{h}^{(t + 1)})^2 \right] \right) }
|
| 523 |
+
|
| 524 |
+
Note that the 2nd term
|
| 525 |
+
:math:`\boldsymbol{W_{xh}}^\intercal \nabla_{\boldsymbol{h}^{(t + 1)}}\mathcal{L} \left( diag\left[ 1 - (\boldsymbol{h}^{(t + 1)})^2 \right] \right)`
|
| 526 |
+
is zero at first iteration propagating back because for the last-layer (unrolled) of RNN , there's no gradient update
|
| 527 |
+
flow from the next hidden state.
|
| 528 |
+
|
| 529 |
+
So far we have derived backpropagating rule for :math:`W_{hh}`
|
| 530 |
+
|
| 531 |
+
1. :math:`W_{xh}`
|
| 532 |
+
2. ✅ :math:`W_{hh}`
|
| 533 |
+
3. ✅ :math:`W_{yh}`
|
| 534 |
+
4. :math:`b_h`
|
| 535 |
+
5. ✅ :math:`b_o`
|
| 536 |
+
|
| 537 |
+
Let's tackle the remaining :math:`\frac{\partial \mathcal{L}}{\partial W_{xh}}` and :math:`b_h`:
|
| 538 |
+
|
| 539 |
+
.. math::
|
| 540 |
+
|
| 541 |
+
\begin{align}
|
| 542 |
+
\frac{\partial \mathcal{L}}{\partial W_{xh}} &= \sum_{t = 1}^\tau \sum_{i = 1}^n \frac{\partial \mathcal{L}}{\partial h_i^{(t)}} \frac{\partial h_i^{(t)}}{\partial W_{xh}} \\
|
| 543 |
+
&= \sum_{t = 1}^\tau \left( \frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{W_{xh}}} \right)^\intercal \nabla_{\boldsymbol{h}^{(t)}}\mathcal{L} \\
|
| 544 |
+
&= \sum_{t = 1}^\tau \left( diag\left[ 1 - (\boldsymbol{h}^{(t)})^2 \right] \boldsymbol{x}^{(t)} \right)^\intercal \nabla_{\boldsymbol{h}^{(t)}}\mathcal{L} \\
|
| 545 |
+
&= \sum_{t = 1}^\tau \left( diag\left[ 1 - (\boldsymbol{h}^{(t)})^2 \right] \right)^\intercal \nabla_{\boldsymbol{h}^{(t)}}\mathcal{L} \left( \boldsymbol{x}^{(t)} \right)
|
| 546 |
+
\end{align}
|
| 547 |
+
|
| 548 |
+
.. math::
|
| 549 |
+
|
| 550 |
+
\color{green} \boxed{ \frac{\partial \mathcal{L}}{\partial W_{xh}} = \sum_{t = 1}^\tau \left( diag\left[ 1 - (\boldsymbol{h}^{(t)})^2 \right] \right)^\intercal \nabla_{\boldsymbol{h}^{(t)}}\mathcal{L} \left( \boldsymbol{x}^{(t)} \right) }
|
| 551 |
+
|
| 552 |
+
.. math::
|
| 553 |
+
|
| 554 |
+
\begin{align}
|
| 555 |
+
\frac{\partial \mathcal{L}}{\partial b_h} &= \sum_{t = 1}^\tau \sum_{i = 1}^n \frac{\partial \mathcal{L}}{\partial h_i^{(t)}} \frac{\partial h_i^{(t)}}{\partial b_h^{(t)}} \\
|
| 556 |
+
&= \sum_{t = 1}^\tau \left( \frac{\partial h_i^{(t)}}{\partial b_h^{(t)}} \right)^\intercal \nabla_{\boldsymbol{h}^{(t)}}\mathcal{L} \\
|
| 557 |
+
&= \sum_{t = 1}^\tau \left( diag\left[ 1 - (\boldsymbol{h}^{(t)})^2 \right] \right)^\intercal \nabla_{\boldsymbol{h}^{(t)}}\mathcal{L}
|
| 558 |
+
\end{align}
|
| 559 |
+
|
| 560 |
+
.. math::
|
| 561 |
+
|
| 562 |
+
\color{green} \boxed{ \frac{\partial \mathcal{L}}{\partial b_h} = \sum_{t = 1}^\tau \left( diag\left[ 1 - (\boldsymbol{h}^{(t)})^2 \right] \right)^\intercal \nabla_{\boldsymbol{h}^{(t)}}\mathcal{L} }
|
| 563 |
+
|
| 564 |
+
This concludes our propagation rules for training RNN:
|
| 565 |
+
|
| 566 |
+
.. math::
|
| 567 |
+
|
| 568 |
+
\color{green} \boxed{
|
| 569 |
+
\begin{gather*}
|
| 570 |
+
\frac{\partial \mathcal{L}}{\partial W_{xh}} = \sum_{t = 1}^\tau \left( diag\left[ 1 - (\boldsymbol{h}^{(t)})^2 \right] \right)^\intercal \nabla_{\boldsymbol{h}^{(t)}}\mathcal{L} \left( \boldsymbol{x}^{(t)} \right) \\ \\
|
| 571 |
+
\frac{\partial \mathcal{L}}{\partial W_{hh}} = \sum_{t = 1}^\tau diag\left[ 1 - \left(\boldsymbol{h}^{(t)}\right)^2 \right] \left( \nabla_{\boldsymbol{h}^{(t)}}\mathcal{L} \right) {\boldsymbol{h}^{(t - 1)}}^\intercal \\ \\
|
| 572 |
+
\frac{\partial \mathcal{L}}{\partial W_{yh}} = \sum_{t = 1}^\tau \left( \boldsymbol{\sigma} - \boldsymbol{p} \right) \boldsymbol{h}^{(t)} \\ \\
|
| 573 |
+
\frac{\partial \mathcal{L}}{\partial b_h} = \sum_{t = 1}^\tau \left( diag\left[ 1 - (\boldsymbol{h}^{(t)})^2 \right] \right)^\intercal \nabla_{\boldsymbol{h}^{(t)}}\mathcal{L} \\ \\
|
| 574 |
+
\frac{\partial \mathcal{L}}{\partial b_o} =\sum_{t = 1}^\tau \boldsymbol{\sigma} - \boldsymbol{p}
|
| 575 |
+
\end{gather*}
|
| 576 |
+
}
|
| 577 |
+
|
| 578 |
+
where
|
| 579 |
+
|
| 580 |
+
.. math::
|
| 581 |
+
|
| 582 |
+
\color{green} \boxed{ \nabla_{\boldsymbol{h}^{(t)}}\mathcal{L} = \left( \boldsymbol{W_{yh}} \right)^\intercal \nabla_{\boldsymbol{o}^{(t)}}\mathcal{L}+ \boldsymbol{W_{hh}}^\intercal \nabla_{\boldsymbol{h}^{(t + 1)}}\mathcal{L} \left( diag\left[ 1 - (\boldsymbol{h}^{(t + 1)})^2 \right] \right) }
|
| 583 |
+
|
| 584 |
+
Computational Gradient Descent Weight Update Rule
|
| 585 |
+
-------------------------------------------------
|
| 586 |
+
|
| 587 |
+
What does the propagation rules above look like in Python?
|
| 588 |
+
|
| 589 |
+
Example
|
| 590 |
+
-------
|
| 591 |
+
|
| 592 |
+
`Pride and Prejudice by Jane Austen <https://www.gutenberg.org/ebooks/1342>`_
|
| 593 |
+
|
| 594 |
+
|
| 595 |
+
.. code-block:: python
|
| 596 |
+
|
| 597 |
+
|
| 598 |
+
|
| 599 |
+
|
| 600 |
+
|
| 601 |
+
|
| 602 |
+
|
| 603 |
+
|
| 604 |
+
|
| 605 |
+
.. _`exploding gradient`: https://qubitpi.github.io/stanford-cs231n.github.io/rnn/#vanilla-rnn-gradient-flow--vanishing-gradient-problem
|
| 606 |
+
|
| 607 |
+
.. _`MACHINE LEARNING by Mitchell, Thom M. (1997)`: https://a.co/d/bjmsEOg
|
| 608 |
+
|
| 609 |
+
.. _`loss function`: https://qubitpi.github.io/stanford-cs231n.github.io/neural-networks-2/#losses
|
| 610 |
+
.. _`LSTM Formulation`: https://qubitpi.github.io/stanford-cs231n.github.io/rnn/#lstm-formulation
|
| 611 |
+
|
| 612 |
+
.. _`Vanilla RNN Gradient Flow & Vanishing Gradient Problem`: https://qubitpi.github.io/stanford-cs231n.github.io/rnn/#vanilla-rnn-gradient-flow--vanishing-gradient-problem
|
docs/source/rnn/vanilla.rst
DELETED
|
@@ -1,176 +0,0 @@
|
|
| 1 |
-
================================================
|
| 2 |
-
Introduction to Recurrent Neural Networks (RNNs)
|
| 3 |
-
================================================
|
| 4 |
-
|
| 5 |
-
.. contents:: Table of Contents
|
| 6 |
-
:depth: 2
|
| 7 |
-
|
| 8 |
-
|
| 9 |
-
Mathematical Formulation
|
| 10 |
-
------------------------
|
| 11 |
-
|
| 12 |
-
Recurrent neural networks, also known as RNNs, are a class of neural networks that allow previous outputs to be used as
|
| 13 |
-
inputs while having hidden states. They are typically as follows:
|
| 14 |
-
|
| 15 |
-
.. figure:: ../img/architecture-rnn-ltr.png
|
| 16 |
-
:align: center
|
| 17 |
-
|
| 18 |
-
For each timestep :math:`t` the activation :math:`a^{\langle t \rangle}` and the output :math:`y^{\langle t \rangle}` are expressed as follows:
|
| 19 |
-
|
| 20 |
-
.. math::
|
| 21 |
-
|
| 22 |
-
h^{\langle t \rangle} = g_1\left( W_{hh}h^{\langle t - 1 \rangle} + W_{hx}x^{\langle t \rangle} + b_h \right)
|
| 23 |
-
|
| 24 |
-
y^{\langle t \rangle} = g_2\left( W_{yh}h^{\langle t \rangle} + b_y \right)
|
| 25 |
-
|
| 26 |
-
where :math:`W_{hx}`, :math:`W_{hh}`, :math:`W_{yh}`, :math:`b_h`, :math:`b_y` are coefficients that are shared temporally and :math:`g_1`, :math:`g_2` are activation functions.
|
| 27 |
-
|
| 28 |
-
.. figure:: ../img/description-block-rnn-ltr.png
|
| 29 |
-
:align: center
|
| 30 |
-
|
| 31 |
-
A Python implementation of network above, as an example, could be as follows:
|
| 32 |
-
|
| 33 |
-
.. code-block:: python
|
| 34 |
-
|
| 35 |
-
import numpy as np
|
| 36 |
-
from math import exp
|
| 37 |
-
|
| 38 |
-
np.random.seed(0)
|
| 39 |
-
class VanillaRecurrentNetwork(object):
|
| 40 |
-
|
| 41 |
-
def __init__(self):
|
| 42 |
-
self.hidden_state = np.zeros((3, 3))
|
| 43 |
-
self.W_hh = np.random.randn(3, 3)
|
| 44 |
-
self.W_xh = np.random.randn(3, 3)
|
| 45 |
-
self.W_hy = np.random.randn(3, 3)
|
| 46 |
-
self.Bh = np.random.randn(3,)
|
| 47 |
-
self.By = np.random.rand(3,)
|
| 48 |
-
|
| 49 |
-
self.hidden_state_activation_function = lambda x : np.tanh(x)
|
| 50 |
-
self.y_activation_function = lambda x : x
|
| 51 |
-
|
| 52 |
-
def forward_prop(self, x):
|
| 53 |
-
self.hidden_state = self.hidden_state_activation_function(
|
| 54 |
-
np.dot(self.hidden_state, self.W_hh) + np.dot(x, self.W_xh) + self.Bh
|
| 55 |
-
)
|
| 56 |
-
|
| 57 |
-
return self.y_activation_function(self.W_hy.dot(self.hidden_state) + self.By)
|
| 58 |
-
|
| 59 |
-
Notice the weight matrix above are randomly initialized. This makes it a "silly" network that doesn't help us anything
|
| 60 |
-
good:
|
| 61 |
-
|
| 62 |
-
.. code-block:: python
|
| 63 |
-
|
| 64 |
-
input_vector = np.ones((3, 3))
|
| 65 |
-
silly_network = RecurrentNetwork()
|
| 66 |
-
|
| 67 |
-
# Notice that same input, but leads to different ouptut at every single time step.
|
| 68 |
-
print silly_network.forward_prop(input_vector)
|
| 69 |
-
print silly_network.forward_prop(input_vector)
|
| 70 |
-
print silly_network.forward_prop(input_vector)
|
| 71 |
-
|
| 72 |
-
# this gives us
|
| 73 |
-
[[-1.73665315 -2.40366542 -2.72344361]
|
| 74 |
-
[ 1.61591482 1.45557046 1.13262256]
|
| 75 |
-
[ 1.68977504 1.54059305 1.21757531]]
|
| 76 |
-
[[-2.15023381 -2.41205828 -2.71701457]
|
| 77 |
-
[ 1.71962883 1.45767515 1.13101034]
|
| 78 |
-
[ 1.80488553 1.542929 1.21578594]]
|
| 79 |
-
[[-2.15024751 -2.41207375 -2.720968 ]
|
| 80 |
-
[ 1.71963227 1.45767903 1.13200175]
|
| 81 |
-
[ 1.80488935 1.54293331 1.21688628]]
|
| 82 |
-
|
| 83 |
-
This is because we haven't train our RNN network yet, which we discuss next
|
| 84 |
-
|
| 85 |
-
Training
|
| 86 |
-
--------
|
| 87 |
-
|
| 88 |
-
.. admonition:: Prerequisite
|
| 89 |
-
|
| 90 |
-
We would assume some basic Artificial Neural Network concepts, which are drawn from *Chapter 4 - Artificial Neural
|
| 91 |
-
Networks* (p. 81) of `MACHINE LEARNING by Mitchell, Thom M. (1997)`_ Paperback. Please, if possible, read the
|
| 92 |
-
chapter beforehand and refer to it if something looks confusing in the discussion of this section
|
| 93 |
-
|
| 94 |
-
In the case of a recurrent neural network, we are essentially backpropagation through time, which means that we are
|
| 95 |
-
forwarding through entire sequence to compute losses, then backwarding through entire sequence to compute gradients.
|
| 96 |
-
Formally, the `loss function`_ :math:`\mathcal{L}` of all time steps is defined as the sum of
|
| 97 |
-
the loss at every time step:
|
| 98 |
-
|
| 99 |
-
.. math::
|
| 100 |
-
|
| 101 |
-
\mathcal{L}\left( \hat{y}, y \right) = \sum_{t = 1}^{T_y}\mathcal{L}\left( \hat{y}^{<t>}, y^{<t>} \right)
|
| 102 |
-
|
| 103 |
-
However, this becomes problematic when we want to train a sequence that is very long. For example, if we were to train a
|
| 104 |
-
a paragraph of words, we have to iterate through many layers before we can compute one simple gradient step. In
|
| 105 |
-
practice, for the back propagation, we examine how the output at the very *last* timestep affects the weights at the
|
| 106 |
-
very first time step. Then we can compute the gradient of loss function, the details of which can be found in the
|
| 107 |
-
`Vanilla RNN Gradient Flow & Vanishing Gradient Problem`_
|
| 108 |
-
|
| 109 |
-
.. admonition:: Gradient Clipping
|
| 110 |
-
|
| 111 |
-
Gradient clipping is a technique used to cope with the `exploding gradient`_ problem sometimes encountered when
|
| 112 |
-
performing backpropagation. By capping the maximum value for the gradient, this phenomenon is controlled in
|
| 113 |
-
practice.
|
| 114 |
-
|
| 115 |
-
.. figure:: ../img/gradient-clipping.png
|
| 116 |
-
:align: center
|
| 117 |
-
|
| 118 |
-
In order to remedy the vanishing gradient problem, specific gates are used in some types of RNNs and usually have a
|
| 119 |
-
well-defined purpose. They are usually noted :math:`\Gamma` and are defined as
|
| 120 |
-
|
| 121 |
-
.. math::
|
| 122 |
-
|
| 123 |
-
\Gamma = \sigma(Wx^{<t>} + Ua^{<t - 1>} + b)
|
| 124 |
-
|
| 125 |
-
where :math:`W`, :math:`U`, and :math:`b` are coefficients specific to the gate and :math:`\sigma` is the sigmoid
|
| 126 |
-
function
|
| 127 |
-
|
| 128 |
-
LSTM Formulation
|
| 129 |
-
^^^^^^^^^^^^^^^^
|
| 130 |
-
|
| 131 |
-
Now we know that Vanilla RNN has Vanishing/exploding gradient problem, `LSTM Formulation`_ discusses the theory of LSTM
|
| 132 |
-
which is used to remedy this problem.
|
| 133 |
-
|
| 134 |
-
Applications of RNNs
|
| 135 |
-
--------------------
|
| 136 |
-
|
| 137 |
-
RNN models are mostly used in the fields of natural language processing and speech recognition. The different
|
| 138 |
-
applications are summed up in the table below:
|
| 139 |
-
|
| 140 |
-
.. list-table:: Applications of RNNs
|
| 141 |
-
:widths: 20 60 20
|
| 142 |
-
:align: center
|
| 143 |
-
:header-rows: 1
|
| 144 |
-
|
| 145 |
-
* - Type of RNN
|
| 146 |
-
- Illustration
|
| 147 |
-
- Example
|
| 148 |
-
* - | One-to-one
|
| 149 |
-
| :math:`T_x = T_y = 1`
|
| 150 |
-
- .. figure:: ../img/rnn-one-to-one-ltr.png
|
| 151 |
-
- Traditional neural network
|
| 152 |
-
* - | One-to-many
|
| 153 |
-
| :math:`T_x = 1`, :math:`T_y > 1`
|
| 154 |
-
- .. figure:: ../img/rnn-one-to-many-ltr.png
|
| 155 |
-
- Music generation
|
| 156 |
-
* - | Many-to-one
|
| 157 |
-
| :math:`T_x > 1`, :math:`T_y = 1`
|
| 158 |
-
- .. figure:: ../img/rnn-many-to-one-ltr.png
|
| 159 |
-
- Sentiment classification
|
| 160 |
-
* - | Many-to-many
|
| 161 |
-
| :math:`T_x = T_y`
|
| 162 |
-
- .. figure:: ../img/rnn-many-to-many-same-ltr.png
|
| 163 |
-
- Named entity recognition
|
| 164 |
-
* - | Many-to-many
|
| 165 |
-
| :math:`T_x \ne T_y`
|
| 166 |
-
- .. figure:: ../img/rnn-many-to-many-different-ltr.png
|
| 167 |
-
- Machine translation
|
| 168 |
-
|
| 169 |
-
.. _`exploding gradient`: https://qubitpi.github.io/stanford-cs231n.github.io/rnn/#vanilla-rnn-gradient-flow--vanishing-gradient-problem
|
| 170 |
-
|
| 171 |
-
.. _`MACHINE LEARNING by Mitchell, Thom M. (1997)`: https://a.co/d/bjmsEOg
|
| 172 |
-
|
| 173 |
-
.. _`loss function`: https://qubitpi.github.io/stanford-cs231n.github.io/neural-networks-2/#losses
|
| 174 |
-
.. _`LSTM Formulation`: https://qubitpi.github.io/stanford-cs231n.github.io/rnn/#lstm-formulation
|
| 175 |
-
|
| 176 |
-
.. _`Vanilla RNN Gradient Flow & Vanishing Gradient Problem`: https://qubitpi.github.io/stanford-cs231n.github.io/rnn/#vanilla-rnn-gradient-flow--vanishing-gradient-problem
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lamassu/rnn/example.py
ADDED
|
@@ -0,0 +1,50 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import numpy as np
|
| 2 |
+
|
| 3 |
+
from lamassu.rnn.rnn import Config
|
| 4 |
+
from lamassu.rnn.rnn import RecurrentNeuralNetwork
|
| 5 |
+
|
| 6 |
+
if __name__ == "__main__":
|
| 7 |
+
num_hidden_perceptrons= 100
|
| 8 |
+
seq_length = 25
|
| 9 |
+
learning_rate = 1e-1
|
| 10 |
+
|
| 11 |
+
|
| 12 |
+
data = open('pride-and-prejudice.txt', 'r').read()
|
| 13 |
+
char_set = list(set(data))
|
| 14 |
+
num_chars, num_unique_chars = len(data), len(char_set)
|
| 15 |
+
char_to_idx = { ch:i for i,ch in enumerate(char_set) }
|
| 16 |
+
idx_to_char = { i:ch for i,ch in enumerate(char_set) }
|
| 17 |
+
|
| 18 |
+
rnn = RecurrentNeuralNetwork(
|
| 19 |
+
Config(
|
| 20 |
+
num_hidden_perceptrons=num_hidden_perceptrons,
|
| 21 |
+
input_size=num_unique_chars,
|
| 22 |
+
learning_rate=learning_rate
|
| 23 |
+
)
|
| 24 |
+
)
|
| 25 |
+
|
| 26 |
+
num_iter, pointer = 0, 0
|
| 27 |
+
|
| 28 |
+
|
| 29 |
+
while True:
|
| 30 |
+
if pointer + seq_length + 1 >= len(data) or num_iter == 0:
|
| 31 |
+
prev_history = np.zeros((num_hidden_perceptrons, 1))
|
| 32 |
+
pointer = 0
|
| 33 |
+
input = [char_to_idx[c] for c in data[pointer: pointer + seq_length]]
|
| 34 |
+
target = [char_to_idx[c] for c in data[pointer + 1: pointer + seq_length + 1]]
|
| 35 |
+
|
| 36 |
+
if num_iter % 100 == 0: # inference after every 100 trainings
|
| 37 |
+
inferenced_idxes = rnn.inference(prev_history, input[0])
|
| 38 |
+
inferenced = ''.join(idx_to_char[idx] for idx in inferenced_idxes)
|
| 39 |
+
print("============ inference ============")
|
| 40 |
+
print(inferenced)
|
| 41 |
+
|
| 42 |
+
history, q, x, loss = rnn.forward_pass(input, target, prev_history)
|
| 43 |
+
|
| 44 |
+
if num_iter % 100 == 0:
|
| 45 |
+
print("loss: {}".format(loss))
|
| 46 |
+
|
| 47 |
+
prev_history = rnn.back_propagation(input, target, history, q, x)
|
| 48 |
+
|
| 49 |
+
pointer += seq_length
|
| 50 |
+
num_iter += 1
|
lamassu/rnn/rnn.py
ADDED
|
@@ -0,0 +1,114 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import numpy as np
|
| 2 |
+
from math import exp
|
| 3 |
+
from dataclasses import dataclass
|
| 4 |
+
|
| 5 |
+
|
| 6 |
+
np.random.seed(0)
|
| 7 |
+
|
| 8 |
+
@dataclass
|
| 9 |
+
class Config():
|
| 10 |
+
num_hidden_perceptrons: int
|
| 11 |
+
input_size: int
|
| 12 |
+
learning_rate: float
|
| 13 |
+
|
| 14 |
+
|
| 15 |
+
class RecurrentNeuralNetwork(object):
|
| 16 |
+
"""
|
| 17 |
+
Architecture is single-hidden-layer
|
| 18 |
+
"""
|
| 19 |
+
|
| 20 |
+
def __init__(self, config: Config):
|
| 21 |
+
self.config = config
|
| 22 |
+
|
| 23 |
+
self.W_xh = np.random.randn(config.num_hidden_perceptrons, config.input_size)
|
| 24 |
+
self.W_hh = np.random.randn(config.num_hidden_perceptrons, config.num_hidden_perceptrons)
|
| 25 |
+
self.W_yh = np.random.randn(config.input_size, config.num_hidden_perceptrons)
|
| 26 |
+
|
| 27 |
+
self.b_h = np.zeros((config.num_hidden_perceptrons, 1))
|
| 28 |
+
self.b_o = np.zeros((config.input_size, 1))
|
| 29 |
+
|
| 30 |
+
def forward_pass(self, input, target, prev_history):
|
| 31 |
+
"""
|
| 32 |
+
|
| 33 |
+
:param input: The input vector; each element is an index
|
| 34 |
+
:return:
|
| 35 |
+
"""
|
| 36 |
+
|
| 37 |
+
history, x, o, q, loss = {}, {}, {}, {}, 0
|
| 38 |
+
history[-1] = np.copy(prev_history)
|
| 39 |
+
|
| 40 |
+
for t in range(len(input)):
|
| 41 |
+
x[t] = np.zeros((self.config.input_size, 1))
|
| 42 |
+
x[t][input[t]] = 1
|
| 43 |
+
|
| 44 |
+
if t == 0:
|
| 45 |
+
np.dot(self.W_hh, history[t - 1])
|
| 46 |
+
np.dot(self.W_xh, x[t])
|
| 47 |
+
|
| 48 |
+
history[t] = np.tanh(
|
| 49 |
+
np.dot(self.W_hh, history[t - 1]) + np.dot(self.W_xh, x[t]) + self.b_h
|
| 50 |
+
)
|
| 51 |
+
o[t] = np.dot(self.W_yh, history[t]) + self.b_o
|
| 52 |
+
q[t] = np.exp(o[t]) / np.sum(np.exp(o[t]))
|
| 53 |
+
loss += -np.log(q[t][target, 0])
|
| 54 |
+
|
| 55 |
+
return history, q, x, loss
|
| 56 |
+
|
| 57 |
+
def back_propagation(self, input, target, history, q, x):
|
| 58 |
+
gradient_loss_over_W_xh = np.zeros_like(self.W_xh)
|
| 59 |
+
gradient_loss_over_W_hh = np.zeros_like(self.W_hh)
|
| 60 |
+
gradient_loss_over_W_yh = np.zeros_like(self.W_yh)
|
| 61 |
+
|
| 62 |
+
gradient_loss_over_b_h = np.zeros_like(self.b_h)
|
| 63 |
+
gradient_loss_over_b_y = np.zeros_like(self.b_o)
|
| 64 |
+
|
| 65 |
+
gradient_loss_over_next_h = np.zeros_like(history[0])
|
| 66 |
+
|
| 67 |
+
for t in reversed(range(len(input))):
|
| 68 |
+
gradient_loss_over_o = np.copy(q[t])
|
| 69 |
+
gradient_loss_over_o[target[t]] -= 1
|
| 70 |
+
|
| 71 |
+
gradient_loss_over_W_yh += np.dot(gradient_loss_over_o, history[t].T)
|
| 72 |
+
gradient_loss_over_b_y += gradient_loss_over_o #
|
| 73 |
+
|
| 74 |
+
gradient_loss_over_h = np.dot(self.W_yh.T, gradient_loss_over_o) + gradient_loss_over_next_h
|
| 75 |
+
diag_times_gradient_loss_over_h = (1 - history[t] * history[t]) * gradient_loss_over_h
|
| 76 |
+
|
| 77 |
+
gradient_loss_over_b_h += diag_times_gradient_loss_over_h #
|
| 78 |
+
|
| 79 |
+
gradient_loss_over_W_xh += np.dot(diag_times_gradient_loss_over_h, x[t].T) #
|
| 80 |
+
gradient_loss_over_W_hh += np.dot(diag_times_gradient_loss_over_h, history[t - 1].T) #
|
| 81 |
+
|
| 82 |
+
gradient_loss_over_next_h = np.dot(self.W_hh.T, diag_times_gradient_loss_over_h)
|
| 83 |
+
|
| 84 |
+
for gradient in [gradient_loss_over_W_xh, gradient_loss_over_W_hh, gradient_loss_over_W_yh, gradient_loss_over_b_h, gradient_loss_over_b_y]:
|
| 85 |
+
np.clip(gradient, -5, 5, out=gradient) # avoid exploding gradients
|
| 86 |
+
|
| 87 |
+
# update weights
|
| 88 |
+
for param, gradient in zip(
|
| 89 |
+
[self.W_xh, self.W_hh, self.W_yh, self.b_h, self.b_o],
|
| 90 |
+
[gradient_loss_over_W_xh, gradient_loss_over_W_hh, gradient_loss_over_W_yh, gradient_loss_over_b_h, gradient_loss_over_b_y]):
|
| 91 |
+
param += -self.config.learning_rate * gradient
|
| 92 |
+
|
| 93 |
+
return history[len(input) - 1]
|
| 94 |
+
|
| 95 |
+
def inference(self, history, seed_idx):
|
| 96 |
+
x = np.zeros((self.config.input_size, 1))
|
| 97 |
+
x[seed_idx] = 1
|
| 98 |
+
idxes = []
|
| 99 |
+
|
| 100 |
+
for timestep in range(200):
|
| 101 |
+
history = np.tanh(np.dot(self.W_xh, x) + np.dot(self.W_hh, history) + self.b_h)
|
| 102 |
+
o = np.dot(self.W_yh, history) + self.b_o
|
| 103 |
+
p = np.exp(o) / np.sum(np.exp(o))
|
| 104 |
+
|
| 105 |
+
next_idx = self._inference_single(p.ravel())
|
| 106 |
+
|
| 107 |
+
x[next_idx] = 1
|
| 108 |
+
idxes.append(next_idx)
|
| 109 |
+
|
| 110 |
+
return idxes
|
| 111 |
+
|
| 112 |
+
|
| 113 |
+
def _inference_single(self, probability_distribution):
|
| 114 |
+
return np.random.choice(range(self.config.input_size), p=probability_distribution)
|
lamassu/rnn/vanilla.py
DELETED
|
@@ -1,25 +0,0 @@
|
|
| 1 |
-
import numpy as np
|
| 2 |
-
from math import exp
|
| 3 |
-
|
| 4 |
-
np.random.seed(0)
|
| 5 |
-
class VanillaRecurrentNetwork(object):
|
| 6 |
-
|
| 7 |
-
def __init__(self):
|
| 8 |
-
self.hidden_state = np.zeros((3, 3))
|
| 9 |
-
self.W_hh = np.random.randn(3, 3)
|
| 10 |
-
self.W_xh = np.random.randn(3, 3)
|
| 11 |
-
self.W_hy = np.random.randn(3, 3)
|
| 12 |
-
self.Bh = np.random.randn(3,)
|
| 13 |
-
self.By = np.random.rand(3,)
|
| 14 |
-
|
| 15 |
-
self.hidden_state_activation_function = lambda x : np.tanh(x)
|
| 16 |
-
self.y_activation_function = lambda x : x
|
| 17 |
-
|
| 18 |
-
self.loss_funciton = lambda y : exp(y) / np.sum(exp(y))
|
| 19 |
-
|
| 20 |
-
def forward_prop(self, x):
|
| 21 |
-
self.hidden_state = self.hidden_state_activation_function(
|
| 22 |
-
np.dot(self.hidden_state, self.W_hh) + np.dot(x, self.W_xh) + self.Bh
|
| 23 |
-
)
|
| 24 |
-
|
| 25 |
-
return self.y_activation_function(self.W_hy.dot(self.hidden_state) + self.By)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
setup.py
CHANGED
|
@@ -2,7 +2,7 @@ from setuptools import setup, find_packages
|
|
| 2 |
|
| 3 |
setup(
|
| 4 |
name="lamassu",
|
| 5 |
-
version="0.0.
|
| 6 |
description="Empowering individual to agnostically run machine learning algorithms to produce ad-hoc AI features",
|
| 7 |
url="https://github.com/QubitPi/lamassu",
|
| 8 |
author="Jiaqi liu",
|
|
|
|
| 2 |
|
| 3 |
setup(
|
| 4 |
name="lamassu",
|
| 5 |
+
version="0.0.12",
|
| 6 |
description="Empowering individual to agnostically run machine learning algorithms to produce ad-hoc AI features",
|
| 7 |
url="https://github.com/QubitPi/lamassu",
|
| 8 |
author="Jiaqi liu",
|