description
stringlengths 38
154k
| category
stringclasses 5
values | solutions
stringlengths 13
289k
| name
stringlengths 3
179
| id
stringlengths 24
24
| tags
listlengths 0
13
| url
stringlengths 54
54
| rank_name
stringclasses 8
values |
|---|---|---|---|---|---|---|---|
R, a programming language used for Statistics and Data Analysis, has the function `rank`, which returns the rank for each value in a vector.
For example:
```
my_arr = [1, 3, 3, 9, 8]
# Ranked would be: [0, 1.5, 1.5, 4, 3]
```
When two or more values have the same rank, they are assigned the mean of their rankings. Here, the two `3`s have ranks `1` and `2`, so both are assigned rank `1.5`.
Implement the function `rank()` so that it works the same it does in R.
### Examples
```
[9, 1, 4, 5, 4] ➞ [4.0, 0.0, 1.5, 3.0, 1.5]
["z", "c", "f", "b", "c"] ➞ [4.0, 1.5, 3.0, 0.0, 1.5]
```
### Notes
- Expect numbers and lower-case alphabetic characters only.
- Vectors in R are similar to an array. Although vectors in R are 1-indexed, your function should be 0-indexed. Other differences between vectors and arrays will be ignored for the scope of this challenge.
- 0 <= len(lst) <= 10^4
|
games
|
def rank(lst):
p = {}
for i, v in enumerate(sorted(lst)):
p . setdefault(v, []). append(i)
return [sum(p[v]) / len(p[v]) for v in lst]
|
Sorting in R: Rank
|
65006177f534f65b2594df05
|
[
"Lists",
"Puzzles",
"Sorting"
] |
https://www.codewars.com/kata/65006177f534f65b2594df05
|
7 kyu
|
**Task**
Given a list of values, return a list with each value replaced with the empty value of the same type.
**More explicitly**
- Replace integers `(e.g. 1, 3)`, whose type is int, with `0`
- Replace floats `(e.g. 3.14, 2.17)`, whose type is float, with `0.0`
- Replace strings `(e.g. "abcde", "x")`, whose type is str, with `""`
- Replace booleans `(True, False)`, whose type is bool, with `False`
- Replace lists `(e.g. [1, "a", 5], [[4]])`, whose type is list, with `[]`
- Replace tuples `(e.g. (1,9,0), (2,))`, whose type is tuple, with `()`
- Replace dictionaries `(e.g. {29: 11, 24: 63})`, whose type is dictionary, with `{}`
- Replace sets `(e.g. {0,"a"}, {"b"})`, whose type is set, with `set()`
- Caution: Python interprets `{}` as the empty dictionary, **not** the empty set.
- `None`, whose type is NoneType, is preserved as None
**Examples**
```
[1, 2, 3] ➞ [0, 0, 0]
[7, 3.14, "cat"] ➞ [0, 0.0, ""]
[[1, 2, 3], (1,2,3), {1,2,3}] ➞ [[], (), set()]
[[7, 3.14, "cat"]] ➞ [[]]
[{}] ➞ [{}]
[None] ➞ [None]
```
**Notes**
`None` has the special `NoneType` all for itself.
|
reference
|
def empty_values(lst):
return [type(x)() for x in lst]
|
Emptying the Values
|
650017e142964e000f19cac3
|
[] |
https://www.codewars.com/kata/650017e142964e000f19cac3
|
7 kyu
|
In this challenge you will be given a list similar to the following:
```
[[3], 4, [2], [5], 1, 6]
```
In words, elements of the list are either an integer or a list containing a single integer. If you try to sort this list via sorted([[3], 4, [2], [5], 1, 6]), Python will whine about not being able to compare integers and lists.
However, us humans can clearly see that this list can reasonably be sorted according to "the content of the elements" as:
```
[1, [2], [3], 4, [5], 6]
```
Create a function that, given a list similar to the above, sorts the list according to the "content of the elements".
**Examples**
```
[4, 1, 3] ➞ [1, 3, 4]
[[4], [1], [3]] ➞ [[1], [3], [4]]
[4, [1], 3] ➞ [[1], 3, 4]
[[4], 1, [3]] ➞ [1, [3], [4]]
[[3], 4, [2], [5], 1, 6] ➞ [1, [2], [3], 4, [5], 6]
```
**Notes**
- To reiterate, elements of the list will be either integers or lists with a single integer.
- All numbers will be unique. (you will not get lists like [1, [1]] etc.)
|
reference
|
def sort_it(array):
return sorted(array, key=lambda x: x[0] if isinstance(x, list) else x)
|
Sort the Unsortable
|
65001dd40038a647480989c8
|
[
"Algorithms",
"Arrays",
"Sorting",
"Lists"
] |
https://www.codewars.com/kata/65001dd40038a647480989c8
|
7 kyu
|
**Task**
Create a function that calculates the **count of n-digit** strings with the same sum for the first half and second half of their digits. These digits are referred to as "lucky" digits.
**Examples**
```
Input: 2 ➞ Output: 10
# "00", "11", "22", "33", "44", "55", "66", "77", "88", "99"
Input: 4 ➞ Output: 670
Input: 6 ➞ Output: 55252
# "000000", "001010", "112220", ..., "999999"
```
**Notes**
- The value of `n` will always be even.
- 2 <= n <= 150
- To avoid hard-coding, your code limit should be <= 250 characters
|
algorithms
|
from math import comb
# https://oeis.org/A174061
def lucky_ticket(n):
return sum((- 1) * * k * comb(n, k) * comb(n / / 2 * 11 - 10 * k - 1, n - 1) for k in range(n >> 1))
|
Digits of Lucky Tickets
|
64ffefcb3ee338415ec426c1
|
[
"Performance",
"Combinatorics"
] |
https://www.codewars.com/kata/64ffefcb3ee338415ec426c1
|
6 kyu
|
### Task
Heading off to the **Tree Arboretum of Various Heights**, I bring along my camera to snap up a few photos. Ideally, I'd want to take a picture of as many trees as possible, but the taller trees may cover up the shorter trees behind it.
A tree is hidden if it is **shorter than** or the **same height as** a ( any ) tree in front of it, as seen in a particular direction.
Given a list of tree heights, create a function which returns `"left"` or `"right"`, depending on which side allows me to see as many trees as possible.
### Worked Example
```
[1, 3, 1, 6, 5] ➞ "left"
// If I stand on the left, I can see trees of heights 1, 3 and 6.
// If I stand on the right, I can see trees of heights 5 and 6.
// Return "left" because I would see more trees.
```
### Examples
```
[5, 6, 5, 4] ➞ "right"
[1, 2, 3, 3, 3, 3, 3] ➞ "left"
[3, 1, 4, 1, 5, 9, 2, 6] ➞ "left"
```
### Notes
There will always be a best side.
|
games
|
from math import inf
def tree_photography(lst):
a, b = count(lst), count(reversed(lst))
return 'left' if a > b else 'right'
def count(it):
n, m = 0, - inf
for v in it:
if v > m:
n, m = n + 1, v
return n
|
Tree Photography
|
64fd5072fa88ae669bf15342
|
[
"Arrays",
"Algorithms"
] |
https://www.codewars.com/kata/64fd5072fa88ae669bf15342
|
7 kyu
|
# Task
My friend Nelson loves number theory, so I decide to play this game with him. I have a hidden integer `$ N $`, that might be very large (perhaps even up to `$ 10^{10^{12}} $` :D ).
In one turn, Nelson can ask me one question: he can choose a prime integer `$ p $` and a nonnegative integer `$ e $` and I will tell him whether `$ k = p^e $` is a factor of `$ N $` or not. You may ask this question as many times as you want.
To win the game, Nelson must tell me how many pairs of integers `$ (a, b) $` exist that satisfy the following conditions:
- `$ ab = N $`
- `$ \gcd (a, b) \gt 1 $`
You are Nelson. Please devise an algorithm to win the game in time!
# Constraints
Let `$ N $` be written in terms of its prime factorisation. That is:
```math
N = p_1^{e_1} \cdot p_2^{e_2} \dots p_n^{e_n}
```
It is guaranteed that: `$ 1 \le n \le 400$`, `$ 2 \le p_i \le 10^5 $`, `$ 1 \le e_i \le 10^9 $` per test, and the number of tests does not exceed `$ 610 $`.
# Input / Output
You must code a function `play(query)` - that is, you are given the `query` function as a parameter. The `query` function accepts two `int`, where the first is a prime number `$ p $` and the second is a nonnegative integer `$ e $` such that `$ p^e = k $`. It will return a boolean `True` if `$ k $` is a factor of `$ N $`, and `False` otherwise, or if `$ p $` is not prime. You must return an `int` from your function `play` which is the answer to the question.
# Example Interaction
Suppose the hidden number `$ N = 84 $`. Here's an example of how the game might go:
- First, Nelson asks me whether `$ 8 $` is a factor of `$ N $`. That is, your code calls the function `query(2, 3)`. My response is 'No', and so `query(2, 3)` will return `false`/`False`
- Next, Nelson asks me whether `$ 7 $` is a factor of `$ N $`. That is, your code calls the function `query(7, 1)`. My response is 'Yes', and so `query(7, 1)` will return `true`/`True`
- Suppose Nelson asks a few more questions and somehow figures out the answer to the question. He tells me with conviction, 'The answer is `$ 4 $`', and he wins the game. That is, if your function returns `4` you pass this test, and you fail this test otherwise.
The `$ 4 $` pairs of `$ (a, b) $` are listed below:
- `$ (2, 42) $`
- `$ (6, 14) $`
- `$ (14, 6) $`
- `$ (42, 2) $`
# Tests
Your code will be tested on 10 sample tests and 600 random tests.
|
games
|
from math import prod
PRIMES = [n for n in range(2, 10 * * 5 + 1) if all(n % p for p in range(2, int(n * * .5) + 1))]
def play(query):
z = {}
for p in PRIMES:
if not query(p, 1):
continue
l, r = 1, 10 * * 9 + 1
while r - l > 1:
m = (r + l) / / 2
if query(p, m):
l = m
else:
r = m
if l:
z[p] = l
return prod(v + 1 for v in z . values()) - 2 * * len(z)
|
Nelson the Number Theorist
|
64fb5c7a18692c0876ebbac8
|
[
"Number Theory",
"Mathematics",
"Performance"
] |
https://www.codewars.com/kata/64fb5c7a18692c0876ebbac8
|
4 kyu
|
You will be given an array of numbers which represent your character's **altitude** above sea level at regular intervals:
* Positive numbers represent height above the water.
* 0 is sea level.
* Negative numbers represent depth below the water's surface.
**Create a function which returns whether your character survives their unsupervised diving experience, given an array of integers.**
1. Your character starts with a **breath meter of 10**, which is the maximum. When diving underwater, your breath meter **decreases by 2** per item in the array. Watch out! If your breath **diminishes to 0**, your character dies!
2. To prevent this, you can **replenish your breath by 4 (up to the maximum of 10)** for each item in the array where you are at or above sea level.
3. Your function should return `True` if your character survives, and `False` if not.
### Worked Example
```
[-5, -15, -4, 0, 5] ➞ True
// Breath meter starts at 10.
// -5 is below water, so breath meter decreases to 8.
// -15 is below water, so breath meter decreases to 6.
// -4 is below water, so breath meter decreases to 4.
// 0 is at sea level, so breath meter increases to 8.
// 5 is above sea level and breath meter is capped at 10 (would've been 12 otherwise).
// Character survives!
```
### Examples
```
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10] ➞ True
[-3, -6, -2, -6, -2] ➞ False
[2, 1, 2, 1, -3, -4, -5, -3, -4] ➞ False
```
### Notes
* Lists may be of any length.
* All arrays are valid.
|
games
|
def diving_minigame(lst):
breath_meter = 10
for x in lst:
if x < 0:
breath_meter -= 2
else:
breath_meter = min(10, breath_meter + 4)
if breath_meter <= 0:
return False
return True
|
Hold Your Breath!
|
64fbfa3518692c2ed0ebbaa2
|
[
"Lists",
"Puzzles"
] |
https://www.codewars.com/kata/64fbfa3518692c2ed0ebbaa2
|
7 kyu
|
Let's say that there exists a machine that gives out free coins, but with a twist!
Separating two people is a wall, and this machine is placed in such a way that both people are able to access it. Spending a coin in this machine will give the person on the other side **3 coins** and vice versa.
If both people continually spend coins for each other (SHARING), then they'll both gain a net profit of **2 coins per turn.** However, there is always the possibility for someone to act selfishly (STEALING): they spend no coins, yet they still receive the generous **3 coin** gift from the other person!
*Here's an example of Red taking advantage of Green!*

### The Challenge
Assuming that both people **start with 3 coins each**, create a function that calculates both people's final number of coins. You will be given two arrays of strings, with each string being the words `"share"` or `"steal"`.
### Examples
```
["share"], ["share"] ➞ (5, 5)
// Both people spend one coin, and receive 3 coins each.
["steal"], ["share"] ➞ (6, 2)
// Person 1 gains 3 coins, while person 2 loses a coin.
["steal"], ["steal"] ➞ (3, 3)
// Neither person spends any coins and so no one gets rewarded.
["share", "share", "share"], ["steal", "share", "steal"] ➞ (3, 11)
```
### Notes
- No tests will include a negative number of coins.
- All words will be given in lowercase.
|
reference
|
def get_coin_balances(lst1, lst2):
x, y = lst1 . count("share"), lst2 . count("share")
return 3 - x + 3 * y, 3 - y + 3 * x
|
Coin Co-Operation
|
64fc00392b610b1901ff0f17
|
[] |
https://www.codewars.com/kata/64fc00392b610b1901ff0f17
|
7 kyu
|
### Task
Given a string, return if all occurrences of a given letter are always immediately followed by the other given letter.
### Worked Example
```
("he headed to the store", "h", "e") ➞ True
# All occurences of "h": ["he", "headed", "the"]
# All occurences of "h" have an "e" after it.
# Return True
('abcdee', 'e', 'e') ➞ False
# For first "e" we can get "ee"
# For second "e" we cannot have "ee"
# Return False
```
### Examples
```
("i found an ounce with my hound", "o", "u") ➞ True
("we found your dynamite", "d", "y") ➞ False
```
### Notes
- All sentences will be given in lowercase.
|
reference
|
def best_friend(t, a, b):
return t . count(a) == t . count(a + b)
|
A Letter's Best Friend
|
64fc03a318692c1333ebc04c
|
[
"Fundamentals",
"Strings"
] |
https://www.codewars.com/kata/64fc03a318692c1333ebc04c
|
7 kyu
|
### Task
Create a function that always returns `True`/`true` for every item in a given list.
However, if an element is the word **'flick'**, switch to always returning the opposite boolean value.
### Examples
```python
['codewars', 'flick', 'code', 'wars'] ➞ [True, False, False, False]
['flick', 'chocolate', 'adventure', 'sunshine'] ➞ [False, False, False, False]
['bicycle', 'jarmony', 'flick', 'sheep', 'flick'] ➞ [True, True, False, False, True]
```
### Notes
- "flick" will always be given in lowercase.
- A list may contain multiple flicks.
- Switch the boolean value on the same element as the flick itself.
|
reference
|
def flick_switch(lst):
res, state = [], True
for i in lst :
if i == 'flick' :
state = not state
res . append ( state )
return res
|
Flick Switch
|
64fbfe2618692c2018ebbddb
|
[
"Fundamentals",
"Lists"
] |
https://www.codewars.com/kata/64fbfe2618692c2018ebbddb
|
8 kyu
|
### Task
A new 'hacky' phone is launched, which has the feature of connecting to any Wi-Fi network from any distance away, as long as there aren't any obstructions between the hotspot and the phone. Given a string, return how many Wi-Fi hotspots I'm able to connect to.
* The phone is represented as a `P`.
* A hotspot is represented as an `*`.
* An obstruction is represented as a `#`. You cannot access a hotspot if they are behind one of these obstructions.
### Examples
```
"* P * *" ➞ 3
# No obstructions
"* * # * P # * #" ➞ 1
# Only one wifi available before obstructions
nonstopHotspot("***#P#***") ➞ 0
# No access due to obstructions
```
### Notes
* There will be only one phone.
* No other characters, other than spaces, will appear in the tests.
|
games
|
import re
def nonstop_hotspot(area):
ans = re . search(r'[* ]*P[* ]*', area)
return ans . group(). count('*')
|
Get Free Wi-Fi Anywhere You Go
|
64fbf7eb2b610b1a6eff0e44
|
[
"Algorithms",
"Puzzles",
"Strings"
] |
https://www.codewars.com/kata/64fbf7eb2b610b1a6eff0e44
|
7 kyu
|
# It's Raining Tacos!
A line of tacos is falling out of the sky onto the landscape.
Your task is to predict what the landscape will look like when the tacos fall on it.
```
INPUT:
*********
```
```
OUTPUT: TACOTACOT
*********
```
The landscape is represented as any ASCII character, with the air being represented as whitespaces. The rows are separated by newline characters.
Tacos fall from left to right, distributing the word `TACO` repeadetly over the landscape. Each letter falls on the topmost part of the landscape in that area.
If there are no characters in that location, the taco falls all the way to the bottom.
```
INPUT: * **
*** ****
```
```
C AC
OUTPUT: TA* T**O
***O****T
```
If there is no space for tacos to fall, then that space is skipped. The next letter still continues forward in the `TACO` sequence.
```
**
INPUT: ****
******
```
```
**CO
OUTPUT: ****TA
******COT
```
Tacos cannot fall through solid material. If there is a floating island, `TACO` should be placed on the island, not below it.
```
INPUT: *****
```
```
COTAC
OUTPUT: *****
TA OT
```
The width and height of the landscape can be anywhere from 1 to 100.
In the case of an empty string, return an empty string.
Good Luck!
|
algorithms
|
def rain_tacos(landscape, word='TACO'):
n = len(grid := landscape . splitlines())
grid = [('' . join(row). rstrip() + word[i % len(word)]). ljust(n, ' ')[: n]
for i, row in enumerate(zip(* grid[:: - 1]))]
return '\n' . join(map('' . join, list(zip(* grid))[:: - 1]))
|
It's Raining Tacos
|
64f4ef596f222e004b877272
|
[
"Algorithms"
] |
https://www.codewars.com/kata/64f4ef596f222e004b877272
|
6 kyu
|
# Task
Imagine you have a list of integers. You start at the first item and use each value as a guide to decide where to go next.
Create a function that determines whether the input list forms a complete cycle or not.

# Examples
```
[1, 4, 3, 0, 2] ➞ True
# When you follow the list [1, 4, 3, 0, 2] as shown in the image,
# you visit every item once and return to the starting point, making it a "full cycle."
[1, 4, 0, 3, 2] ➞ False
[5, 3, 4, 2, 0, 1] ➞ True
```
# Notes
- The list will not contain any duplicate values.
- All values are less than the length of the list (i.e., they are valid indices).
- 2 <= len(lst) <= 100
|
reference
|
def full_cycle(lst):
return all((x := lst[i and x]) for i in range(len(lst) - 1))
|
Is This a Full Cycle?
|
64f41ad92b610b64c1067590
|
[
"Arrays"
] |
https://www.codewars.com/kata/64f41ad92b610b64c1067590
|
7 kyu
|
# Perfect Binary Tree Traversal:
In [tree traversal](https://en.wikipedia.org/wiki/Tree_traversal), there are two well-known methods:
* Breadth-First Search (BFS)
* Deep-First Search (DFS)
And we are going to find out some relationship between them.
___
# Perfect Binary Tree:
A perfect binary tree is a special binary tree, all nodes of it have 2 children except the last level.
So a perfect binary tree has the height of 3 looks like:
```
X is a node
X
/ \
/ \
X X
/ \ / \
X X X X
```
___
# Breadth-First Search:
In BFS, you will visit all the nodes of a specific depth, _from left to right_, before you move onto the next depth.
For example:
```
height = 3
1
/ \
/ \
2 3
/ \ / \
4 5 6 7
```
___
# Deep-First Search:
There are 3 methods of DFS: `pre-order`, `in-order` and `post-order`.
(Please note that the sequence is from left to right)
For `pre-order` DFS, you will:
1. Visit the current node
2. Recursively traverse the current node's left subtree
3. Recursively traverse the current node's right subtree
For `in-order` DFS, you will:
1. Recursively traverse the current node's left subtree
2. Visit the current node
3. Recursively traverse the current node's right subtree
For `post-order` DFS, you will:
1. Recursively traverse the current node's left subtree
2. Recursively traverse the current node's right subtree
3. Visit the current node
For example:
```
height = 3
pre-order in-order post-order
1 4 7
/ \ / \ / \
/ \ / \ / \
2 5 2 6 3 6
/ \ / \ / \ / \ / \ / \
3 4 6 7 1 3 5 7 1 2 4 5
```
___
# Task:
Given 2 numbers: `height` of a perfect binary tree and `num`-th node visited in BFS.
Return a tuple of the numbers, which are the sequence of the same node being visited in pre-order, in-order and post-order DFS.
___
# Sample Tests:
height, num => (pre-order, in-order, post-order)
```
2, 1 => (1, 2, 3)
2, 2 => (2, 1, 1)
2, 3 => (3, 3, 2)
3, 1 => (1, 4, 7)
3, 2 => (2, 2, 3)
3, 3 => (5, 6, 6)
3, 4 => (3, 1, 1)
3, 5 => (4, 3, 2)
3, 6 => (6, 5, 4)
3, 7 => (7, 7, 5)
```
___
_NOTE:_
The height will go up to `30`, building up the tree then do BFS and DFS would be very likely to time out.
|
games
|
def convert_number(height, num):
pre = 1
inoreder = 2 * * (height - 1)
post = (2 * * height) - 1
depth = 1
while 2 * * depth <= num:
depth += 1
while depth > 1:
height -= 1
depth -= 1
if 2 * * (depth - 1) & num != 0:
pre += 2 * * height
inoreder += 2 * * (height - 1)
post -= 1
else:
pre += 1
inoreder -= 2 * * (height - 1)
post -= 2 * * height
return pre, inoreder, post
|
Perfect Binary Tree Traversal: BFS to DFS
|
64ebbfc4f1294ff0504352be
|
[
"Algorithms",
"Binary",
"Data Structures",
"Mathematics",
"Trees"
] |
https://www.codewars.com/kata/64ebbfc4f1294ff0504352be
|
5 kyu
|
# Task
Initially, the string consists of a single character. There are two operations:
- `Copy` the entire string into a buffer. It is not allowed to copy a part of the current string.
- `Paste` the buffer content at the end of the string. The string length increases.
Each operation counts as one.
The function is given n the length of the required string. Determine the minimum number of operations needed to make the resulting string exactly of length n.
# Examples
```python
1 ➞ 0
# The string is already of the required length
2 ➞ 2
# Copy, Paste -> 2 operations
3 ➞ 3
# Copy, Paste, Paste -> 3 operations
5 ➞ 5
# Copy, Paste, Paste, Paste, Paste -> 5 operations
8 ➞ 6
# Copy, Paste, Copy, Paste, (the length is 4), Copy, Paste -> 6 operations
9 ➞ 6
# Copy, Paste, Paste, (the length is 3), Copy, Paste, (the length is 6), Paste -> 6 operations
```
# Notes
- The given range is 1 <= n < 2^21.
|
reference
|
from gmpy2 import next_prime
def min_ops(n):
k, p = 0, 2
while n > 1:
while n % p:
p = next_prime(p)
n / /= p
k += p
return k
|
Minimum Number of Copy / Paste Operations
|
64f04307c6307f003106ac2c
|
[] |
https://www.codewars.com/kata/64f04307c6307f003106ac2c
|
6 kyu
|
The Codewars Council meets at a circular table with `n` seats. Depending on the day `d` of the month, `d` people will be chosen as leaders of the council. These `d` leaders are spaced equidistantly from each other on the table, like spokes on a wheel. The leaders are chosen based on which grouping of `d` equidistant people have the largest summed honor. The honor of the participants for that day in the Council is given in an array `arr` of length `n`. Return the combined honor of the `d` leaders of the Council.
Given conditions -
* `n % d == 0`, ie. there will be no invalid cases. All groupings go fully around the circle.
* `1 <= d <= 31`, as you can't have 32 days in a month.
* `n > 0` because you can't have a Council of 0 people. (You also can't have a table with 0 open seats, then it's just a nightstand or something)
* You can have negative honor on Codewars (but it is hard to do) and the solution may be negative.
Example -
```
[1, 2, 3, 4], 2 -> 6 because max(1+3, 2+4) == 6
[1, 5, 6, 3, 4, 2], 3 -> 11 because max(1+6+4, 5+3+2) == 11
[1, 1, 0], 1 -> 1 because max(1, 1, 0) == 1
```
Hint -
Something important to note is that you (usually) don't have to evaluate every sum in the array, as after `n/d` repetitions the sums loop over on themselves.
|
algorithms
|
def largest_radial_sum(arr, d):
return max(sum(arr[i:: len(arr) / / d]) for i in range(len(arr) / / d))
|
Largest Radial Sum
|
64edf7ab2b610b16c2067579
|
[
"Arrays",
"Algorithms"
] |
https://www.codewars.com/kata/64edf7ab2b610b16c2067579
|
6 kyu
|
## Preamble
In Microsoft FreeCell (shipped with early Windows versions), each deal is generated by PRNG seeded by the deal number (see pseudocode below). There are 32000 deals numbered from 1 to 32000. This guarantees every deal is unique, but they are portable across computers, so #1 on one machine is exactly the same on other machines.
## Your task
Your task is to implement the function which accepts a deal number (`1 <= n <= 32000`) and returns an array/list/table (depending on programming language) of the cards corresponding to the given deal. See the dealing process below.
## Initial deck
The initial deck is preloaded in `DECK` constant or variable (see example solution). It's array/list/table of 52 2-character strings (in the table below they are separated by spaces and not enclosed to quotes for readability purpose):
```
AC AD AH AS 2C 2D 2H 2S 3C 3D 3H 3S 4C
4D 4H 4S 5C 5D 5H 5S 6C 6D 6H 6S 7C 7D
7H 7S 8C 8D 8H 8S 9C 9D 9H 9S TC TD TH
TS JC JD JH JS QC QD QH QS KC KD KH KS
```
## Pseudo random number generator
The algorithm used for shuffling the deck is linear congruential generator from early Microsoft C compiler, in pseudocode:
```
state = deal_number
loop {
state = (state * 214013 + 2531011) mod 2^31
next_value = floor[state / 2^16]
}
```
## Dealing process
1. Seed PRNG with the deal number.
2. Take initial deck (see above) and use it for dealing cards. Initial indices are from 0 to 51.
3. While the deck is not empty, do the following operations:
* Generate next random number.
* Choose the card index = `random number` mod `remaining deck length`.
* If it's not the last card of the deck, swap the last card with the card at corresponding index of the deck.
* Remove this card from the deck and deal it (put it on the table).
* Repeat this procedure until all 52 cards are dealt.
For the simplicity, in this kata the table is represented by one dimentional array/list rather than 8 columns like in real FreeCell, in order the cards were placed (first row left to right, second row left to right, and so on).
## Dealing process explained
Let's explain how the dealing process works. For example, we will consider the deal number #1.
* Create new PRNG and initialize it with `state = 1` (for other deals, use its number from the function argument instead of 1).
* Make a copy of the initial deck (so the original one can be reused later for more deals).
* Repeat the following steps until the deck is empty:
* Generate new random number using the current state of PRNG. We modify the state variable and prepare it for the next number: `state = (1 * 214013 + 2531011) mod 2^31 = 2745024`. We divide our state by `2^16` (without modifying the state itself) and get integer part of it rounding down, which is `2745024 / 2^16 = 41`.
* Calculate random number mod remaining deck length and take the corresponding card away from the deck, leaving empty the place where it was. In our example, we calculate `(41 mod 52) = 41`, and 41th card is `JD`, we deal this card.
* The card we extracted from the deck was not the last one in the deck, so we get the last card in the deck and put it to the place where our dealt card was. After the first card, our remaining deck will be (we replaced our JD with KS):
```
AC AD AH AS 2C 2D 2H 2S 3C 3D 3H 3S 4C
4D 4H 4S 5C 5D 5H 5S 6C 6D 6H 6S 7C 7D
7H 7S 8C 8D 8H 8S 9C 9D 9H 9S TC TD TH
TS JC(KS)JH JS QC QD QH QS KC KD KH
```
* Repeat the process, let's deal the second card:
* We modify PRNG state again: `state = (2745024 * 214013 + 2531011) mod 2^31 = 1210316419`
* Get the next random number value: `1210316419 / 2^16 = 18467`.
* Calculate `(18467 mod 51) = 5` (becase we have only 51 cards left in the deck, `JD` was removed before).
* Obtain card at index 5 of the deck which is `2D`.
* Extract it from deck and replace with the last card in our deck:
```
AC AD AH AS 2C(KH)2H 2S 3C 3D 3H 3S 4C
4D 4H 4S 5C 5D 5H 5S 6C 6D 6H 6S 7C 7D
7H 7S 8C 8D 8H 8S 9C 9D 9H 9S TC TD TH
TS JC KS JH JS QC QD QH QS KC KD
```
* Repeat this process until we deal the entire deck of 52 cards.
* Return the resulting cards in order we dealt them.
## Example deals
```
Deal #1:
JD 2D 9H JC 5D 7H 7C 5H
KD KC 9S 5S AD QC KH 3H
2S KS 9D QD JS AS AH 3C
4C 5C TS QH 4H AC 4D 7S
3S TD 4S TH 8H 2C JH 7D
6D 8S 8D QS 6C 3D 8C TC
6S 9C 2H 6H
Deal #11982:
AH AS 4H AC 2D 6S TS JS
3D 3H QS QC 8S 7H AD KS
KD 6H 5S 4D 9H JH 9S 3C
JC 5D 5C 8C 9D TD KH 7C
6C 2C TH QH 6D TC 4S 7S
JD 7D 8H 9C 2H QD 4C 5H
KC 8D 2S 3S
```
## Little help for debugging
If you stuck implementing the right PRNG, here is an example of first 52 numbers generated if the PRNG is seeded with 1:
```
41, 18467, 6334, 26500, 19169, 15724, 11478, 29358, 26962, 24464, 5705, 28145, 23281, 16827, 9961, 491, 2995, 11942, 4827, 5436, 32391, 14604, 3902, 153, 292, 12382, 17421, 18716, 19718, 19895, 5447, 21726, 14771, 11538, 1869, 19912, 25667, 26299, 17035, 9894, 28703, 23811, 31322, 30333, 17673, 4664, 15141, 7711, 28253, 6868, 25547, 27644
```
|
reference
|
from preloaded import DECK
def deal(n):
deck = list(DECK)
state = n
dealt_cards = []
while (len(deck) != 0):
state = (state * 214013 + 2531011) % (2 * * 31)
next_value = int(state / (2 * * 16))
card_index = next_value % len(deck)
if card_index != len(deck) - 1:
last_card = deck[- 1]
current_card = deck[card_index]
deck[- 1] = current_card
deck[card_index] = last_card
dealt_cards . append(deck . pop())
return dealt_cards
|
FreeCell Deal Generator
|
64eca9a7bc3127082b0bc7dc
|
[
"Games"
] |
https://www.codewars.com/kata/64eca9a7bc3127082b0bc7dc
|
7 kyu
|
To almost all of us solving sets of linear equations is quite obviously the most exciting bit of linear algebra. Benny does not agree though and wants to write a quick program to solve his homework problems for him. Unfortunately Benny's lack of interest in linear algebra means he has no real clue on how to go about this. Fortunately, you can help him!
Write a method ```solve``` that accepts a list of linear equations that your method will have to solve. The output should be a map (a `Map` object in JavaScript) with a value for each variable in the equations. If the system does not have a unique solution (has infinitely many solutions or is unsolvable), return ```null``` (`None` in python).
For example :
"2x + 4y + 6z = 18"
"3y + 3z = 6"
"x + 2y = z - 3"
should result in a map :
x = 2
y = -1
z = 3
Possible input equations have the following rules:
- Only the plus and minus operators are used on both the left and right hand side of the equation.
- Both sides of the equation can have variables; One variable can appear in multiple terms, on both sides.
- Variable names are strings of arbitrary length.
- All coefficients are integers and generally fall within the range of -150 to 150, with a few ranging from -1000 to 1000. Free terms are integers in range -20000 to 20000.
- Equations do not necessarily have variables.
- Equations have exactly one operator (+ or -) between terms.
Comparisons are performed with accuracy of `1e-6`.
**Note on numerical stability:**
There are many possible ways to solve a system of linear equations. One group of such algorithms is based on reduction and elimination methods. If you are going to use any of these, remember that such algorithms are in general *numerically unstable*, i.e. division operations repeated over and over introduce inaccuracies which accumulate from row to row. As a result it might occur that some value which is expected to be zero is actually larger, for example, `2.5e-10`. Such inaccuracies tend to be bigger in large equation systems, and random tests check systems of up to 26 equations. If it happens that small tests pass for you, and large tests fail, it probably means that you did not account for inaccuracies correctly.
Also note that tests do not depend on any reference solution, so the way how test cases are generated _is numrically stable_ - the only source of inaccuracies is your solution, and you need to account for it.
```if:python
___Note for python users:___
`numpy` module has been disabled, so that the task matches the one of the other languages. There is an anti-cheat measure about that, so you won't be able to import some other modules too (either way, you shouldn't need any module to solve this kata...)
```
```if:scala
___Note for scala users:___
If the supplied equations do not have a solution, or if they have infinitely many solutions, return an empty `Map`
```
|
algorithms
|
from decimal import Decimal as dec, getcontext
import re
getcontext(). prec = 28
def reduced(arr, comparator):
def check_divider(arr, compare):
for i, (x, y) in enumerate(zip(arr, compare)):
try:
if i == 0:
test = x / y
elif x / y != test:
return False
except:
return False
return True
return any(check_divider(arr, compare) for compare in comparator)
def collumn_extract(lst, col_index): return list(zip(* lst))[col_index]
def GaussJordan(x: list[list], y: list):
a = x . copy()
b = y . copy()
dim = len(a[0])
for col in range(dim - 1):
for row in range(1 + col, dim):
if a[row][col] != 0:
if a[col][col] == 0:
a[row], a[col] = a[col], a[row]
b[row], b[col] = b[col], b[row]
else:
divider = a[row][col] / a[col][col]
a[row] = [a[row][collar] - divider * a[col][collar]
for collar in range(dim)]
b[row] = b[row] - divider * b[col]
for row in range(dim):
if [round(elem, 10) for elem in a[row]] == [0] * len(a[row]):
return None
for col in range(dim - 1, - 1, - 1):
for row in range(col - 1, - 1, - 1):
if a[row][col] != 0:
if a[col][col] == 0:
a[row], a[col] = a[col], a[row]
b[row], b[col] = b[col], b[row]
else:
divider = a[row][col] / a[col][col]
a[row] = [a[row][collar] - divider * a[col][collar]
for collar in range(dim)]
b[row] = b[row] - divider * b[col]
try:
return [round(b[i] / a[i][i], 15) for i in range(dim)]
except:
return None
def solve(* equation):
print(equation)
vars = list(sorted(set(re . findall(r'[a-zA-Z]+', " " . join(equation)))))
if len(vars) > len(equation):
return None
comparator = [0] * len(equation)
coeffs = []
for iteration, lines in enumerate(equation):
isolate = re . findall(r'([+\-]?)([0-9]*)([a-zA-Z]*)|(=)', lines)
found = False
coeff = [0] * len(vars)
for sign, coef, var, prob_equal in isolate:
if (sign, coef, var, prob_equal) != ("", "", "", ""):
if (sign, coef, var, prob_equal) == ("", "", "", "="):
found = True
else:
if coef == '':
coef = '1'
if var:
numb = dec(int(sign + coef) if not found else - int(sign + coef))
coeff[vars . index(var)] += dec(numb)
else:
numb = dec(- int(sign + coef) if not found else int(sign + coef))
comparator[iteration] += dec(numb)
coeffs += [coeff]
if len(vars) < len(equation):
reduction = len(equation) - len(vars)
iteration = 0
while reduction != 0:
try:
if reduced(coeffs[iteration], coeffs[: iteration] + coeffs[iteration + 1:]):
coeffs . pop(iteration)
comparator . pop(iteration)
reduction -= 1
else:
iteration += 1
except:
return None
final = {}
res = GaussJordan(coeffs, comparator)
try:
for i in range(len(res)):
final . update({vars[i]: float(res[i])})
except:
return None
return final
|
Linear Equation Solver
|
56d6d927c9ae3f115b0008dd
|
[
"Algorithms",
"Mathematics"
] |
https://www.codewars.com/kata/56d6d927c9ae3f115b0008dd
|
4 kyu
|
Create a function which returns the state of a board after `n` moves. There are different types of blocks on the board, which are represented as strings.
* `>` is a pusher which moves right every turn, and pushes a block to the right if it occupies the same space as it.
* `'#'` is a block which can be pushed by the pusher. If a block is pushed onto another block, then the other block also joins the push chain!
* `'-'` is an empty space, which a block can be pushed into.
Note that the pusher can push any number of blocks at a time, but is always stopped if the push chain hits the end of the list.
### Examples
```python
block_pushing(['-', '>', '#', '-', '#', '-', '-', '-'], 1) ➞ ['-', '-', '>', '#', '#', '-', '-', '-']
block_pushing(['>', '#', '-', '#', '-', '-', '#'], 10) ➞ ['-', '-', '-', '>', '#', '#', '#']
block_pushing(['>', '-', '>', '#', '-', '-', '#', '-'], 2) ➞ ['-', '-', '>', '-', '>', '#', '#', '-']
block_pushing(['>', '>', '>', '-'], 3) ➞ ['-', '>', '>', '>']
```
### Notes
* There may be more than one pusher at a time on the board.
* Pushers are solid blocks, so a push chain of pushers should also stop when hitting the end of the list.
* 5 <= len(lst) <= 500
|
reference
|
import re
def block_pushing(l, n):
s = '' . join(l)
for _ in range(n):
s = re . sub('(>[>#]*)-', lambda g: '-' + g . group(1), s)
return list(s)
|
Block Pusher
|
64e5e192f1294f96fd60a5ae
|
[] |
https://www.codewars.com/kata/64e5e192f1294f96fd60a5ae
|
6 kyu
|
**Task**
Imagine a lively dice game where four friends, affectionately known as `p1, p2, p3, and p4`, come together for an exciting gaming session. Here's how it unfolds: in each round, all players roll a pair of standard six-sided dice.
The player with the lowest total score is promptly eliminated from the game. But what if two or more players happen to share this dubious honor of the lowest score? In such cases, we introduce a tiebreaker: the player among them with the lowest score from their first dice roll gets the boot.
If, despite these measures, we still have players with identical rolls in the exact same order, **all players** should go for another round of rolls. This electrifying process of elimination keeps going until only one player emerges victorious as the undisputed winner.
Given a list of `scores`, documented meticulously in the order of each player's participation in every round, determine and declare the name of the triumphant player who stands as the last one standing.
**Example**
```python
([(6, 2), (4, 3), (3, 4), (5, 4), (3, 5), (1, 5), (4, 3), (1, 5), (1, 5), (5, 6), (2, 2)]) ➞ "p1"
p1 p2 p3 p4
Round 1 -> (6, 2), (4, 3), (3, 4), (5, 4) Player 3 removed.
Round 2 -> (3, 5), (1, 5), (4, 3) Player 2 removed.
Round 3 -> (1, 5), (1, 5) No lowest score; players roll again.
Round 4 -> (5, 6), (2, 2) Player 1 wins!
```
This thrilling game continues until one player emerges as the ultimate champion!
- 4 <= len(scores)
|
games
|
def dice_game(scores):
players = ['p1', 'p2', 'p3', 'p4']
while len(players) > 1:
results = list(zip(players, scores))
scores = scores[len(players):]
results . sort(key=lambda x: (sum(x[1]), x[1][0]))
if results[0][1] != results[1][1]:
players . remove(results[0][0])
return players[0]
|
The Dice Game
|
64e5b47cc065e56fb115a5bf
|
[] |
https://www.codewars.com/kata/64e5b47cc065e56fb115a5bf
|
6 kyu
|
**Task**
This game is played with a random string of digits 0-9. The object is to reduce the string to zero length by removing digits from the left end of the string. Removals are governed by one simple rule. If the leftmost digit is `n`, you can remove up to `n` digits from the left end (inclusive). After doing this the new leftmost digit is reduced by the number of digits removed. If this would cause the leftmost digit to fall to zero or below then the move is not allowed. The final move of reducing the string to zero length must be done by exact count.
The game `"4621"` can be won in one move since there are 4 digits and the leftmost digit is 4. `"6348"` requires two moves to win: remove 2 to get to `"28"`, and remove 2 again to get to `""`. `"12345"` can't be won by any combination of moves.
Devise a function that takes a string and returns the **shortest** sequence of moves that will win the game. If there are ties for the shortest, sort them in ascending order. If the game is unwinnable return `[]`.
**Examples**
```python
solve("4621") ➞ [(4,)]
# Exact count, 4 digits, leftmost is 4.
solve("6348") ➞ [(2, 2)]
solve("65042485") ➞ [(6, 2)]
solve("51416573385334") ➞ [(4, 2, 3, 5)]
# String after each move: "2573385334", "53385334", "55334", ""
solve("38088198647805") ➞ [(1, 5, 1, 7), (3, 3, 1, 7), (3, 3, 5, 3), (3, 4, 3, 4)]
# Four are tied for shortest, sorted ascending.
solve("2177510183994154") ➞ [(2, 1, 5, 3, 3, 2)]
solve("9555267224559216") ➞ []
# No possible solution.
```
**Note**
This game could be made less simple by allowing draws from either end of the string or, perhaps, by making it a 2 player game with the player making the last move being the winner.
|
games
|
def solve(game):
if game[0] == str(len(game)):
return [(int(game[0]),)]
solutions = []
for i in range(1, int(game[0]) + 1):
if i >= len(game):
break
move_made = game[i:]
if int(move_made[0]) <= i:
continue
move_made = str(int(move_made[0]) - i) + move_made[1:]
other_solutions = solve(move_made)
solutions += [(i,) + os for os in other_solutions]
if not solutions:
return []
min_length = min(map(len, solutions))
return [s for s in solutions if len(s) == min_length]
|
The Simple Game
|
64e5bb63c065e575db15a3f1
|
[] |
https://www.codewars.com/kata/64e5bb63c065e575db15a3f1
|
5 kyu
|
# Task
Find pairs of elements from two input lists such that swapping these pairs results in equal sums for both lists. If no such pair exists, return an empty set.
# Input
Two lists of integers, `list1` and `list2`, with the same length.
# Output
A set of tuples, each containing two elements (`num_from_list1, num_from_list2`). These tuples represent the pairs of elements that can be swapped to make the sums of the lists equal.
# Examples
```python
fair_swap([1, 1], [2, 2]) ➞ {(1, 2)}
fair_swap([1, 2], [2, 3]) ➞ {(1, 2), (2, 3)}
fair_swap([2], [1, 3]) ➞ {(2, 3)}
fair_swap([2, 3, 4], [11, 4, 1]) ➞ set()
```
|
algorithms
|
def fair_swap(a, b):
r = set()
swap_size, odd_diff = divmod(sum(a) - sum(b), 2)
if odd_diff:
return r
b = set(b)
for n1 in set(a):
if (n2 := n1 - swap_size) in b:
r . add((n1, n2))
return r
|
Fair Swap between Two Lists
|
64b7bcfb0ca7392eca9f8e47
|
[
"Algorithms",
"Lists"
] |
https://www.codewars.com/kata/64b7bcfb0ca7392eca9f8e47
|
7 kyu
|
Some idle games use following notation to represent big numbers:
|Number|Notation|Description|
|-|-|-|
|1|1|1|
|1 000|1K|Thousand|
|1 000 000|1M|Million|
|1 000 000 000|1B|Billion|
|1 000 000 000 000|1T|Trillion|
|1 000 000 000 000 000|1aa|Quadrillion|
|10¹⁸|1ab|Quintillion|
|10²¹|1ac|Sextillion|
|10²⁴|1ad|Octillion|
And so on, from `aa` to `az`, then from `ba` to `bz`, etc, until `zz`. The letters before and including trillion should be uppercase, letters after quadrillion should be lowercase to easy distinguish between the 'common' notation and 'aa' one.
## Your task
Your task is to write a function that accepts a floating point number and formats it using the notation given above.
The resulting number should include 3 most significant digits and be rounded down towards zero (for example, `1238` should be `1.23K`, and `-1238` should be `-1.23K`). All trailing zeroes after the decimal point should be removed, and the decimal point should be excluded if the resulting number is whole number of units after the rounding down. If the number is too small and it's rounded down to `0`, then `0` should be returned. Beware of the negative zero, which should not appear in the output, insted the regular zero `0` should be returned.
## Input limitation
The input is a finite floating point number in range `-10³⁰³ < x < 10³⁰³`.
## Examples
```
0 => 0
1 => 1
-1 => -1
123 => 123
0.25 => 0.25
-0.9999 => -0.99
0.009 => 0 (too small)
1000 => 1K
1234 => 1.23K
-4002 => -4K
5809 => 5.8K
100 000 => 100K
123 456 789 => 123M
1 234 567 890 => 1.23B
1 234 567 890 000 => 1.23T
999 999 999 999 999 => 999T
1 234 567 890 000 000 000 => 1.23ab
-0.0000001 => 0
10³⁰⁰ => 1dr
```
## Alphabet for quick copypaste
```abcdefghijklmnopqrstuvwxyz```
|
reference
|
from decimal import Context, Decimal, ROUND_DOWN
from re import sub
def format_number(x):
dec = (
(Context(prec=3, rounding=ROUND_DOWN)
. create_decimal_from_float(x * 100)
. to_integral_exact(rounding=ROUND_DOWN) / 100)
. normalize()
. to_eng_string()
)
return '0' if dec == '-0' else sub(
'E\+(\d+)',
lambda m: ('KMBT' [n - 1] if (n := int(m[1]) / / 3) < 5 else
'' . join(chr(x + 97) for x in divmod(n - 5, 26))),
dec,
)
|
The "AA" Number Notation
|
64e4cdd7f2bfcd142a880011
|
[
"Mathematics"
] |
https://www.codewars.com/kata/64e4cdd7f2bfcd142a880011
|
5 kyu
|
### Spark plugs, distributor wires, and firing order.
Your car's engine operates by containing tiny explosions caused by gas being ignited by spark plugs, which compresses a pistion, causing the engine to turn. Spark plugs are sparked by receiving electrical signal through a wire connected to a distributing system. If you're curious, [here's an explanation of the whole process](https://www.youtube.com/watch?v=ss0GMKBYCks). *If you watch the video, you can ignore the formulas, as this kata is about firing order, and not combustion physics*.
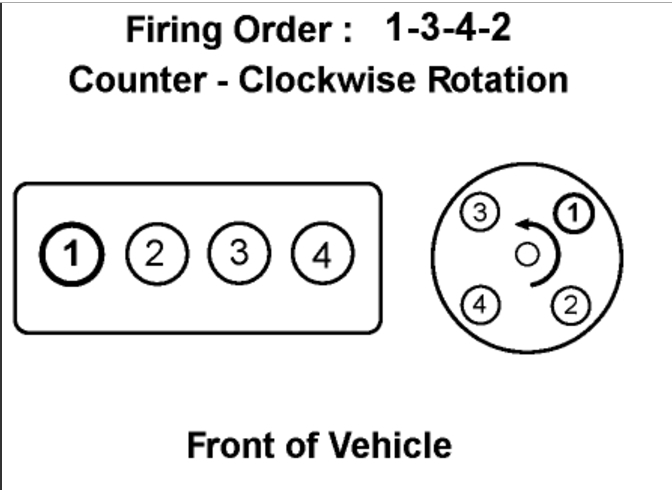
In short, to make sure that this process is balanced, and engine rotation is maintained constantly, **each cylinder of an engine is fired in an order determined by the manufacturer**. There are a few cases where optimal order is very well documented. For example, with an inline 4-cylinder engine, `'I4'` the optimal firing order is `1-3-4-2`. Because of this, most *(but not all...)* manufacturers use this order. With different engine layouts, and sizes, sometimes manufacturers will change the order slightly to give more power but less balance, or less power and more engine longevity.
**Please note: This is not car repair advice. If you think your car has a misfire, please look up the exact engine your car uses before attempting any of these sequences. AKA have fun, trust the mechanic instead of random internet man.**
### Your task is relatively simple
Write a function helps us diagnose where a misfire is located. A misfire is typically caused by a faulty wire, or old spark plug. This causes the engine to fire on every cylinder except the one that is bad. For example, with our typical inline 4 engine, if cylinder #3 has a misfire, the engine would receive full rotation in #1, #4, and #2, but #3 would give no rotation at all, causing major issues. For our case, we are assuming that an engine needs at least 1 cylinder functioning for us to diagnose the bad cylinders.
Your function should take one argument, which is a string with the following syntax:
```
MAKE | ENGINE SIZE | CURRENT ORDER
-----+--------------+----------------
Ford | V8 | 1-X-4-2-X-3-X-8
```
An `"X"` indicates a cylinder that has not fired. Your goal is to return a string with the correct cylinder number, in the correct sequence for that make and engine size. In the example above, the correct return value is: `"5-6-7"`. If there are no misfires, return an empty string. You have been provided with a python nested dictionary named `CARS` that you can call as you please. All elements of `CARS` are strings. The maker is the first key, the engine size is the second key. Below examples that will be included in the test cases.
`INPUT: 'Ford V8 1-X-4-2-X-3-X-8'` | `OUTPUT: '5-6-7'`
`INPUT: 'Cadillac V6 1-2-3-4-5-6'` | `OUTPUT: ''`
`INPUT: 'GMC I4 1-X-4-2'` | `OUTPUT: '3'`
`INPUT: 'Dodge V10 1-X-X-4-3-6-5-X-X-2'` | `OUTPUT: '10-9-8-7'`
|
reference
|
CARS = {
enterprise: {model: ignition . split('-')
for model, ignition in models . items()}
for enterprise, models in CARS . items()
}
def find_misfire(fire_in_the_holes):
enterprise, model, fire = fire_in_the_holes . split()
return '-' . join(a for a, b in zip(CARS[enterprise][model], fire . split('-')) if a != b)
|
Car Debugging: Misfire
|
64dbfcbcf9ab18004d15d17e
|
[
"Strings",
"Fundamentals"
] |
https://www.codewars.com/kata/64dbfcbcf9ab18004d15d17e
|
7 kyu
|
# Task
Your goal is to know the score of the hand, either by getting three cards of the same rank or the same suit. The value of your hand is calculated by adding up the total of your cards in **any one suit**.
Regular cards are worth their number, face cards are worth 10, and Aces are worth 11, but remember, **only one of your suits counts**!
You can also make a hand of **three cards with the same rank**, like 8-8-8 or J-J-J. This is worth 30.5 points unless it is A-A-A, which is worth 32.
Take three strings: **c1, c2, and c3** and return a number **score**.
### Examples
```python
score31("CA", "D9", "H8") ➞ 11
# CA = 11
# D9 = 9
# H8 = 8
# Return max score = 11
score31("SJ", "SQ", "S8") ➞ 28
# SJ + SQ + S8 = 10 + 10 + 8 = 28
score31("DA", "DK", "DQ") ➞ 31
# DA + DK + DQ = 11 + 10 + 10 = 31
score31("S9", "C9", "H9") ➞ 30.5
# Same numbers = 30.5
score31("SA", "CA", "HA") ➞ 32
# All A's = 32
```
### Notes
- Cards are of these suits: `H-hearts, C-clubs, S-spades, and D-diamonds`
- Numbers are: `2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A`
|
algorithms
|
from collections import defaultdict
def score31(c1, c2, c3):
d = defaultdict(int)
values = set()
for c in c1, c2, c3:
v = c[1:]
values . add(v)
d[c[0]] += int(v) if v . isdigit() else 10 + (v == "A")
return max(d . values()) if len(values) > 1 else 30.5 + 1.5 * (v == "A")
|
Card Game 31 Score Validator
|
64e06b8f55bbb752ac2e66f5
|
[] |
https://www.codewars.com/kata/64e06b8f55bbb752ac2e66f5
|
7 kyu
|
*How many squares can Chuck Norris cover in a single jump? All of them!*
A grasshopper is jumping forward in a single-axis space represented as an array(list). It can cover `p` spaces in one jump, where `p` is any prime number.
The grasshopper starts any distance *before* the initial item of the array and finishes any distance *after* the final item of the array. The grasshopper never jumps backwards.
Calculate the **maximum sum** of values of array items the grasshopper can land on while travelling. Since there is no such thing as maximum prime number, it's entirely possible that the grasshopper won't land on any item at all and cover all the distance from start to finish in a single jump.
The array consists of up to 5 000 items ranging from -100 to +100, so make sure your algorithm is fast enough.
For your convenience, prime numbers up to 5003 are preloaded as `PRIMES`.
Examples:
```
[-10, 3, 4, 5, 6] => 10:
/\____\/
,_/ \O0o;;
[-10, 3, 4, 5, 6]
start - skip - skip - land - skip - land - skip - finish
4 + 6 == 10
Grasshopper jumps:
- on distance 3 from start to 4
- on distance 2 from 4 to 6
- on distance 2 from 6 to finish
```
```
[8, 2, 0, -2, -3, -2, -3, -1, 9] => 15:
/\____\/
,_/ \O0o;;
[8, 2, 0, -2, -3, -2, -3, -1, 9]
start - skip - land - skip - land - skip - skip - land - skip - skip - land - skip - finish
8 + 0 - 2 + 9 = 15
Grasshopper jumps:
- on distance 2 from start to 8
- on distance 2 from 8 to 0
- on distance 3 from 0 to -2
- on distabce 3 from -2 to 9
- on distance 2 from 9 to finish
```
```
[-2, -3, -2, -3] => 0:
/\____\/
,_/ \O0o;;
[-2, -3, -2, -3]
start - skip - skip - skip - skip - finish
Grasshopper jumps:
- on distance 5 from start to finish
```
|
algorithms
|
from preloaded import PRIMES
from itertools import chain, takewhile
def prime_grasshopper(arr):
dp = arr[:]
for i, x in enumerate(dp):
dp[i] = max(
chain([x], [dp[i - p] + x for p in takewhile(i . __ge__, PRIMES)]))
return max(chain([0], dp))
|
Prime Grasshopper
|
648b579a731d7526828173cc
|
[
"Dynamic Programming"
] |
https://www.codewars.com/kata/648b579a731d7526828173cc
|
5 kyu
|
## This Kata is the second of three katas that I'm making on the game of hearts. We're getting started by simply scoring a hand, and working our way up to scoring a whole game!
[Link for Kata #1](https://www.codewars.com/kata/64d16a4d8a9c272bb4f3316c)
Now that we can sucessfully score a single hand, we're ready to score a whole round. For a quick example of the rules for hearts, [follow this link](https://gamerules.com/rules/hearts-card-game/).
- Your goal is to take the hand of each of the four players as input, and return a list of winning cards in the order that they were played. You will be given various hand sizes to test with, the minimum size being 2, the maximum being 13. The actual test cases will be 50 random dealings of 13 cards.
#### For the sake of these kata, we are playing a traditional four player game of hearts with some important modifications as follows:
- We are ignoring the rule about playing a ```point card``` in the first hand. This rule is for the sake of player strategy, and implementing it here will only add an extra "if" condition that isn't really in the spirit of this kata. **TO CLARIFY: This means that as long as the player cannot match the suit, they are allowed to play any card on that turn**.
- We are not 'passing' cards. In other words, the cards players recieve are final. They should never recieve extra cards, and the order that a player recieves their cards initially, **should not change**. It does not neccesarily matter if Alex always plays first, (there are circumstances when he will not play first) but the inital order of his cards is essential to the way player logic is written.
- The Queen of Spades ```"QS"``` and any heart card ```"_H"``` are normally considered ```point cards```. There are usually special cases to when you can play a ```point card```, and we are ignoring those rules. For this kata, a player will prioritize playing a heart, or the queen of spades when able.
- Our players are dumb. To work out a valid winning strategy for Hearts is far beyond the scope of this kata series. The player strategy has been explained to you in detail to you for this reason. (See below) Keep in mind, you will have to use this strategy for each player for each turn of the round.
#### Some key rules that we ARE using:
- The "two of clubs" ```"2C"``` card should be the first card played whenever it is in any player's starting hand. If the two of clubs is not present in any of the player's starting hands, the first card played will instead be index 0 of Alex.
- Whoever "wins" a hand will set the starting "suit" for the next hand (This is called the suit being "led"). As an example, the players hands are: ```['2C', '3C']``` | ```['AH', 'KH']``` | ```['2S', 'KC']``` | ```['2D', '3D']``` The first hand would be ```['2C', 'AH', 'KC' '2D']``` Which would result in Chris winning with the king of clubs ```'KC'``` Since Chris won that hand, he gets to lead the next hand, which would be ```['2S', '3D', '3C', 'KH']```. Since no one else played a spade, and Chris set the suit to be spades, he wins this hand with the two of spades ```'2S'```
- If you have not trained in the first kata of the series, here is a refresher of how cards are evaluated. The player who goes first sets the starting suit (as seen in the example above). Every other player **MUST** play a card of the same suit if they have one in their hand. They are exempt from this rule if they do not have any cards with a matching suit. after all cards are played, the "suited" cards are considered, and the highest value card of the suit wins. **Card values are:** ```2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | J | K | Q | A``` **Card suits are:** ```S | H | C | D``` You will need to implement logic that checks this for a successful code, but you will not be directly tested on this. Please try out the first kata if you're having trouble testing any code for determining the winning card of a hand.
## A description of player strategy:
### PLAYERS GOING FIRST
A player is decided to go first by either *winning the previous hand* **or** *they hold the ```"2C"``` card*. If neither of these conditions are met, Alex will play first. If this player does not have the ```"2C"``` card, they will simply play the first card in their hand. This type of card selecting only applies to when a player has won the previous hand, or the existance of the ```"2C"``` has been found.
### PLAYERS WHO ARE NOT GOING FIRST
Player logic has been written as follows. There is a function that takes two positional arguments. The first argument is a list representing the player's hand. The second argument is a string representing the current suit, as described by the other rules. The logic you implement should follow this description as closely as possible to make sure your code passes all tests.
**FIRST CHECK**
- The first thing that this function checks, is for the existence of the two of clubs ```"2C"```. Following the rules means playing this card first if it is in any of the player's hands. If the player has this card in their hands, it is returned on the first line. (This check is left for other players to ensure that the ```"2C"``` is played on the first turn).
**SECOND CHECK**
- The next thing this function checks, is if the player has a card matching the same suit provided to the function. In other words, if the two of clubs is played by Alex, this function will return the first instance of a club suited card in Bob's hand. If a player has a card that matches the suit parameter, they must play that card.
**THIRD CHECK**
- Right now, we know that the player's hand does not have the suited cards. The rules say that we are allowed to play any card we want. **This is a key part of the player logic** To keep things simple, we have two conditions describing this scenario. In this first condition, we will check for any ```point card``` in the players hand. This is any heart card, or the queen of spades. **If a player has any heart, or the queen of spades, they must play it at this point**.
**FINAL CHECK**
- If all of these checks came back with a "False" value, then the player will simply play the first card of his hand. (Index 0, if you have been removing cards from the hand after they are played. Otherwise, this can be described as the first **unseen** card.
**SUMMARY**
```Check for "2C" | Check for suit | Check for point cards | Play the first card in hand```
### EXAMPLES
#### For these examples, they will all be given in order of players. Whoever plays first will be indicated, but the list will follow the format [ALEX, BOB, CHRIS, DAVE]
- Input: ```Alex: ['2C', '3S']``` | ```Bob: ['AH', 'KH']``` | ```Chris: ['AS', 'KS']``` | ```Dave: ['AD', 'KD']```
> Hand one: ```['2C', 'AH', 'KS' 'AD']``` Since Alex was the first player, and no one else played in suit, Alex wins this hand with ```'2C'```
> Hand two: ```['3S', 'KH', 'KS', 'KD']``` Alex led with the 3 of spades. Since Chris played the highest value spade card, he wins this hand with ```'KS'```
This is the end of the round, so final output is ```['2C', 'KS']```
- Input: ```Alex: ['AH', 'KH', 'QH', 'JH']``` | ```Bob: ['2C', '3C', '4C', '5C']``` | ```Chris: ['AS', 'KS', 'QS', 'JS']``` | ```Dave: ['AD', 'KD', 'QD', 'JD']```
> Hand one: ```['AH', '2C', 'AS', 'AD']``` Bob had the two of clubs, and goes first. Since Bob was the only one to play in suit, he wins the hand with ```'2C'``` Bob will also win the rest of the round since he only has clubs, and no one else has clubs. The rest of the round goes like this:
> - ```['KH', '3C', 'KS', 'KD'] -> ['3C']```
> - ```['QH', '4C', 'QS' 'QD'] -> ['4C']```
> - ```['JH', '5C', 'JS', 'JD'] -> ['5C']```
>
> The final output should be: ```['2C', '3C', '4C', '5C']```
- Input: ```Alex: ['2C', '2D', '3D', '4D']``` | ```Bob: ['5D', '6D', '7S', '8S']``` | ```Chris: ['2H', '3H', '10H', '9S']``` | ```Dave: ['4H', '5H', '6H', 'JH']```
> - Hand one: ```['2C', '5D', '2H', '4H']``` Alex has the two of clubs, and plays first. No one else plays in suit, so Alex wins with ```'2C'```
> - Hand two: ```['2D', '6D', '3H', '5H']``` Alex led with diamonds, but Bob played a higher value diamond. Bob wins this hand with ```'6D'```
> - Hand three: ```['3D', '7S', '9S', '6H']``` Bob led with spades, but Chris played a higher value spade. Chris wins this hand with ```'9S'```
> - Hand four: ```['4D', '8S', '10H', 'JH']``` Chris led with hearts, but Dave played a higher value heart. Dave wins with ```'JH'```
> - Final output should be: ``` ['2C', '6D', '9S', 'JH']```
|
games
|
def play_a_round(alex_cards, bob_cards, chris_cards, dave_cards):
return_list = []
if '2C' in bob_cards:
leader = 'bob'
elif '2C' in chris_cards:
leader = 'chris'
elif '2C' in dave_cards:
leader = 'dave'
else:
leader = 'alex'
# Play until players have no more cards
while len(alex_cards) > 0:
# Build this hand
this_hand = []
if leader == 'alex':
this_hand . append(get_card(alex_cards, this_hand))
this_hand . append(get_card(bob_cards, this_hand))
this_hand . append(get_card(chris_cards, this_hand))
this_hand . append(get_card(dave_cards, this_hand))
elif leader == 'bob':
this_hand . append(get_card(bob_cards, this_hand))
this_hand . append(get_card(alex_cards, this_hand))
this_hand . append(get_card(chris_cards, this_hand))
this_hand . append(get_card(dave_cards, this_hand))
elif leader == 'chris':
this_hand . append(get_card(chris_cards, this_hand))
this_hand . append(get_card(alex_cards, this_hand))
this_hand . append(get_card(bob_cards, this_hand))
this_hand . append(get_card(dave_cards, this_hand))
elif leader == 'dave':
this_hand . append(get_card(dave_cards, this_hand))
this_hand . append(get_card(alex_cards, this_hand))
this_hand . append(get_card(bob_cards, this_hand))
this_hand . append(get_card(chris_cards, this_hand))
# Determine winner and add it to list to be returned
winning_card = play_a_hand(this_hand)
return_list . append(winning_card)
# Determine who leads next hand
if winning_card in alex_cards:
leader = 'alex'
elif winning_card in bob_cards:
leader = 'bob'
elif winning_card in chris_cards:
leader = 'chris'
elif winning_card in dave_cards:
leader = 'dave'
# Remove cards just played from players' hands
for card in this_hand:
if card in alex_cards:
alex_cards . remove(card)
elif card in bob_cards:
bob_cards . remove(card)
elif card in chris_cards:
chris_cards . remove(card)
elif card in dave_cards:
dave_cards . remove(card)
return return_list
# Use the strategy from the instructions to determine which card this player plays
def get_card(player_cards, this_hand):
# First check
if '2C' in player_cards:
return '2C'
# Second check
if len(this_hand) == 0:
return player_cards[0]
else:
led_suit = this_hand[0][- 1]
for card in player_cards:
if card[- 1] == led_suit:
return card
# Third check
for card in player_cards:
suit = card[- 1]
if card == 'QS' or suit == 'H':
return card
# Final check
return player_cards[0]
# Which card wins this hand? Return it.
def play_a_hand(cards):
ranks = ['2', '3', '4', '5', '6', '7', '8', '9', '10', 'J', 'Q', 'K', 'A']
suit = cards[0][- 1]
top_rank = cards[0][0: - 1]
for i in range(1, 4):
this_card = cards[i]
this_suit = this_card[- 1]
if this_suit == suit:
this_rank = this_card[0: - 1]
if ranks . index(this_rank) > ranks . index(top_rank):
top_rank = this_rank
return top_rank + suit
|
Hearts (Card Game) Kata 2 of 3
|
64d1d067e58c0e0025860f4b
|
[
"Puzzles",
"Games"
] |
https://www.codewars.com/kata/64d1d067e58c0e0025860f4b
|
5 kyu
|
## AST Series:<br>
+ [Your first use of ast: Inspecting Python Functions](https://www.codewars.com/kata/64d129a576bd58000f7fe97a)
+ AST Series #2: Your First NodeTransformer (this one!)
+ [AST Series #3: The Missing Link](https://www.codewars.com/kata/64dd031d9a9b8c1bc6972e9f)
# Preamble
Today you will learn how to use [NodeTransformer](https://docs.python.org/3/library/ast.html#ast.NodeTransformer).
# Task
You are given a function `manipulate_me` with a single instruction, `return 2 + 2`. Your goal is to use NodeTransformer to manipulate the function to return the value `5`. There are many ways to do this, and I am excited to see what you all come up with.
# Note:
You are only required to modify the behavior of a single BinOp node; other node types should remain unchanged.
# Helpful links:
https://docs.python.org/3/library/ast.html#ast.BinOp<br>
https://docs.python.org/3/library/ast.html#ast.Constant
|
reference
|
import ast
class YourFirstNodeTransformer (ast . NodeTransformer):
... # you can do this !
def visit_Constant(self, node):
return ast . Constant(node . value + 0.5)
|
AST Series #2: Your First NodeTransformer
|
64dbb4ab529cad81578c61e7
|
[] |
https://www.codewars.com/kata/64dbb4ab529cad81578c61e7
|
6 kyu
|
# Task
Given a string of digits, return the longest substring with alternating `odd/even` or `even/odd digits`. If two or more substrings have the same length, return the substring that occurs first.
# Examples
```python
longest_substring("225424272163254474441338664823") ➞ "272163254"
# substrings = 254, 272163254, 474, 41, 38, 23
longest_substring("594127169973391692147228678476") ➞ "16921472"
# substrings = 94127, 169, 16921472, 678, 476
longest_substring("721449827599186159274227324466") ➞ "7214"
# substrings = 7214, 498, 27, 18, 61, 9274, 27, 32
# 7214 and 9274 have same length, but 7214 occurs first.
longest_substring("20") ➞ "2"
longest_substring("") ➞ ""
```
# Input Constraints
- 0 <= len(digits) <= 10^5
|
algorithms
|
import re
def longest_substring(digits):
regex = r'({e}?({o}{e})*{o}?)|({o}?({e}{o})*{e}?)' . format(
e='[02468]', o='[13579]')
return max((x[0] for x in re . findall(regex, digits)), key=len)
|
Longest Alternating Substring
|
64db008b529cad38938c6e28
|
[
"Algorithms",
"Logic",
"Regular Expressions",
"Strings"
] |
https://www.codewars.com/kata/64db008b529cad38938c6e28
|
6 kyu
|
<html>
<body>
Given two sets of integer numbers (domain and codomain), and a list of relationships (x, y) also integers, determine if they represent a function and its type:<br>
<strong>1. Not a function:</strong>
If there is at least one element in the domain set that is related to more than one element in the codomain set.
<br><i>Example:</i>
```python
domain = {10, 20, 30, 40, 50}
codomain = {20, 30, 40, 50}
relations = {(10, 20),(10, 50),(20, 30),(30, 40),(40, 50),(50, 20)}
output = "It is not a function"
```
<i>(this is because the element 10 in the domain is related to more than one element in the codomain, <br>therefore, it does not fulfill the uniqueness criterion).</i><br>
<strong>2. Function:</strong>
Each and every element in the domain set is related to an element in the codomain set.
They are classified as:<br>
<strong>A. Injective:</strong> Every element in the codomain set is related to at most one element in the domain set. In other words, there are no two distinct elements in the domain set that have the same image in the codomain set.<br>
<i>Example:</i>
```python
domain = {1, 2}
codomain = {20, 30, 40}
relations = {(1, 20),(2, 30)}
output = "Injective"
```
<i>(because each element in the codomain is related to zero or at most one element in the domain).</i><br>
<strong>B. Surjective:</strong> All elements in the codomain set are related to at least one element in the domain set. In other words, there are no elements in the codomain set that do not have a preimage in the domain set.<br>
<i>Example:</i>
```python
domain = {1, 2, 3, 4, 5}
codomain = {20, 30, 40, 50}
relations = {(1, 20),(2, 30),(3, 40),(4, 50),(5, 40)}
output = "Surjective"
```
<i>(because all elements in the codomain are related to at least one element in the domain, <br>element 40 has more than one relation in the domain).</i><br>
<strong>C. Bijective:</strong> Every element in the domain set is related to a unique element in the codomain set, and vice versa. Each element in the codomain set has a unique preimage in the domain set, and each element in the domain set has a unique image in the codomain set.<br>
<strong>In other words, a function is bijective when it is injective and surjective at the same time. </strong>
<br><i>Example:</i>
```python
domain = {2, 3, 4}
codomain = {2, 3, 4}
relations = {(3, 4),(2, 3),(4, 2)}
output = "Bijective"
```
<i>(because each element in the codomain is related to exactly one element in the domain).</i><br>
<strong>D. General:</strong> There are elements in the domain set that are related to at least one element in the codomain set, but there may be elements in the codomain set that are not related to any element in the domain set.<br>
<i>Example:</i>
```python
domain = {1, 2, 3}
codomain = {2, 3, 4}
relations = {(1, 4),(2, 4),(3, 4)}
output = "General function"
```
<i>(all elements in the domain are related to at least one element in the codomain,<br> although some elements in the codomain are not related to any element in the domain).</i><br>
<strong>Note: All the first elements in the relations belong to the domain set, and all the second elements belong to the codomain set. </strong>
</body>
</html>
|
reference
|
def type_of_function(d, c, r): return 'It is not a function' if len(k: = dict(r)) != len(r) else ('Bijective' if len(k) == len(d) == len(c) else 'Surjective') if set(k . values()) == set(c) else 'Injective' if len(set(k . values())) == len(k . values()) else 'General function'
|
Type Of Relation
|
64915dc9d40f96004319379a
|
[
"Mathematics",
"Set Theory"
] |
https://www.codewars.com/kata/64915dc9d40f96004319379a
|
7 kyu
|
<details open>
<summary style="
padding: 3px;
width: 100%;
border: none;
font-size: 18px;
box-shadow: 1px 1px 2px #bbbbbb;
cursor: pointer;">
Task</summary>
> Given positive integer <code>n</code> return an array of array of numbers, with the nested arrays representing all possible ways to make groups of sizes that are a multiple of <code>2</code>of items in any source array of size <code>n</code> and the numbers representing the indices of the items.
- This is a subset of a more generalised, harder problem, with tighter performance constraints: <a href="https://www.codewars.com/kata/64d7d0b6529cad8b528c7546">Polygroup Mania</a>
</details>
<details open>
<summary style="
padding: 3px;
width: 100%;
border: none;
font-size: 18px;
box-shadow: 1px 1px 2px #bbbbbb;
cursor: pointer;">
Specification</summary>
Constraints:
- Output can grow huge, so range of <code>n</code> is <code>0 - K</code> (upper limit included).
- Javascript: <code>K = 21</code>
- Python: <code>K = 20</code>
- There are medium performance constraints.
- Code length limited to <code>2000</code> characters to prevent hardcoding.
Rules:
- Groups contain combinations (not permutations) of element indices
- Element indices within each group should be ascending, gaps are allowed, duplicates are not
- The sizes of the groups must be multiples of <code>2</code> that fit <code>n</code>; in order to fit <code>multiplier * 2 ≤ n</code>
- Empty groups are not eligible and should be discarted
- Groups are sorted by value of index, ascending; on tie, by value of next index and so on ... still a tie: on length of group descending
Examples:
```
input: pairEmUp(2)
expected result : [ [ 0, 1 ] ]
The group size of multiples of 2 that fit n = 2
is 2.
So the results contain groups of size 2.
```
```
input: pairEmUp(3)
expected result : [ [ 0, 1 ], [ 0, 2 ], [ 1, 2 ] ]
The group size of multiples of 2 that fit n = 3
is 2.
So the results contain groups of size 2.
```
```
input: pairEmUp(4)
expected result : [ [ 0, 1, 2, 3 ], [ 0, 1 ], [ 0, 2 ], [ 0, 3 ], [ 1, 2 ], [ 1, 3 ], [ 2, 3 ] ]
The group sizes of multiples of 2 that fit n = 4
are 2 and 4.
So the results contain groups of size 2 and 4.
```
```
n expected result
0 []
1 []
2 [ [ 0, 1 ] ]
3 [ [ 0, 1 ], [ 0, 2 ], [ 1, 2 ] ]
4 [ [ 0, 1, 2, 3 ], [ 0, 1 ], [ 0, 2 ], [ 0, 3 ], [ 1, 2 ], [ 1, 3 ], [ 2, 3 ] ]
5 [ [ 0, 1, 2, 3 ], [ 0, 1, 2, 4 ], [ 0, 1, 3, 4 ], [ 0, 1 ], [ 0, 2, 3, 4 ], [ 0, 2 ], [ 0, 3 ], [ 0, 4 ], [ 1, 2, 3, 4 ], [ 1, 2 ], [ 1, 3 ], [ 1, 4 ], [ 2, 3 ], [ 2, 4 ], [ 3, 4 ] ]
```
</details>
Good luck!
|
algorithms
|
from itertools import combinations
def pair_em_up(n):
return sorted((list(x) for k in range(2, n + 1, 2) for x in combinations(range(n), k)), key=lambda x: x + [n] * (n - len(x)))
|
Pair 'em Up
|
64d4cd29ff58f0002301d5db
|
[
"Algorithms",
"Arrays",
"Recursion"
] |
https://www.codewars.com/kata/64d4cd29ff58f0002301d5db
|
5 kyu
|
# Task
Create a function that takes a list of integers and a group length as parameters. Your task is to determine if it's possible to split all the numbers from the list into groups of the specified length, while ensuring that consecutive numbers are present within each group.
# Input
`lst` / `arr`: A list / array of integers representing the numbers to be divided into groups.
`group_len` / `groupLen`: An integer indicating the desired length of each group.
# Output
The function should return `True` if it's possible to create groups according to the criteria, and `False` otherwise.
# Examples
```javascript
consecutiveNums([1, 3, 5], 1) ➞ true
// It is always possible to create groups of length 1.
consecutiveNums([5, 6, 3, 4], 2) ➞ true
// Two groups of length 2: [3, 4], [5, 6]
consecutiveNums([1, 3, 4, 5], 2) ➞ false
// It is possible to make one group of length 2, but not a second one.
consecutiveNums([1, 2, 3, 6, 2, 3, 4, 7, 8], 3) ➞ true
// [1, 2, 3], [2, 3, 4], [6, 7, 8]
consecutiveNums([1, 2, 3, 4, 5], 4) ➞ false
// The list length is not divisible by the group’s length.
```
```python
consecutive_nums([1, 3, 5], 1) ➞ True
# It is always possible to create groups of length 1.
consecutive_nums([5, 6, 3, 4], 2) ➞ True
# Two groups of length 2: [3, 4], [5, 6]
consecutive_nums([1, 3, 4, 5], 2) ➞ False
# It is possible to make one group of length 2, but not a second one.
consecutive_nums([1, 2, 3, 6, 2, 3, 4, 7, 8], 3) ➞ True
# [1, 2, 3], [2, 3, 4], [6, 7, 8]
consecutive_nums([1, 2, 3, 4, 5], 4) ➞ False
# The list length is not divisible by the group’s length.
```
# Input Constraints
~~~if:javascript
- 3 <= arr.length <= 10^4
- 1 <= groupLen <= 10
~~~
~~~if:python
- 3 <= len(lst) <= 10^4
- 1 <= group_len <= 10
~~~
~~~if:php
- 3 <= count(arr) <= 10^4
- 1 <= groupLen <= 10
~~~
|
reference
|
from collections import Counter
def consecutive_nums(lst, size):
if len(lst) % size:
return False
cnt = Counter(lst)
for v in sorted(cnt)[: - size + 1 or None]:
if not cnt[v]:
continue
n = cnt[v]
for x in range(v, v + size):
if cnt[x] < n:
return False
cnt[x] -= n
return not sum(cnt . values())
|
Divide and Conquer
|
64d482b76fad180017ecef0a
|
[
"Algorithms",
"Arrays",
"Performance"
] |
https://www.codewars.com/kata/64d482b76fad180017ecef0a
|
6 kyu
|
### Task
Given an initial chess position and a list of valid chess moves starting from that position, compute the final position.
(a) Positions are represented as 2-d lists of characters; uppercase letters denote white pieces and lowercase black. Empty squares are indicated using <code>.</code> (a single period). White moves up the board.
The position on the left below is represented as shown on the right. This starting position is used in the examples below.
```
8 ...qk..r posn = [ ['.', '.', '.', 'q', 'k', '.', '.', 'r'],
7 ..p..p.p ['.', '.', 'p', '.', '.', 'p', '.', 'p'],
6 n....... ['n', '.', '.', '.', '.', '.', '.', '.'],
5 .P..N..b ['.', 'P', '.', '.', 'N', '.', '.', 'b'],
4 .....p.. ['.', '.', '.', '.', '.', 'p', '.', '.'],
3 .....P.. ['.', '.', '.', '.', '.', 'P', '.', '.'],
2 ....P... ['.', '.', '.', '.', 'P', '.', '.', '.'],
1 R...K..Q ['R', '.', '.', '.', 'K', '.', '.', 'Q'] ]
abcdefgh
```
(b) Each move is a string showing the initial square and destination square, with <code>-</code> between them denoting a non-capturing move and <code>x</code> a capture. Squares are denoted by horizontal and vertical coordinates - the horizontal coordinate is <code>a to h</code> and the vertical coordinate is <code>1 to 8.</code> For example, in the position above the white knight <code>N</code> stands on <code>e5</code>.
### Example
Given inputs <code>posn, ["h1xh5", "d8-a8", "h5xf7"]</code>, we see that the white queen went from h1 to f7, capturing two black pawns on the way. Meanwhile the black queen moved to the top-left corner. The function should return the following position:
```
[ ['q', '.', '.', '.', 'k', '.', '.', 'r'],
['.', '.', 'p', '.', '.', 'Q', '.', 'p'],
['n', '.', '.', '.', '.', '.', '.', '.'],
['.', 'P', '.', '.', 'N', '.', '.', '.'],
['.', '.', '.', '.', '.', 'p', '.', '.'],
['.', '.', '.', '.', '.', 'P', '.', '.'],
['.', '.', '.', '.', 'P', '.', '.', '.'],
['R', '.', '.', '.', 'K', '.', '.', '.'] ]
```
### Details
How each piece moves is explained at https://en.wikipedia.org/wiki/Rules_of_chess. You don't actually need this, as the function does not have to validate that the moves are legal - it should just execute the moves in order and return the final position that results. And it doesn't need to take check or checkmate into account.
The function should handle castling, pawn-promotion, and en-passant.
(a) Castling (see https://en.wikipedia.org/wiki/Castling)
King-side castling is denoted by <code>O-O</code> (capital letter O's, not zeros) and queen-side castling by <code>O-O-O</code>. To determine which side has castled, we need to know whose move it is. Following standard chess notation, if the first move made in the position is black's move, it is preceded in the move list with <code>...</code> (which represents the unknown move that white made previously). Otherwise, the first move is white's move.
Consider the inputs <code>posn, [..., "O-O", "O-O-O"]</code>. From the <code>...</code> we know that black castled king-side and then white castled queen-side. So the function should return
```
[ ['.', '.', '.', 'q', '.', 'r', 'k', '.'],
['.', '.', 'p', '.', '.', 'p', '.', 'p'],
['n', '.', '.', '.', '.', '.', '.', '.'],
['.', 'P', '.', '.', 'N', '.', '.', 'b'],
['.', '.', '.', '.', '.', 'p', '.', '.'],
['.', '.', '.', '.', '.', 'P', '.', '.'],
['.', '.', '.', '.', 'P', '.', '.', '.'],
['.', '.', 'K', 'R', '.', '.', '.', 'Q'] ]
```
(b) Pawn-promotion (see https://en.wikipedia.org/wiki/Promotion_(chess))
Pawn-promotion is indicated by putting the promoted piece's symbol at the end of the move, e.g. <code>"a7-a8Q"</code>. A pawn can promote to any piece of its own color except a king or pawn. The promotion move may capture an enemy piece.
Example: <code>posn, ["b5xa6", "h5xf3", "a6-a7", "f3xe2", "a7-a8Q", "e2-b5"]</code> should return
```
[ ['Q', '.', '.', 'q', 'k', '.', '.', 'r'],
['.', '.', 'p', '.', '.', 'p', '.', 'p'],
['.', '.', '.', '.', '.', '.', '.', '.'],
['.', 'b', '.', '.', 'N', '.', '.', '.'],
['.', '.', '.', '.', '.', 'p', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', '.'],
['R', '.', '.', '.', 'K', '.', '.', 'Q'] ]
```
(c) En-passant (see https://en.wikipedia.org/wiki/En_passant)
Although pawns usually capture diagonally, in one situation a pawn can capture an enemy pawn on the square horizontally next to it - called "**en-passant**" ("in passing"). This is allowed if on the previous move the enemy pawn moved two squares from its initial position; it can then be captured as if it only moved one square. En-passant is indicated by writing the captured pawn's square as if it was captured in the regular way and then putting <code>ep</code> at the end of the move.
Example: <code>posn, ["...", "c7-c5", "b5xc6ep", "d8-c7", "e2-e4", "f4xe3ep"]</code> should return
```
[ ['.', '.', '.', '.', 'k', '.', '.', 'r'],
['.', '.', 'q', '.', '.', 'p', '.', 'p'],
['n', '.', 'P', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', 'N', '.', '.', 'b'],
['.', '.', '.', '.', '.', '.', '.', '.'],
['.', '.', '.', '.', 'p', 'P', '.', '.'],
['.', '.', '.', '.', '.', '.', '.', '.'],
['R', '.', '.', '.', 'K', '.', '.', 'Q'] ]
```
|
reference
|
def compute_final_position(b, m):
def pos(a, b): return (8 - int(b), 'abcdefgh' . index(a))
for t, e in enumerate(m):
if e[2] in '-x':
i, j = pos(* e[0: 2])
p, q = pos(* e[3: 5])
b[p][q] = b[i][j]
b[i][j] = '.' # regular move
if e[- 2:] == 'ep':
b[i][q] = '.' # en passant
if len(e) == 6:
b[p][q] = e[5] # pawn promotion
if e == 'O-O' and t % 2 < 1:
b[7][4] = b[7][7] = '.'
b[7][5] = 'R'
b[7][6] = 'K' # castling king size white
if e == 'O-O' and t % 2 > 0:
b[0][4] = b[0][7] = '.'
b[0][5] = 'r'
b[0][6] = 'k' # castling king size black
if e == 'O-O-O' and t % 2 < 1:
b[7][0] = b[7][4] = '.'
b[7][2] = 'K'
b[7][3] = 'R' # castling queen size white
if e == 'O-O-O' and t % 2 > 0:
b[0][0] = b[0][4] = '.'
b[0][2] = 'k'
b[0][3] = 'r' # castling queen size black
return b
|
Find the Final Position
|
64cd52397a14d81a9f78ad3e
|
[
"Games"
] |
https://www.codewars.com/kata/64cd52397a14d81a9f78ad3e
|
6 kyu
|
## This Kata is the first of three katas that I'm making on the game of hearts. We're getting started by simply scoring a hand, and working our way up to scoring a whole game!
In this Kata, your goal is to evaluate a single hand of hearts, and determine the winning card. Follow this link (https://gamerules.com/rules/hearts-card-game/) for more in depth rules, but the basic rules are as follows.
> There are no "trump" cards in hearts. This means that the first card played will always
> win the hand if it is the only card of that suit.
>
>> EG: If Alex plays the two of clubs ```"2C"``` Bob plays the three of spades ```"3S"``` Chris plays
>> the king of diamonds ```"KD"``` and Dave plays the two of hearts ```"2H"``` **Alex wins that hand**.
>
> Card values are 2 as the lowest card and Ace as the highest card, following typical
> deck of cards order. There will be no duplicate cards given.
>
> The return value of this function should be the winning card as a string, ***Case Sensitive***
>
> For the sake of this Kata, there are no other major rules that need to be followed. In
> other words, it does not matter if this is the first hand, or the last hand. All that
> matters is the value of the highest card in regard to the other rules. This is only for
> a 4-player game of hearts. No need for testing more or less players.
Here are a few examples of what a sucessful code would do. See other test cases for more in depth tests. A set of 50 random tests will be used before you can submit.
> The hand played (input) : ```['10C', 'JC','AC', 'QC']``` Everyone played in suit, so the
> highest card in this set wins. Output should be: ```'AC'```
>
> The hand played (input) : ```['4C', 'KH', 'QS', '10D']``` Alex led with clubs. No one else
> played clubs, so Alex wins this hand even though everyone else's card is higher.
> Output should be: ```'4C'```
>
> The hand played (input) : ```['9D', '9C', 'QD', '9S']``` Only Alex and Chris played in suit.
> Of the two cards that are in suit, Chris' card is a higher value. Output should be: ```'QD'```.
|
games
|
VALUES = ['2', '3', '4', '5', '6', '7', '8', '9', '10', 'J', 'Q', 'K', 'A']
def score_a_hand(cards):
suit = cards[0][- 1]
in_suit = filter(lambda card: card . endswith(suit), cards)
return max(in_suit, key=lambda card: VALUES . index(card[: - 1]))
|
Hearts (Card Game) Kata 1 of 3
|
64d16a4d8a9c272bb4f3316c
|
[
"Games",
"Puzzles"
] |
https://www.codewars.com/kata/64d16a4d8a9c272bb4f3316c
|
7 kyu
|
## Task
You are given 3 positive integers `a, b, k`. Using one operation you can change `a` or `b` (but not both) by `k` (add or subtract are all ok). Count the minimum number of operations needed to make `a, b > 0` and `gcd(a, b) > 1`.
You have to write a function `gcd_neq_one()` which receives 3 positive integers `a, b, k` and return a positive integer: the solution of the problem.
## Examples
**Input:** `a=5, b=9, k=1`
**Output:**
Doing a single operation of (+k) to `a` (5 + 1 * 1) results in gcd(6,9) = 3
**Minimum moves required:** 1 operation
**Input:** `a=2, b=3, k=6`
**Output:**
Doing 3 operations of (+k) to `a` (2 + 3 * 6) and 2 operations of (+k) to `b` (3 + 2 * 6) results in gcd(20,15) = 5
**Minimum moves required:** 5 operations
---
You can read the original, Vietnamese statement at my page (TLEoj): https://tleoj.edu.vn/problem/21c
|
algorithms
|
from math import gcd
from itertools import count
def gcd_neq_one(a, b, k):
for n in count(0):
for i in range(0, n * k + 1, k):
for ai in (a + i, a - i):
if ai > 1:
j = n * k - i
for bj in (b + j, b - j):
if bj > 1 and gcd(ai, bj) > 1:
return n
|
GCD not equal to 1
|
64d0f8fc8a9c270041f33a3c
|
[
"Mathematics",
"Number Theory"
] |
https://www.codewars.com/kata/64d0f8fc8a9c270041f33a3c
|
6 kyu
|
### Task
The function is given a list of `prerequisites` needed to complete some jobs. The list contains pairs `(j, i)`, where job `j` can start after job `i` has been completed. A job can have multiple dependencies or have no dependencies at all. If a job has no dependencies, it can be completed immediately. The function checks if all jobs can be finished and returns `True` if they can be completed, or `False` otherwise.
### Examples
```python
prerequisites = [(1, 0)] # True
# job-0 has no dependency and can be finished.
# job-1 depends on job-0, so it can also be finished.
prerequisites = [(1, 0), (0, 1)] # False
# Neither job-0 nor job-1 can be finished because they are mutually dependent.
prerequisites = [(1, 0), (2, 1)] # True
# The jobs are sequentially dependent.
prerequisites = [(0, 1), (1, 2), (2, 0)] # False
# Circular dependence between 0-1-2-0 prevents them from being finished.
prerequisites = [] # True
# No dependence.
```
### Input Constraints
- 0<= len(prerequisites) <=10^5
- Job identifiers will always be numbers, 0<= i,j <=10^5
|
reference
|
from collections import defaultdict, deque
def finish_all(edges):
n_entrants = defaultdict(int)
succs = defaultdict(list)
for b, a in edges:
n_entrants[b] += 1
n_entrants[a] += 0
succs[a]. append(b)
q = deque(k for k, n in n_entrants . items() if not n)
while q:
a = q . popleft()
del n_entrants[a]
for b in succs[a]:
n_entrants[b] -= 1
if not n_entrants[b]:
q . append(b)
return not n_entrants
|
Dependable Jobs Schedule
|
64cf5ba625e2160051ad8b71
|
[] |
https://www.codewars.com/kata/64cf5ba625e2160051ad8b71
|
5 kyu
|
You are given a positive integer n. For every operation, subtract n by the sum of its digits. Count the number of operations to make n = 0.
For example, with n = 20, you have to use 3 operations. Firstly, n = 20 - (2 + 0) = 18. Secondly, n = 18 - (1 + 8) = 9. Finally, n = 9 - 9 = 0.
You have to answer q such questions.
*You can get the original, Vietnamese statement here: https://tleoj.edu.vn/problem/24e*
*Some subtasks in the original problem have been rewritten to be suitable with Python language*
**In this subtask, `q <= 1 000, n <= 7 * 10 ** 6`**
You can solve each subtask in independent katas:
- Subtask 4: [this kata](https://www.codewars.com/kata/64cfc5f033adb608e2aaedef)
- Subtask 6: [this kata](https://www.codewars.com/kata/64cf783d39f59a002a8f128f)
You have to write a function named `jump_to_zero()` which receives an array (of q positive intergers) and returns an array (of q positive intergers).
Example:
- Input: `[18, 19, 20]`
- Output: `[2, 2, 3]`
There are `1101` testcases in the test kit, include:
- Example test (1 test): `[18, 19, 20]`
- Subtask 2 (100 tests): `n <= 10 ** 5`
- Subtask 3 (500 tests): `n <= 10 ** 6`
- Subtask 4 (500 tests): `n <= 7 * 10 ** 6`
From TLEoj team with love <3
|
algorithms
|
memo = [0] * (10 * * 7)
def solve_using_prev(n):
memo[n] = memo[n - sum(int(x) for x in str(n))] + 1
for n in range(1, 8):
solve_using_prev(n)
for n in range(9, 10 * * 7, 9):
solve_using_prev(n)
def jump_to_zero(a): return [memo[x - sum(int(x)
for x in str(x))] + 1 for x in a]
|
Jump to zero (Subtask 4)
|
64cfc5f033adb608e2aaedef
|
[
"Mathematics",
"Algorithms",
"Dynamic Programming",
"Performance",
"Number Theory"
] |
https://www.codewars.com/kata/64cfc5f033adb608e2aaedef
|
5 kyu
|
### Task
You are given a positive integer `n`. Your objective is to transform this number into another number with **all digits identical**, while _minimizing the number of changes_. Each step in the transformation involves incrementing or decrementing a digit by one.
For example, if the given number is **399**, it can be transformed into **999** in 6 steps by incrementing the first digit by 6. Converting to any other identical digits number would take more than 6 steps.
If `n` already consists of identical digits, the function should return `0`, as no changes are needed. Wrapping, which means moving from `9 to 0` or `0 to 9` in one step, is not allowed.
### Examples
```
399 ➞ 6
# 399 transformed to 999 in 6 steps.
1234 ➞ 4
# there are two possible transformations with identical digits: 2222 and 3333.
# The function should return 4 as it takes 4 steps to transform 1234 into either 2222 or 3333.
# The steps involved could be either incrementing or decrementing a digit by one at a time until all digits become the same.
900 ➞ 9
# 900 can be transformed to 000 after decrementing first digit 9 times to `0`.
7777 ➞ 0
```
|
reference
|
def smallest_transform(num):
lst = [int(i) for i in str(num)]
number = []
for i in range(min(lst), max(lst) + 1):
total = 0
for k in lst:
total += abs(k - i)
number . append(total)
return min(number)
|
Smallest Transform
|
64cf34314e8a905162e32ff5
|
[
"Algorithms",
"Mathematics"
] |
https://www.codewars.com/kata/64cf34314e8a905162e32ff5
|
7 kyu
|
Find the sum of all positive integer roots up to (and including) the nth term of n, whose products are rational positive integers.
Simple...
Right?
Examples:
```csharp
function(1) => 1 as (1root 1 = 1);
function(9) => 12 as (1root 9 = 9) + (2root 9 = 3);
function(27) => 30 as (1root 27 = 27) + (3root 27 = 3);
function(64) => 78 as (1root 64 = 64) + (2root 64 = 8) + (3root 64 = 4) + (6root 64 = 2);
```
Test Cases:
1. Five select test cases (which are visible to you).
2. Of the five, the last is the hardest and will test the precision of your floating point values.
3. The first 5000 numbers will be tested.
4. Then 100 randomly generated numbers from 1,000,000 to 10,000,000 will be tested.
5. Finally, the first 30 powers of 2 will be tested.
Tip:
**Be careful of data types and floating point values**
|
algorithms
|
from gmpy2 import iroot
def root_sum(n):
return sum(r[0] for k in range(1, n . bit_length() + 1) if (r := iroot(n, k))[1])
|
Root the Num and Find the Integer Sum
|
64cbc840129300011fa78108
|
[
"Mathematics"
] |
https://www.codewars.com/kata/64cbc840129300011fa78108
|
6 kyu
|
You will be given an array of events, which are represented by strings. The strings are dates in HH:MM:SS format.
It is known that all events are recorded in chronological order and two events can't occur in the same second.
Return the minimum number of days during which the log is written.
Example:
```python
Input -> ["00:00:00", "00:01:11", "02:15:59", "23:59:58", "23:59:59"]
Output -> 1
Input -> ["12:12:12"]
Output -> 1
Input -> ["12:00:00", "23:59:59", "00:00:00"]
Output -> 2
Input -> []
Output -> 0
```
Good luck
|
algorithms
|
def check_logs(log): return sum(
a >= b for a, b in zip(log, log[1:])) + bool(log)
|
Log without dates
|
64cac86333ab6a14f70c6fb6
|
[
"Date Time",
"Filtering"
] |
https://www.codewars.com/kata/64cac86333ab6a14f70c6fb6
|
7 kyu
|
# Task
A courthouse has a backlog of several cases that need to be heard, and is trying to set up an efficient schedule to clear this backlog. You will be given the following inputs:
- A dictionary `cases` whose values are the number of court sessions each case needs to be concluded.
- An integer `max_daily_sessions` which gives the maximum number of court sessions that can be held each day.
Crucially, it is _not possible_ to have two sessions of the same case in the same day.
Write a function that determines the **minimum number of days** needed to clear the backlog.
# Examples
```python
legal_backlog({"A":4, "B": 3, "C": 2}, 5) ➞ 4
# There are three cases "A", "B", "C" needing 4, 3, 2 sessions, respectively.
# Moreover, up to five sessions can be held each day.
# A possible schedule is:
# day1 = ["A", "B", "C"], day2 = ["A", "B", "C"], day3 = ["A", "B"],
# day4 = ["A"]
legal_backlog({"A":4, "B": 3, "C": 2}, 3) ➞ 4
# Same cases as above, but now with up to three sessions each day
# Same schedule as above still words
legal_backlog({"A":4, "B": 3, "C": 2}, 1) ➞ 9
# Again same cases, but only one case per day,
# hence answer is the number of cases, i.e. 9
legal_backlog({"A":4, "B": 3, "C": 2}, 2) ➞ 5
# Same cases, but at most two sessions per day.
# A possible schedule:
# day1 = ["A", "B"], day2 = ["A", "B"], day3 = ["A", "B"],
# day4 = ["A", "C"], day5 = ["C"]
legal_backlog({"A":4, "B": 4, "C": 4}, 2) ➞ 6
# Different case load, at most two sessions per day
# A possible schedule:
# day1 = ["A", "C"], day2 = ["A", "C"], day3 = ["A", "B"],
# day4 = ["A", "B"], day5 = ["C", "B"], day6 = ["C", "B"]
```
# Inpurt Constraints
- Easy - 30 test cases with 1<=len(cases)<5
- Medium - 20 test cases with 5<=len(cases)<15
- Hard - 20 test cases with 15<=len(cases)<=25
|
algorithms
|
from math import ceil
def legal_backlog(cases, mds):
return max(ceil(sum(cases . values()) / mds), max(cases . values()))
|
Legal Backlog
|
64c64be38f9e4603e472b53a
|
[] |
https://www.codewars.com/kata/64c64be38f9e4603e472b53a
|
6 kyu
|
Write a function `revSub` which reverses all sublists where consecutive elements are even.
Note that the odd numbers should remain where they are.
# Example
With `[1,2,4,5,9]` as input, we should get `[1,4,2,5,9]`.
Here, because `[2,4]` is a sublist of consecutive even numbers, it should be flipped. There could be more than one sublist of even numbers, or none at all.
A few other examples:
- `[] -> []`
- `[2,4] -> [4,2]`
- `[2,4,3] -> [4,2,3]`
- `[2,4,3,10,2] -> [4,2,3,2,10]`
Have fun coding!
|
reference
|
from itertools import groupby
def rev_sub(arr):
r = []
for i in [list(g) for n, g in groupby(arr, key=lambda x: x % 2)]:
if i[0] % 2:
r += i
else:
r += i[:: - 1]
return r
|
Reverse sublists of even numbers
|
64c7bbad0a2a00198657013d
|
[
"Lists"
] |
https://www.codewars.com/kata/64c7bbad0a2a00198657013d
|
7 kyu
|
# Task
Create a class that imitates a select screen. The cursor can move to left or right!
In the display method, return a string representation of the list, but with square brackets around the currently selected element. Also, create the methods `to_the_right` and `to_the_left` which moves the cursor.
The cursor should start at index 0.
# Examples
```
menu = Menu([1, 2, 3])
menu.display() ➞ "[[1], 2, 3]"
menu.to_the_right()
menu.display() ➞ "[1, [2], 3]"
menu.to_the_right()
menu.display() ➞ "[1, 2, [3]]"
menu.to_the_right()
menu.display() ➞ "[[1], 2, 3]"
menu.to_the_left()
menu.display() ➞ "[1, 2, [3]]"
menu.to_the_left()
menu.display() ➞ "[1, [2], 3]"
```
# Notes
The cursor should wrap back round to the start once it reaches the end.
|
reference
|
class Menu:
def __init__(self, menu: list) - > None:
self . menu = menu
self . index = 0
self . length = len(menu)
def to_the_right(self) - > None:
self . index = (self . index + 1) % self . length
def to_the_left(self) - > None:
self . index = (self . index - 1) % self . length
def display(self) - > str:
temp = self . menu . copy()
temp[self . index] = [self . menu[self . index]]
return str(temp)
|
Menu Display
|
64c766dd16982000173d5ba1
|
[
"Fundamentals",
"Object-oriented Programming"
] |
https://www.codewars.com/kata/64c766dd16982000173d5ba1
|
7 kyu
|
Given a 2D array of some suspended blocks (represented as hastags), return another 2D array which shows the *end result* once gravity is switched on.
### Examples
```
switch_gravity([
["-", "#", "#", "-"],
["-", "-", "-", "-"],
["-", "-", "-", "-"],
["-", "-", "-", "-"]
]) ➞ [
["-", "-", "-", "-"],
["-", "-", "-", "-"],
["-", "-", "-", "-"],
["-", "#", "#", "-"]
]
switch_gravity([
["-", "#", "#", "-"],
["-", "-", "#", "-"],
["-", "-", "-", "-"],
]) ➞ [
["-", "-", "-", "-"],
["-", "-", "#", "-"],
["-", "#", "#", "-"]
]
switch_gravity([
["-", "#", "#", "#", "#", "-"],
["#", "-", "-", "#", "#", "-"],
["-", "#", "-", "-", "-", "-"],
["-", "-", "-", "-", "-", "-"]
]) ➞ [
["-", "-", "-", "-", "-", "-"],
["-", "-", "-", "-", "-", "-"],
["-", "#", "-", "#", "#", "-"],
["#", "#", "#", "#", "#", "-"]
]
```
### Notes
Each block falls individually, meaning there are no rigid objects. Think about it like falling sand in Minecraft as opposed to the rigid blocks in Tetris.
|
algorithms
|
def switch_gravity(lst):
return list(map(list, zip(* map(sorted, zip(* lst)))))[:: - 1]
|
Switch on the Gravity
|
64c743cb0a2a00002856ff73
|
[
"Algorithms",
"Matrix",
"Arrays"
] |
https://www.codewars.com/kata/64c743cb0a2a00002856ff73
|
7 kyu
|
Given some class `A` with weirdly type-annotated class attributes:
```python
class A:
x: IncrementMe = 5
y: DoubleMe = 21
z: AmIEven = 3
xs: Map(IncrementMe) = [1, 2, 3]
ys: Filter(AmIEven) = [0, 3, 4, 5]
```
and the "magical" function `do_the_magic(kls)` that takes a class (note: the actual class, not an instance of it), after the call of `do_the_magic(A)`, you now have:
```python
print(A.x, A.y, A.z) # 6 42 False
print(A.xs) # [2, 3, 4]
print(A.ys) # [0, 4]
```
So, attributes annotated with:
- `IncrementMe` should be increased by one
- `DoubleMe` should be doubled
- `AmIEven` should be `True` if they are even and `False` otherwise
- `Map(f)` should apply `f` to each element of their array, and `f` can be either one of `IncrementMe`, `DoubleMe`, `AmIEven`, another `Map` or `Filter`, or an actual function like `lambda x: x + 1`
- `Filter(p)` should keep only those array elements that satisfy a predicate `p`, and `p` can be `AmIEven` or an actual function like `lambda x: x > 0`
The annotation itself may also be used as a function directly, i. e. `IncrementMe(41) = 42`, `Map(IncrementMe)([1, 2]) = [2, 3]`, `Filter(lambda _: False)(any_arr) = []`
You have to implement these five "annotations" and the "magical" `do_the_magic(kls)`.
Good luck!
|
games
|
class C:
def __init__(self, fn): self . fn = fn
def __call__(self, * args, * * kwargs): return self . fn(* args, * * kwargs)
IncrementMe = C(lambda v: v + 1)
DoubleMe = C(lambda v: v * 2)
AmIEven = C(lambda v: v % 2 == 0)
def Map(fn): return C(lambda l: list(map(fn, l)))
def Filter(fn): return C(lambda l: list(filter(fn, l)))
def do_the_magic(kls):
for k, p in kls . __annotations__ . items():
if isinstance(p, C):
setattr(kls, k, p(getattr(kls, k)))
|
Using type annotations the wrong way!
|
64c5886e24409ea62aa0773a
|
[
"Puzzles"
] |
https://www.codewars.com/kata/64c5886e24409ea62aa0773a
|
6 kyu
|
Given a string of lowercase letters, find substrings that consist of consecutive letters of the lowercase English alphabet and return a similar string, but with these substrings in reversed alphabetical order.
examples:
("x<font color='red'>abc</font>")=> "x<font color='red'>cba</font>"
xa is not found in the alphabet, but abc is found, so it is reversed.
("<font color='red'>pqrs</font>x<font color='green'>def</font>")=> "<font color='red'>srqp</font>x<font color='green'>fed</font>"
("<font color='red'>jkl</font><font color='green'>xyz</font>")=> "<font color='red'>lkj</font><font color='green'>zyx</font>"
("<font color='red'>vwx</font><font color='green'>cdefg</font>")=> "<font color='red'>xwv</font><font color='green'>gfedc</font>"
("vv<font color='red'>mno</font>zz<font color='green'>stu</font>bb")=> "vv<font color='red'>onm</font>zz<font color='green'>uts</font>bb"
Note: if there are no alphabet substrings in the input string, return the input string as is.
All inputs will consist of one or more lowercase letters. This kata uses only lowercase strings.
|
reference
|
def solution(s):
res, cur = [], [s[0]]
for x in s[1:]:
if ord(x) - ord(cur[- 1]) == 1:
cur . append(x)
else:
res . extend(cur[:: - 1])
cur = [x]
return '' . join(res + cur[:: - 1])
|
Alphabet Slices
|
64c45287edf1bc69fa8286a3
|
[
"Strings",
"Algorithms",
"Fundamentals"
] |
https://www.codewars.com/kata/64c45287edf1bc69fa8286a3
|
6 kyu
|
Your task is to write a function that takes a number as an argument and returns some number. But what's the problem? You need to guess what number should be returned. See the example test case. Good luck. Hint: You should be a bit careful when counting...
|
algorithms
|
def secret_number(n):
return bin(n). count(str(n % 2)) * * 2
|
Secret problems with numbers
|
64bd5ff1bb8f1006708e545e
|
[
"Algorithms",
"Logic",
"Puzzles",
"Fundamentals"
] |
https://www.codewars.com/kata/64bd5ff1bb8f1006708e545e
|
7 kyu
|
**Introduction:**
You've got a 16-bit calculating machine, but it's old and rusty. It has four 16-bit registers (`R0`, `R1`, `R2`, `R3`) and can do only a NAND operation.
#### Machine Functions:
This machine can perform these actions:
- `read()`: Grabs the next number from a tape and stores it in `R0`. Returns true if it succeeds, false if the tape is empty.
- `output()`: Returns the number stored in `R0` but can only be used once.
- `nand(target, arg1, arg2)`: Calculates (`arg1` NAND `arg2`) and saves the result in the `target` register. Both `arg1` and `arg2` can be either register identifiers, or plain numbers from `0` to `65535`. `target` can only be register identifier `R0`, `R1`, `R2`, `R3` (see the initial solution for more information). It doesn't return anything. Can be called no more than `400 000` times.
- `dump()`: Prints the contents of the registers and tape for debugging purposes. It doesn't return anything.
#### Machine Registers:
`R0`, `R1`, `R2`, `R3` are 16-bit registers that can hold numbers from 0 to 65535. You can't directly read/write them; you can only use them as arguments for the `nand` method.
#### The Task:
Your goal is to find the missing number in a sequence of shuffled integers from `0` to an unknown `n` (0 <= n <= 65535). You need to write a function that takes a 'Machine' instance as an argument. The machine already has a tape loaded, which you can read with the `read` method, perform `nand` operations, and return the missing number using the `output` method. The registers are all set to zero initially, so you don't need to initialize them.
#### Constraints:
You can't simply add the numbers to find the missing one. You must use NAND operations blindly and make only one pass through the tape, and `output()` can only be used once.
The `nand()` method can be called no more than `400 000` times per test.
**Additional Resources:**
This resource may be helpful: [Nand2Tetris Course](https://www.nand2tetris.org/course).
### Example tapes
```
tape result
[3, 2, 1, 4] ---> should return 0
[3, 0, 2, 4] ---> should return 1
[3, 0, 1, 4] ---> should return 2
[0, 2, 1, 4] ---> should return 3
[3, 0, 2, 1] ---> should return 4
[3, 0, 2, 1, 4] ---> should return 5
[] ---> should return 0 for empty tape
```
Good luck and have fun!
|
algorithms
|
def find_missing_number(m):
L, s = 0, 0
while m . read():
L += 1
s ^= L
m . nand(m . R1, m . R0, m . R3)
m . nand(m . R2, m . R0, m . R1)
m . nand(m . R1, m . R1, m . R3)
m . nand(m . R3, m . R2, m . R1)
m . nand(m . R0, m . R3, 65535)
s ^= (~ m . output()) & 65535
return s
|
Find the Missing Number using NAND
|
64be81b50abf66c0147de761
|
[
"Logic",
"Mathematics",
"Restricted"
] |
https://www.codewars.com/kata/64be81b50abf66c0147de761
|
5 kyu
|
A **hexagonal grid** is a commonly used **game board design** based on hexagonal tiling. In the following grid, the two marked locations have a minimum distance of 6 because at least 6 steps are needed to reach the second location starting from the first one.

Write a function that takes a hexagonal grid with two marked locations as input and returns their distance.
The input grid will be a list of strings in which each tile is represented with `o` and the two marked locations with `x`.
### Examples
```
hexDistance([
" o o ",
" o x o ",
" o x ",
]) ➞ 1
hexDistance([
" o o ",
" x o o ",
" o x ",
]) ➞ 2
hexDistance([
" o o o ",
" o o o o ",
" o o o o o ",
" x o o x ",
" o o o ",
]) ➞ 3
hexDistance([
" o x ",
" o o o ",
"o o x o",
" o o o ",
" o o "
]) ➞ 2
hexDistance([
" o x ",
" o o o ",
"o o o o",
" o o o ",
" x o "
]) ➞ 4
```
|
games
|
def hex_distance(grid):
flat = "" . join(grid)
size = len(grid[0])
# find start + end coordinates
start = flat . find("x")
end = flat[start + 1:]. find("x") + start + 1
x1, y1 = divmod(start, size)
x2, y2 = divmod(end, size)
# calculate distance
dx = x2 - x1
dy = abs(y2 - y1)
dy = max(dy - dx, 0) / / 2
return dx + dy
|
Hexagonal Grid: Distance
|
64be6f070381860017dba5ab
|
[
"Arrays",
"Games",
"Logic"
] |
https://www.codewars.com/kata/64be6f070381860017dba5ab
|
6 kyu
|
# Task
The **centered polygonal numbers** are a family of sequences of 2-dimensional figurate numbers, each formed by a central dot, sorrounded by polygonal layers with a constant number of sides. Each side of a polygonal layer contains one dot more than a side in the previous layer.
 | 
- | -
Centered triangular numbers | Centered square numbers
 | 
Centered pentagonal numbers | Centered hexagonal numbers
In the following table are listed the first 12 terms of the sequences of centered _k_-polygonal numbers, with _k_ from 3 to 22:
k | Name | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11
-:| - | -:| -:| -:| -:| -:| -:| -:| -:| -:| -:| -:| -:
3 | Triangular | 1 | 4 | 10 | 19 | 31 | 46 | 64 | 85 | 109 | 136 | 166 | 199
4 | Square | 1 | 5 | 13 | 25 | 41 | 61 | 85 | 113 | 145 | 181 | 221 | 265
5 | Pentagonal | 1 | 6 | 16 | 31 | 51 | 76 | 106 | 141 | 181 | 226 | 276 | 331
6 | Hexagonal | 1 | 7 | 19 | 37 | 61 | 91 | 127 | 169 | 217 | 271 | 331 | 397
7 | Heptagonal | 1 | 8 | 22 | 43 | 71 | 106 | 148 | 197 | 253 | 316 | 386 | 463
8 | Octagonal | 1 | 9 | 25 | 49 | 81 | 121 | 169 | 225 | 289 | 361 | 441 | 529
9 | Nonagonal | 1 | 10 | 28 | 55 | 91 | 136 | 190 | 253 | 325 | 406 | 496 | 595
10 | Decagonal | 1 | 11 | 31 | 61 | 101 | 151 | 211 | 281 | 361 | 451 | 551 | 661
11 | Hendecagonal | 1 | 12 | 34 | 67 | 111 | 166 | 232 | 309 | 397 | 496 | 606 | 727
12 | Dodecagonal | 1 | 13 | 37 | 73 | 121 | 181 | 253 | 337 | 433 | 541 | 661 | 793
13 | Tridecagonal | 1 | 14 | 40 | 79 | 131 | 196 | 274 | 365 | 469 | 586 | 716 | 859
14 | Tetradecagonal | 1 | 15 | 43 | 85 | 141 | 211 | 295 | 393 | 505 | 631 | 771 | 925
15 | Pentadecagonal | 1 | 16 | 46 | 91 | 151 | 226 | 316 | 421 | 541 | 676 | 826 | 991
16 | Hexadecagonal | 1 | 17 | 49 | 97 | 161 | 241 | 337 | 449 | 577 | 721 | 881 | 1057
17 | Heptadecagonal | 1 | 18 | 52 | 103 | 171 | 256 | 358 | 477 | 613 | 766 | 936 | 1123
18 | Octadecagonal | 1 | 19 | 55 | 109 | 181 | 271 | 379 | 505 | 649 | 811 | 991 | 1189
19 | Enneadecagonal | 1 | 20 | 58 | 115 | 191 | 286 | 400 | 533 | 685 | 856 | 1046 | 1255
20 | Icosagonal | 1 | 21 | 61 | 121 | 201 | 301 | 421 | 561 | 721 | 901 | 1101 | 1321
21 | Icosihenagonal | 1 | 22 | 64 | 127 | 211 | 316 | 442 | 589 | 757 | 946 | 1156 | 1387
22 | Icosidigonal | 1 | 23 | 67 | 133 | 221 | 331 | 463 | 617 | 793 | 991 | 1211 | 1453
As you can see:
- 6 is the 1st _pentagonal number_;
- 16 is the 2nd _pentagonal number_ and the 1st _pentadecagonal number_;
- 19 is the 3rd _triangular number_, the 2nd _hexagonal number_ and the 1st _octadecagonal number_.
Write a function that takes an integer `n` as argument and returns its classification as polygonal number:
- return a list whose generic element is a string formatted as `"{i}th {k}-gonal number"` if `n` is the _i_-th _k_-gonal number, in _k_-ascending order;
### Examples
```
isPolygonal(4) ➞ ["1st 3-gonal number"]
is_polygonal(5) ➞ ["1st 4-gonal number"]
isPolygonal(16) ➞ ["2nd 5-gonal number", "1st 15-gonal number"]
is_polygonal(37), ["3rd 6-gonal number", "2nd 12-gonal number", "1st 36-gonal number"]
```
### Notes
- 4 <= n <= 10^10
- you might be interested in [the following kata](https://www.codewars.com/kata/52dda52d4a88b5708f000024) to format English ordinal suffixes.
|
reference
|
def is_polygonal(n):
a = 1
th = "4567890"
poly = []
while (a * (a + 1) / 2) < n - 1:
num_check = (n - 1) / (a * (a + 1) / 2)
if num_check . is_integer() and num_check > 2:
if 10 <= a % 100 <= 20 or str(a)[len(str(a)) - 1:] in th:
poly . append(f" { int ( a )} th { int ( num_check )} -gonal number")
elif str(a)[len(str(a)) - 1:] == "1":
poly . append(f" { int ( a )} st { int ( num_check )} -gonal number")
elif str(a)[len(str(a)) - 1:] == "2":
poly . append(f" { int ( a )} nd { int ( num_check )} -gonal number")
elif str(a)[len(str(a)) - 1:] == "3":
poly . append(f" { int ( a )} rd { int ( num_check )} -gonal number")
a += 1
return poly[:: - 1]
|
Centered Polygonal Number
|
64be5c99c9613c0329bc7536
|
[
"Mathematics",
"Performance"
] |
https://www.codewars.com/kata/64be5c99c9613c0329bc7536
|
5 kyu
|
### Background
**Nerdle** is like Wordle, but for arithmetic expressions rather than words. The idea is to identify a target expression using feedback from previous guesses. In this kata we play the simplest form of Nerdle, where the target expression consists of 5 characters: A digit, followed by an arithmetic operator (either multiplication, division, addition, or subtraction), followed by another digit, then an equals sign, then the result of the computation (which must be a single digit). Examples of such expressions are '1+2=3', '7\*0=0', '9-3=6', '8\/2=4', and so on.
This version of Nerdle is called "Micro-Nerdle". You can play different versions of Nerdle at [the Nerdle website](https://nerdlegame.com/game). The general version of Nerdle, where the expression has 8 characters, is a much harder kata - [Nerdle - The General Version](https://www.codewars.com/kata/64c16111b57ecf13c2e1031e). It might also be worth looking at this Wordle kata - [Wordle! Cheat bot](https://www.codewars.com/kata/6255e6f2c53cc9001e5ef629).
Suppose you guess '1+2=3' and receive the feedback 'RBBGB'. In this notation 'B' means that the character is not present in the target expression, 'R' means that the character is present but in the wrong position, and 'G' means that the character is in the correct position. So we can infer the following about the target expression:
<ol>
<li>It contains at least one 1, but not in the first position.
<li>It doesn't contains a + sign, a 2, or a 3.
<li>It has an equals sign in the fourth position. (This will always be true in Micro-Nerdle.)
</ol>
Using this information, we construct another guess, receive feedback, and so on, until we have identified the target expression. The task in this kata is to program an "intelligent" agent, represented by a function *solve_micro_nerdle*, that successfully plays Micro-Nerdle.
### Input
Your function is provided with a single input called **history** - a list of tuples containing previous guesses and the feedback each one received. The feedbacks are guaranteed to have been computed using a fixed target expression.
### Output
Your function should output a new guess - a string of 5 characters representing an expression in the format above. The goal is for the guess to match the target expression.
### Testing
The testing framework does the following. First *solve_micro_nerdle* is called with **history = [ ]**, i.e. no previous guesses. It should generate some valid expression, call that **guess1**, and the testing code computes the feedback. It then calls *solve_micro_nerdle* with **history = [(guess1, feedback1)]**, and receives a second guess, **guess2**. That guess and feedback are added to the history, creating **history = [(guess1, feedback1), (guess2, feedback2)]**, and *solve_micro_nerdle* is called with that history. This process continues until either *solve_micro_nerdle*'s output matches the target - a success, or when *solve_micro_nerdle* has been called 10 times without matching the target - a failure.
NOTE: To succeed at this kata each case must be solved within 10 attempts AND the average number of attempts over all tests must be lower than 5.
### Details
(1) If the output of any call of *solve_micro_nerdle* is not a valid expression, the feedback will be a string indicating why it's not valid. If this happens, (guess, feedback) is still added to **history** in the usual way, but it's a wasted guess, since it provides no information about the target. In particular, a valid expression must be a correct calculation. For example, a guess like '1+2=8' is invalid, and its feedback is "'1+2' evaluates to 3, NOT 8!"
(2) Your function will only be called with **history** containing its own previous guesses. If you make sure that it never outputs an invalid expression, you don't have to worry about dealing with input histories containing invalid guesses.
(3) Division is real division, not integer division. So an expression like '5/2=2' is invalid; its feedback is "'5/2' evaluates to 2.5, which is not an integer!" Divisions like '8/2=4' are fine. Any division by 0 is invalid.
(4) Commutative solutions are treated as correct. For example, if the target is 2\*3=6, then 3\*2=6 matches the target. However, all feedback is computed on the basis of the actual target, not commutative versions of it. For example, if the target is 2\*3=6 and the guess is 5+2=7, the 2 receives 'R', not 'G'.
### Examples
Here are two examples of an agent nerdling its way to the target.
```
Guess 1 was 1+2=3 Feedback is BBBGG
Guess 2 was 7*0=0 Feedback is GBBGB
Guess 3 was 7-3=4 Feedback is GGRGR
Guess 4 was 7-4=3 Feedback is GGGGG
Congratulations! Target was 7-4=3. You got it in 4 attempts.
Guess 1 was 1+2=3 Feedback is RBBGB
Guess 2 was 1*9=9 Feedback is RGBGB
Guess 3 was 1*0=0 Feedback is RGBGB
Guess 4 was 7*1=7 Feedback is BGGGB
Guess 5 was 6*1=6 Feedback is BGGGB
Guess 6 was 5*1=5 Feedback is BGGGB
Guess 7 was 8*1=8 Feedback is GGGGG
Congratulations! Target was 8*1=8. You got it in 7 attempts.
```
### Duplicates
Understanding the feedback when there are duplicate digits in the guess or target can be tricky. For example:
(a) Suppose guess is '1-1=0' and feedback is 'BBGGB'. The first 1 is 'B' and the second is 'G'. It would be incorrect to infer from the first 1 being 'B' that there is no 1 in the target, because guess contains a second 1. So a 'B' really means "not present in the target, once all other occurrences of the same character in guess have been accounted for".
(b) Suppose guess is '1+1=2' and feedback is 'RBGGR'. The first 1 is 'R' and the second is 'G'. The first 1 being 'R' tells you that there is a second 1 in the target, and it's not in first position. If there wasn't, the first 1 would be 'B', as in (a). So a good next guess is '2-1=1'.
(c) Suppose guess is '1+1=2' and feedback is 'GBGGB'. Both 1s are 'G', and the last character is not 2. It's easy to overlook that the last character could also be a 1 (e.g. target might be '1\*1=1').
|
games
|
TREE = {'guess': '1+2=3', 'feedback': {'GGGGG': {'val': '1+2=3'}, 'GGBGR': {'val': '1+3=4'}, 'GGBGB': {'guess': '1+2=3', 'feedback': {'GGBGB': {'guess': '1+3=4', 'feedback': {'GGBGR': {'val': '1+4=5'}, 'GGBGB': {'guess': '2+6=8', 'feedback': {'BGRGB': {'val': '1+5=6'}, 'BGGGB': {'val': '1+6=7'}, 'BGBGG': {'val': '1+7=8'}, 'BGBGR': {'val': '1+8=9'}, 'BGBGB': {'val': '1+0=1'}}}}}}}, 'BBRGR': {'guess': '1+2=3', 'feedback': {'BBRGR': {'guess': '1+2=3', 'feedback': {'BBRGR': {'guess': '1+5=6', 'feedback': {'BBBGG': {'val': '2*3=6'}, 'BBRGB': {'val': '5-3=2'}, 'BBBGR': {'val': '6/3=2'}}}}}}}, 'BBRGB': {'guess': '1+2=3', 'feedback': {'BBRGB': {'guess': '1+3=4', 'feedback': {'BBBGR': {'guess': '1+7=8', 'feedback': {'BBBGG': {'val': '2*4=8'}, 'BBBGB': {'val': '6-4=2'}, 'BBBGR': {'val': '8/4=2'}}}, 'BBBGB': {'guess': '7-1=6', 'feedback': {'GGBGB': {'val': '7-5=2'}, 'BGBGR': {'val': '8-6=2'}, 'RGBGB': {'val': '9-7=2'}, 'BBBGB': {'val': '2*0=0'}, 'BGBGB': {'val': '2-0=2'}}}}}}}, 'RGRGG': {'val': '2+1=3'}, 'BGRGR': {'val': '2+3=5'}, 'BGRGB': {'guess': '1+2=3', 'feedback': {'BGRGB': {'guess': '1+2=3', 'feedback': {'BGRGB': {'guess': '1+6=7', 'feedback': {'BGRGB': {'val': '2+4=6'}, 'BGBGG': {'val': '2+5=7'}, 'BGGGB': {'val': '2+6=8'}, 'BGBGR': {'val': '2+7=9'}, 'BGBGB': {'val': '2+0=2'}}}}}}}, 'BBGGR': {'val': '3*2=6'}, 'RGBGR': {'val': '3+1=4'}, 'BGGGR': {'val': '3+2=5'}, 'BGBGR': {'guess': '1+2=3', 'feedback': {'BGBGR': {'guess': '1+3=4', 'feedback': {'BGRGR': {'val': '3+4=7'}, 'BGRGB': {'guess': '1+4=5', 'feedback': {'BGBGR': {'val': '3+5=8'}, 'BGBGB': {'val': '3+6=9'}}}, 'BGGGR': {'val': '4+3=7'}, 'BGGGB': {'guess': '1+5=6', 'feedback': {'BGRGB': {'val': '5+3=8'}, 'BGBGR': {'val': '6+3=9'}, 'BGBGG': {'val': '3+3=6'}}}}}}}, 'RBRGR': {'val': '3-1=2'}, 'RBGGR': {'val': '3-2=1'}, 'BBGGB': {'guess': '1+2=3', 'feedback': {'BBGGB': {'guess': '1+3=4', 'feedback': {'BBBGR': {'guess': '3-1=2', 'feedback': {'BBBGR': {'val': '4*2=8'}, 'BGBGG': {'val': '4-2=2'}, 'BBBGG': {'val': '4/2=2'}}}, 'BBBGG': {'guess': '2*3=6', 'feedback': {'RBBGR': {'val': '6-2=4'}, 'RBBGB': {'val': '8/2=4'}, 'GGBGB': {'val': '2*2=4'}}}, 'BBBGB': {'guess': '7*0=0', 'feedback': {'GBBGB': {'val': '7-2=5'}, 'BBBGB': {'val': '8-2=6'}, 'RBBGB': {'val': '9-2=7'}, 'BGRGG': {'val': '0*2=0'}, 'BBRGG': {'val': '0/2=0'}, 'BBBGG': {'val': '2-2=0'}}}}}}}, 'RGBGB': {'guess': '1+2=3', 'feedback': {'RGBGB': {'guess': '1+3=4', 'feedback': {'RGBGR': {'val': '4+1=5'}, 'RGBGB': {'guess': '6+2=8', 'feedback': {'RGBGB': {'val': '5+1=6'}, 'GGBGB': {'val': '6+1=7'}, 'BGBGG': {'val': '7+1=8'}, 'BGBGR': {'val': '8+1=9'}, 'BGBGB': {'val': '0+1=1'}}}}}}}, 'BGGGB': {'guess': '1+2=3', 'feedback': {'BGGGB': {'guess': '1+3=4', 'feedback': {'BGBGR': {'val': '4+2=6'}, 'BGBGB': {'guess': '1+6=7', 'feedback': {'BGBGG': {'val': '5+2=7'}, 'BGRGB': {'val': '6+2=8'}, 'BGBGR': {'val': '7+2=9'}, 'BGBGB': {'val': '0+2=2'}}}, 'BGBGG': {'val': '2+2=4'}}}}}, 'BGBGB': {'guess': '1+4=5', 'feedback': {'BGRGR': {'val': '4+5=9'}, 'BGGGR': {'val': '5+4=9'}, 'BGGGB': {'guess': '1+2=3', 'feedback': {'BGBGB': {'guess': '1+3=4', 'feedback': {'BGBGG': {'val': '0+4=4'}, 'BGBGR': {'val': '4+4=8'}}}}}, 'BGBGG': {'guess': '1+2=3', 'feedback': {'BGBGB': {'guess': '1+5=6', 'feedback': {'BGGGB': {'val': '0+5=5'}, 'BGRGB': {'val': '5+0=5'}}}}}, 'BGBGB': {'guess': '1+6=7', 'feedback': {'BGGGB': {'val': '0+6=6'}, 'BGBGG': {'guess': '1+7=8', 'feedback': {'BGGGB': {'val': '0+7=7'}, 'BGRGB': {'val': '7+0=7'}}}, 'BGBGB': {'guess': '9-8=1', 'feedback': {'BBGGB': {'val': '0+8=8'}, 'RBBGB': {'val': '0+9=9'}, 'BBRGB': {'val': '8+0=8'}, 'GBBGB': {'val': '9+0=9'}, 'BBBGB': {'val': '0+0=0'}}}, 'BGRGB': {'val': '6+0=6'}}}, 'BGRGB': {'val': '4+0=4'}}}, 'RBBGG': {'guess': '1+2=3', 'feedback': {'RBBGG': {'guess': '1+2=3', 'feedback': {'RBBGG': {'guess': '2*4=8', 'feedback': {'BBRGB': {'val': '4-1=3'}, 'BGBGB': {'val': '3*1=3'}, 'BBBGB': {'val': '3/1=3'}}}}}}}, 'RBBGR': {'guess': '1+2=3', 'feedback': {'RBBGR': {'guess': '1+2=3', 'feedback': {'RBBGR': {'guess': '1+3=4', 'feedback': {'RBGGR': {'val': '4-3=1'}, 'RBGGB': {'val': '3/3=1'}}}}}}}, 'RBBGB': {'guess': '1+4=5', 'feedback': {'RBRGR': {'val': '5-1=4'}, 'RBGGR': {'val': '5-4=1'}, 'RBBGG': {'guess': '1+2=3', 'feedback': {'RBBGB': {'guess': '2*3=6', 'feedback': {'BBBGR': {'val': '6-1=5'}, 'BGBGB': {'val': '5*1=5'}, 'BBBGB': {'val': '5/1=5'}}}}}, 'RBBGR': {'guess': '1+2=3', 'feedback': {'RBBGB': {
'guess': '1+5=6', 'feedback': {'RBGGR': {'val': '6-5=1'}, 'RBGGB': {'val': '5/5=1'}}}}}, 'RBBGB': {'guess': '6+1=7', 'feedback': {'RBGGR': {'val': '7-1=6'}, 'RBRGR': {'val': '7-6=1'}, 'BBGGG': {'guess': '2*4=8', 'feedback': {'BBBGR': {'val': '8-1=7'}, 'BGBGB': {'val': '7*1=7'}, 'BBBGB': {'val': '7/1=7'}}}, 'BBRGR': {'guess': '1+7=8', 'feedback': {'RBGGR': {'val': '8-7=1'}, 'RBGGB': {'val': '7/7=1'}}}, 'BBGGB': {'guess': '8*0=0', 'feedback': {'RBBGB': {'val': '9-1=8'}, 'BGRGG': {'val': '0*1=0'}, 'BBRGG': {'val': '0/1=0'}, 'GGBGB': {'val': '8*1=8'}, 'GBBGB': {'val': '8/1=8'}, 'BGBGB': {'val': '9*1=9'}, 'BBBGB': {'val': '9/1=9'}}}, 'BBRGB': {'guess': '1+8=9', 'feedback': {'RBGGR': {'val': '9-8=1'}, 'RBGGB': {'val': '8/8=1'}, 'RBBGR': {'val': '9/9=1'}}}, 'GBGGB': {'guess': '2*3=6', 'feedback': {'BGBGG': {'val': '6*1=6'}, 'BBBGG': {'val': '6/1=6'}}}, 'GBRGB': {'val': '6/6=1'}}}, 'RBRGB': {'guess': '1+2=3', 'feedback': {'RBBGB': {'guess': '2*3=6', 'feedback': {'BGBGB': {'val': '4*1=4'}, 'BBBGB': {'val': '4/1=4'}}}}}, 'RBGGB': {'val': '4/4=1'}}}, 'BBGGG': {'guess': '1+2=3', 'feedback': {'BBGGG': {'guess': '1+2=3', 'feedback': {'BBGGG': {'guess': '1+4=5', 'feedback': {'BBBGR': {'val': '5-2=3'}, 'BBBGB': {'val': '6/2=3'}}}}}}}, 'BBBGR': {'guess': '1+2=3', 'feedback': {'BBBGR': {'guess': '1+3=4', 'feedback': {'BBGGG': {'val': '7-3=4'}, 'BBGGB': {'guess': '0*5=0', 'feedback': {'BBRGB': {'val': '8-3=5'}, 'BBBGB': {'val': '9-3=6'}, 'GGBGG': {'val': '0*3=0'}, 'GBBGG': {'val': '0/3=0'}, 'BGBGB': {'val': '3*3=9'}, 'BBBGG': {'val': '3-3=0'}}}, 'BBRGB': {'val': '3*0=0'}}}}}, 'BBBGG': {'guess': '1+2=3', 'feedback': {'BBBGG': {'guess': '1+3=4', 'feedback': {'BBRGR': {'val': '7-4=3'}, 'BBRGB': {'guess': '1+5=6', 'feedback': {'BBGGB': {'val': '8-5=3'}, 'BBBGR': {'val': '9-6=3'}, 'BBBGB': {'val': '3-0=3'}}}, 'BBGGB': {'guess': '1+5=6', 'feedback': {'BBBGR': {'val': '6-3=3'}, 'BBBGB': {'val': '9/3=3'}}}}}}}, 'BBBGB': {'guess': '1+5=6', 'feedback': {'BBRGB': {'guess': '1+2=3', 'feedback': {'BBBGB': {'guess': '1+4=5', 'feedback': {'BBGGG': {'val': '9-4=5'}, 'BBBGR': {'val': '5*0=0'}, 'BBBGG': {'val': '5-0=5'}}}}}, 'BBGGB': {'guess': '1+2=3', 'feedback': {'BBBGB': {'guess': '0*1=0', 'feedback': {'BBBGB': {'val': '9-5=4'}, 'GGBGG': {'val': '0*5=0'}, 'GBBGG': {'val': '0/5=0'}, 'BBBGG': {'val': '5-5=0'}}}}}, 'BBBGB': {'guess': '2*4=8', 'feedback': {'BGGGB': {'val': '0*4=0'}, 'BGBGB': {'guess': '9-7=2', 'feedback': {'BBGGB': {'val': '0*7=0'}, 'RBBGB': {'val': '0*9=0'}, 'BBRGB': {'val': '7*0=0'}, 'GBBGB': {'val': '9*0=0'}, 'BBBGB': {'val': '0*0=0'}}}, 'BGBGR': {'guess': '1+8=9', 'feedback': {'BBGGB': {'val': '0*8=0'}, 'BBRGB': {'val': '8*0=0'}}}, 'BBGGB': {'guess': '3-1=2', 'feedback': {'BBBGB': {'val': '0/4=0'}, 'BGBGB': {'val': '4-4=0'}}}, 'BBBGB': {'guess': '0/7=0', 'feedback': {'GGGGG': {'val': '0/7=0'}, 'GGBGG': {'val': '0/9=0'}, 'RBRGB': {'val': '7-0=7'}, 'BBGGG': {'val': '7-7=0'}, 'RBBGB': {'val': '9-0=9'}, 'BBBGG': {'val': '9-9=0'}, 'GBBGG': {'val': '0-0=0'}}}, 'BBBGR': {'guess': '3-1=2', 'feedback': {'BBBGB': {'val': '0/8=0'}, 'BGBGB': {'val': '8-8=0'}}}, 'BGRGB': {'val': '4*0=0'}, 'BBRGB': {'val': '4-0=4'}, 'BBBGG': {'val': '8-0=8'}, 'BBGGR': {'val': '8-4=4'}}}, 'BBBGR': {'guess': '1+2=3', 'feedback': {'BBBGB': {'guess': '0*1=0', 'feedback': {'GGBGG': {'val': '0*6=0'}, 'GBBGG': {'val': '0/6=0'}, 'RGBGG': {'val': '6*0=0'}, 'BBBGG': {'val': '6-6=0'}}}}}, 'BBBGG': {'val': '6-0=6'}}}, 'BGBGG': {'guess': '1+2=3', 'feedback': {'BGBGG': {'guess': '1+2=3', 'feedback': {'BGBGG': {'guess': '1+3=4', 'feedback': {'BGGGB': {'val': '0+3=3'}, 'BGRGB': {'val': '3+0=3'}}}}}}}, 'GBBGB': {'guess': '1+4=5', 'feedback': {'GBBGB': {'guess': '6+1=7', 'feedback': {'BBRGB': {'guess': '9-1=8', 'feedback': {'BBRGB': {'val': '1*0=0'}, 'BBRGG': {'val': '1*8=8'}, 'RBRGB': {'val': '1*9=9'}, 'BGRGB': {'val': '1-0=1'}}}, 'RBRGB': {'val': '1*6=6'}, 'BBRGG': {'val': '1*7=7'}, 'BBGGB': {'guess': '0*1=0', 'feedback': {'BBGGG': {'val': '1-1=0'}, 'BGGGB': {'val': '1*1=1'}, 'BBGGB': {'val': '1/1=1'}}}}}, 'GBGGB': {'val': '1*4=4'}, 'GBBGG': {'val': '1*5=5'}}}, 'GBGGB': {'val': '1*2=2'}, 'GBBGG': {'val': '1*3=3'}, 'GGRGB': {'val': '1+1=2'}, 'RBRGB': {'guess': '1+2=3', 'feedback': {'RBRGB': {'guess': '1+2=3', 'feedback': {'RBRGB': {'guess': '6/3=2', 'feedback': {'BBBGG': {'val': '2*1=2'}, 'BBBGR': {'val': '2-1=1'}, 'BGBGG': {'val': '2/1=2'}}}}}}}, 'RBGGB': {'val': '2/2=1'}}}
def solve_micro_nerdle(history):
tree = TREE
for p, v in history:
tree = tree['feedback'][v]
return tree.get('val', tree.get('guess', None))
|
Play Nerdle - It's Wordle for Calculations
|
64b84ed4b46f91004b493d87
|
[
"Strings",
"Games",
"Artificial Intelligence"
] |
https://www.codewars.com/kata/64b84ed4b46f91004b493d87
|
5 kyu
|
# Prelude
The painting fence problem involves finding the number of ways to paint a fence with `n` posts and `k` colors, assuming that no more than two adjacent posts have the same color.
# Task
Your task is to implement a function named ways(n, k) that takes two BigInts as input:
+ `n` The number of posts in the fence.
+ `k` The number of colors available for painting the fence.
And returns the number of ways of painting the fence such that no more than two adjacent posts have the same color.
A linear time solution is much too slow for this problem; the numbers will be up to 10 billion!
# Examples
```javascript
ways(1n, 4n) -> 4n
ways(3n, 2n) -> 6n
ways(4n, 5n) -> 580n
```
# Constraints
`n` and `k` will not be greater than 10,000,000,000 or less than 1.<br>
# Note, result will get very large, return it mod 1000000007
|
algorithms
|
import numpy as np
MOD = 1000000007
def matrix_exp(Q, n):
if n == 0:
return np . array([[1, 0], [0, 1]], dtype=object)
return (Q @ matrix_exp(Q, n - 1) if n & 1 else matrix_exp((Q @ Q) % MOD, n >> 1)) % MOD
def ways(n, k):
return (matrix_exp(np . array([[k - 1, k - 1],
[1, 0]], dtype=object), n - 1) @ np . array([k * k, k], dtype=object))[1] % MOD
|
Painting Fence Algorithm (Number of Ways To Paint A Fence)
|
64bc4a428e1e9570fd90ed0d
|
[
"Dynamic Programming",
"Performance"
] |
https://www.codewars.com/kata/64bc4a428e1e9570fd90ed0d
|
4 kyu
|
# Task
In abstract set theory, a construction due to von Neumann represents the natural numbers by sets, as follows:
- 0 = [ ] is the empty set
- 1 = 0 ∪ [ 0 ] = [ 0 ] = [ [ ] ]
- 2 = 1 ∪ [ 1 ] = [ 0, 1 ] = [ [ ], [ [ ] ] ]
- n = n−1 ∪ [ n−1 ] = ...
Write a function that receives an integer `n` and produces the representing set.
# Examples
```
rep_set(0) ➞ []
rep_set(1) ➞ [[]]
rep_set(2) ➞ [[], [[]]]
rep_set(3) ➞ [[], [[]], [[], [[ ]]]]
```
# Input Constraints
- 0 <= n <= 15
- Code limit is <= 200 characters for Python and <= 300 characters for TypeScript and JavaScript.
|
reference
|
def rep_set(n):
return [rep_set(k) for k in range(n)]
|
Natural Emptiness
|
64b8c6c09416795eb9fbdcbf
|
[] |
https://www.codewars.com/kata/64b8c6c09416795eb9fbdcbf
|
7 kyu
|
## Introduction
You are in charge of organizing a dinner for your team and you would like it to happen with as many participants as possible, as soon as possible. However, finding a date that works for everyone can be challenging due to their other commitments. In this case, a compromise, referred to as the best acceptable date, would be satisfactory.
➡️ A date is considered *acceptable* if the number of people available on that date is equal to or higher than the number of people not available.
➡️ The *best acceptable date* is the acceptable date with the highest number of available people. We will explain later in a dedicated section some tiebreaking rules to make sure the best acceptable date is unique, if existing.
## Your task
**Your task is to write a solution that takes a *list of available dates for each team member* and returns the best acceptable date. If no such date exists, your solution should return `None`.**
For a team of size `n` the input is a list of lists in the format:
`available = [dates_person_1, ..., dates_person_n]`
For person `i` the available dates ```dates_person_i``` are expressed as a list of integers greater than or equal to 0 (in no particular order). Each integer represents the number of days until the intended date. For example, 0 indicates today, 1 indicates tomorrow, 2 indicates the day after tomorrow, and so on. This notation allows us to focus on the relative days without worrying about specific calendar dates.
➡️ The *attendance* of a date is the number of people that would be available on that date.
Here is an example to illustrate the format and approach:
```text
Example #1:
available = [ [0, 1, 2], [1], [1, 2, 4], [] ]
```
In the above example there are 4 people:
- The first person is available on days 0, 1, and 2; the second person is available only on day 1; the third person is available on days 1, 2, and 4; the fourth person is never available.
- The attendance on day 0 is 1, on day 1 is 3, on day 2 is 2, and on day 4 is 1 (attendance is 0 for any other day not explicitly mentioned).
- For this team of size 4, a date is acceptable if there are at least 2 people available.
- Both day 1 (attendance 3) and day 2 (attendance 2) are acceptable dates.
- Day 1 is the best acceptable date because it has the highest attendance (there are no ties to break because all the other dates have lower attendance).
Here are two more examples:
```text
Example #2:
available = [ [0, 1, 5], [2, 3], [4], [], [0, 1] ]
```
For the team of five people in example #2 you can easily verify (by applying the definition) that there are no acceptable dates. The dinner will not be happening, and your solution should return `None`.
```text
Example #3:
available = [ [3, 6, 7], [3, 6], [6] ]
```
For the team of three people in example #3 there are two acceptable dates: day 3 and day 6. Day 6 is the best acceptable date and its attendance is 3.
## Breaking ties
It could happen that there are multiple acceptable dates with the highest attendance. To resolve such ties, we introduce two rules, which should be *applied in strict order*, i.e. first apply rule 1, and if there is still a tie, then apply rule 2.
### Rule 1: "Reward flexibility"
Let's consider this example with 5 people:
```text
Example #4:
available = [ [0, 1, 2, 3], [2], [0, 2], [3, 4, 6], [1, 3, 6] ]
```
Attendance on each day is as follows:
```text
day 0: attendance 2 (works for person 1 and 2)
day 1: attendance 2 (works for person 1 and 5)
day 2: attendance 3 (works for person 1, 2 and 3, and is acceptable)
day 3: attendance 3 (works for person 1, 4 and 5, and is acceptable)
day 4: attendance 1 (works for person 4)
day 6: attendance 2 (works for person 5)
```
Both day 2 and day 3 are acceptable dates with the same and highest attendance. However, it's important to note that while some people indicated several available dates, others were less flexible, such as person 2 who indicated only one available date.
To break the tie, a fair approach (for lack of a better criteria) is to choose a date that works for team members who are more flexible with dates. The idea is that team members who indicated three dates and none of them worked would be more annoyed compared to those who indicated just one date and it didn't get selected.
➡️ We define the *flexibility* of a person as the number of available dates they indicated. In example #4 above, the flexibility of each person is 4, 1, 2, 3, and 3, respectively.
➡️ The *total flexibility of a date* is the sum of the flexibility of the people who are available on that date. To break the tie, we select the date with the *highest total flexibility*.
Let's calculate the total flexibility for the dates with highest attendance in example #2:
```text
total_flexibility(day 2) is 4 + 1 + 2 = 7
total_flexibility(day 3) is 4 + 3 + 3 = 10
```
Day 3 has the highest total flexibility and is therefore the best acceptable date that your solution should return.
### Rule 2: "The sooner the better"
Let's consider a new example with 4 people:
```text
Example #5:
available = [ [0, 1, 2, 3], [0, 1], [0, 5], [1, 6] ]
day 0: attendance 3 (works for person 1, 2 and 3, and is acceptable)
day 1: attendance 3 (works for person 1, 2 and 4, and is acceptable)
day 2: attendance 1 (works for person 1)
day 5: attendance 1 (works for person 3)
day 6: attendance 1 (works for person 4)
person 1 flexibility: 4 (available on days 0, 1, 2, and 3)
person 2 flexibility: 2 (available on days 0 and 1)
person 3 flexibility: 2 (available on days 0 and 5)
person 4 flexibility: 2 (available on days 1 and 6)
```
In this example, both day 0 and day 1 are the only acceptable dates, and both have an attendance of 3. Let's calculate the total flexibility for those dates:
```text
total_flexibility(day 0) is 4 + 2 + 2 = 8
total_flexibility(day 1) is 4 + 2 + 2 = 8
```
Since both dates have equal total flexibility, rule 1 is not sufficient to break the tie. In this case, because the dinner should happen as soon as possible, we simply choose the earliest date. Therefore, day 0 is the best acceptable date that your solution should return.
No further rules are necessary to break ties, and you have now all the necessary information to code the solution!
|
reference
|
from itertools import chain
def team_dinner(available: list[list[int]]) - > int | None:
res = list(chain . from_iterable(available))
res = {i: res . count(i) for i in res}
result = []
for k, v in res . items():
if v >= len(available) / 2 and v == max(res . values()):
result . append(k)
if not result:
return None
elif len(result) == 1:
return result[0]
else:
res = dict . fromkeys(result, 0)
for day in result:
for person in available:
if day in person:
res[day] += len(person)
result = []
for k, v in res . items():
if v == max(res . values()):
result . append(k)
return sorted(result)[0]
|
Team dinner: find the best acceptable date
|
64b1727867b45c41a262c072
|
[
"Fundamentals"
] |
https://www.codewars.com/kata/64b1727867b45c41a262c072
|
6 kyu
|
# Task
Create a function that returns a number which can block the player from reaching 3 in a row in a game of Tic Tac Toe. The number given as an argument will correspond to a grid of Tic Tac Toe: topleft is 0, topright is 2, bottomleft is 6, and bottomright is 8.
Create a function that takes two numbers a, b and returns another number.
This number should be the final one in a line to block the player from winning.
# Examples
```
block_player(0, 3) ➞ 6
block_player(0, 4) ➞ 8
block_player(3, 5) ➞ 4
```
# Notes
The values given will always have two filled squares in a line.
|
algorithms
|
def block_player(a, b):
y1, x1 = divmod(a, 3)
y2, x2 = divmod(b, 3)
y3 = (y2 + (y2 - y1)) % 3
x3 = (x2 + (x2 - x1)) % 3
return y3 * 3 + x3
|
Block the Square in Tic Tac Toe
|
64b7c3e6e0abed000f6cad6c
|
[
"Games",
"Logic",
"Algorithms"
] |
https://www.codewars.com/kata/64b7c3e6e0abed000f6cad6c
|
7 kyu
|
# Task
A staircase is given with a non-negative cost per each step. Once you pay the cost, you can either climb one or two steps. Create a solution to find the minimum sum of costs to reach the top (finishing the payments including `cost[-2]` or `cost[-1]`). You can either start at `cost[0]` or `cost[1]`.
# Examples
```
climbing_stairs([0, 2, 2, 1]) ➞ 2
climbing_stairs([0, 2, 3, 2]) ➞ 3
climbing_stairs([10, 15, 20]) ➞ 15
climbing_stairs([0, 0, 0, 0, 0, 0]) ➞ 0
```
# Notes
- 2 <= len(cost) <= 1000
|
algorithms
|
def climbing_stairs(cost):
a = b = 0
for c in cost:
a, b = b, min(a, b) + c
return min(a, b)
|
Climbing Stairs
|
64b7c03910f916000f493f5d
|
[
"Logic",
"Algorithms",
"Dynamic Programming"
] |
https://www.codewars.com/kata/64b7c03910f916000f493f5d
|
6 kyu
|
# Task
The function is given a list of particles. The absolute value represents the particle mass. The sign of value represents the direction of movement:
- Positive values move to the right.
- Negative values move to the left.
A positive value located on the left will collide with a negative value immediately located on the right. The particle with the greater mass will absorb the mass of another particle and continue to travel in its direction. If the negative is greater, the combined particle will continue to move to the left, if the positive mass is greater or equal, the combined particle will continue to move to the right. The mass of the combined particle is the sum of absolute values. Two particles moving in the same direction cannot collide because it is assumed that the speed is the same before and after collisions. The new combined particles can collide again. The total picture of remaining particles can evolve and evolve.
Eventually, the equilibrium is reached when all negative values are on the left and all positive values are on the right. The left group is moving away from the right group. Determine the equilibrium state of the transformed particles and return it as a list.
# Examples
```
moving_particles([]) ➞ []
# No particles are in the list.
moving_particles([3, -1]) ➞ [4]
# 3 absorbs -1.
moving_particles([-1, 3, -1, 2]) ➞ [-1, 4, 2]
# -1 is moving to the left, 2 is moving to the right, 3 absorbs -1.
moving_particles([5, -1, -2, -9]) ➞ [-17]
# 5 absorbs -1, new 6 absorbs -2, new 8 is being absorbed by -9.
```
# Notes
- The problem is not ideally symmetric. If the masses are the same, the positive mass absorbs the negative mass and continues moving to the right. This assumption is to account for all possibilities.
- List will not contain zeros.
# Input constraints
- Easy : 0<=len(lst)<=20
- Medium : 50<=len(lst)<=200
- Hard : 500<=len(lst)<=1000
|
algorithms
|
def moving_particles(lst):
cur, ls = 0, lst[:]
while cur < len(ls) - 1:
if ls[cur] > 0 and ls[cur + 1] < 0:
ls[cur: cur + 2] = [(ls[cur] - ls[cur + 1]) *
(- 1 if ls[cur] < - ls[cur + 1] else 1)]
cur = max(cur - 1, 0)
else:
cur += 1
return ls
|
Moving Particles
|
64b76b580ca7392eca9f886b
|
[
"Games",
"Logic",
"Algorithms"
] |
https://www.codewars.com/kata/64b76b580ca7392eca9f886b
|
6 kyu
|
# Task
The function is given a list of tuples. Each tuple has two numbers `tpl[0] < tpl[1]`. A chain can be made from these tuples that satisfies the condition: `(n1, n2) -> (n3, n4) -> ...` for each pair of consecutive tuples `n2 < n3`. Find the maximum length of such chain made from the given list.
# Examples
```
len_longest_chain([(2, 3), (3, 4), (3, 5)]) ➞ 1
# Any of the given tuple make a chain of length 1
len_longest_chain([(2, 3), (3, 4), (1, 2)]) ➞ 2
# (1, 2) -> (3, 4) => len_chain = 2
len_longest_chain([(-15, -11), (17, 22), (8, 12), (-11, -10), (-4, -1)]) ➞ 4
# (-15, -11) -> (-4, -1) -> (8, 12) -> (17, 22) => len_chain = 4
len_longest_chain([(-5, 0), (-4, 0), (4, 5), (3, 4), (-1, 1), (-6, -2)]) ➞ 3
# (-6, -2) -> (-1, 1) -> (3, 4) => len_chain = 3
```
# Input Constraints
1<=len(pairs)<=1000
|
algorithms
|
from operator import itemgetter
def len_longest_chain(pairs):
res, x = 0, float('-inf')
for a, b in sorted(pairs, key=itemgetter(1)):
if x < a:
res, x = res + 1, b
return res
|
Find the Maximum Length of a Chain
|
64b779a194167920ebfbdd2e
|
[
"Arrays",
"Logic"
] |
https://www.codewars.com/kata/64b779a194167920ebfbdd2e
|
7 kyu
|
# Task
The function is given a string consisting of a collection of three characters:
- "(" open bracket
- ")" closed bracket
- "J" Joker, which can be replaced by "(", ")" or ""
Develop a solution to determine if the given string represents a proper sequence of parenthesis; return `True / False`. Each open bracket on the left should have a corresponding closed bracket on the right. For example "(()())" is a proper sequence, "()(()" is not a proper sequence. The presence of Jokers adds an extra level of difficulty to the analysis because each "J" makes three possibilities to consider. An empty string is considered a valid string because it does not contain unbalanced brackets.
# Examples
```
closed_brackets("(J))") ➞ True
# J can be replaced with (
closed_brackets("(") ➞ False
# Unbalanced open bracket.
closed_brackets("") ➞ True
# Empty string is a valid sequence.
closed_brackets("()J(") ➞ False
# Not possible to balance the brackets.
closed_brackets("J") ➞ True
# J can be replaced with an empty string.
closed_brackets(")(") ➞ False
# Numbers of ( and ) are the same but they are in the wrong places.
closed_brackets("J)(J") ➞ True
# First 'J' can be replaced with '(' and second with ')'
closed_brackets("()") ➞ True
# A proper sequence of balanced brackets.
```
# Input Constraints
- 0 <= len(s) <= 100
|
reference
|
def closed_brackets(s):
a, b = 0, 0
for c in s:
if c == ")" and b == 0:
return False
a = a + 1 if c == "(" else a and a - 1
b = b - 1 if c == ")" else b + 1
return not a
|
Closed Brackets String
|
64b771989416793927fbd2bf
|
[
"Algorithms",
"Strings",
"Recursion",
"Stacks",
"Dynamic Programming",
"Data Structures"
] |
https://www.codewars.com/kata/64b771989416793927fbd2bf
|
6 kyu
|
Been a while, but here's part 2!
You are given a ```string``` of lowercase letters and spaces that you need to type out. In the string there is a special function: ```[shift]```. Once you encounter a ```[shift]``` , you ```capitalise``` the character right after it, as if you're actually holding the key. Return the final ```string``` .
\
\
e.g. ```[shift]john [shift]green``` return ```John Green``` (capitalise the ```j``` and ```g```)
Walkthrough:
```[shift]```\
J ```capitalise``` the ```j```\
Jo\
Joh\
John\
John[space]\
John G ```capitalise``` the ```g```\
John Gr\
John Gre\
John Gree\
John Green
```John Green```
\
\
e.g. ```[shift]n[shift]o[shift]o[shift]o``` return ```NOOO``` (capitalise all the letters)
Walkthrough:
```[shift]```\
N ```capitalise``` the ```n```\
NO ```capitalise``` the ```O```\
NOO ```capitalise``` the ```O```\
NOOO ```capitalise``` the ```O```
```NOOO```
___
Notice if we want to capitalise a long string of letters, it will look very confusing viually. So, let's add two new functions, ```holdshift``` and ```unshift```. It's self-explanatory.
\
\
Some examples:
```[holdshift]uppercase[unshift]``` return ```UPPERCASE``` (```holdshift``` all letters)
Walkthrough:
```[holdshift]```\
U\
UP\
UPP\
...
UPPERCASE\
```[unshift]```
```UPPERCASE```
\
\
```unshift``` can also apply to normal ```shift```, but since normal ```shift``` only affects the character right after, ```unshift``` would have to be directly after normal ```shift``` for it to affect it.
Example: ```[shift][unshift]dont [shift][unshift]shift``` returns ```dont shift```
Walkthrough:
```[shift][unshift]``` cancels\
dont[space]\
```[shift][unshift]``` cancels\
dont shift
```dont shift```
\
\
Whew! That was lengthy!
Ok, to summerise:
- ```[shift]``` capitalises the character right after it (```[shift]a``` -> ```A```)
- ```[holdshift]``` capitalises all the characters after it until it reaches ```unshift``` (```[holdshift]one[unshift]two``` -> ```ONEtwo```)
- ```[unshift]``` releases shift (either ```[shift]``` or ```[holdshift]```)
- ```[shift][unshift]d``` returns ```d```
Other necessary things you might want to know:
- ```Shifting``` a space is a space
- After a ```[holdshift]```, there is always an ```unshift```, without any functions in between
- After ```unshifting```, the next function called will not be an ```unshift``` (you can't release something if you're not pressing it)
- Things like ```[shift][holdshift]``` or ```[shift][shift]``` or ```[holdshift][shift]```can't occur, but ```[shift][unshift]``` can
- The string will never start with ```[unshift]``` for obvious reasons
Good luck! More examples in the example tests (The description took me way too long lol)
Please give this a good rating, I spent a really long time coding this.
Thank you!
______
Check out <a href="https://www.codewars.com/collections/65abaddba4b9f2013327dd3d">the rest of the kata in this series</a>!
|
algorithms
|
import re
def type_out(src):
dst = src . split('[', 1)[0]
for mo in re . finditer(r'\[(\w+)\]([^\[]+)', src):
match mo[1]:
case 'shift':
dst += mo[2][0]. upper() + mo[2][1:]
case 'holdshift':
dst += mo[2]. upper()
case 'unshift':
dst += mo[2]
return dst
|
Typing series #2 --> the [shift] function
|
64b63c024979c9001f9307e4
|
[] |
https://www.codewars.com/kata/64b63c024979c9001f9307e4
|
6 kyu
|
# Task
The function is given a string consisting of a mix of three characters representing which direction a domino is tilted:
- "R" tilted to the right
- "L" tilted to the left
- "I" standing up, not tilted
The string represents the initial state of the assembly. After a time click the overall state can change. The tilted dominoes tend to tilt their standing-up neighbors. The propagation speed is the same for left and right. The following rules are applied:
- "RI" will change to "RR" unless "I" is being pushed from two opposite directions at the same time.
- "IL" will change to "LL" unless "I" is being pushed from two opposite directions at the same time.
- "RIL" will stay unchanged because "I" is being pushed from two opposite directions at the same time.
- "RIIL" will change to "RRLL" after one click.
- "RR", "LL" "RL" will stay unchanged.
Some "I"s at the ends of the string may stay unaffected if no push came to them.
Determine the final state of the assembly after all propagations have been exhausted and return it as a string (of the same length).
# Examples
```
dominoes_fall("") ➞ ""
# No dominoes in the assembly.
dominoes_fall("RIIII") ➞ "RRRRR"
# Propagation starts on the left causing all others to tilt right.
dominoes_fall("IIIIL") ➞ "LLLLL"
# Propagation starts on the right causing all others to tilt left.
dominoes_fall("RIIIL") ➞ "RRILL"
# After one click second and fourth tilt and then the middle one is pushed by two opposing forces.
dominoes_fall("IRIIL") ➞ "IRRLL"
# The first one has not received any push.
dominoes_fall("IRRIL") ➞ "IRRIL"
# The assembly is already in the final stage. No propagation was launched.
```
# Input constraints
- 0<=len(s)<=30000
- Keep in mind that the state changes time click after time click.
|
games
|
from functools import partial
from re import compile
def helper(x):
r, i, l = x . groups()
if not (l or r):
return i
v = len(i)
if not l:
return "R" * (v + 1)
if not r:
return "L" * (v + 1)
q, r = divmod(v, 2)
return "R" * (q + 1) + "I" * r + "L" * (q + 1)
dominoes_fall = partial(compile(r"(R?)(I+)(L?)"). sub, helper)
|
Let the Dominoes Fall Down
|
64b686e74979c90017930d57
|
[
"Algorithms",
"Logic",
"Regular Expressions",
"Strings"
] |
https://www.codewars.com/kata/64b686e74979c90017930d57
|
6 kyu
|
# Task
The function is given a non-empty balanced parentheses string. Each opening `'('` has a corresponding closing `')'`.
Compute the total score based on the following rules:
- Substring `s == ()` has score `1`, so `"()"` should return `1`
- Substring `s1s2` has total score as score of `s1` plus score of `s2`, so `"()()"` should return `1 + 1 = 2`
- Substring `(s)` has total score as two times score of `s`, so `"(())"` should return `2 * 1 = 2`
Return the total score as an integer.
# Examples
```python
eval_parentheses("()") ➞ 1
# 1
eval_parentheses("(())") ➞ 2
# 2 * 1
eval_parentheses("()()") ➞ 2
# 1 + 1
eval_parentheses("((())())") ➞ 6
# 2 * (2 * 1 + 1)
eval_parentheses("(()(()))") ➞ 6
# 2 * (1 + 2 * 1)
eval_parentheses("()(())") ➞ 3
# 1 + 2 * 1
eval_parentheses("()((()))") ➞ 5
# 1 + 2 * 2 * 1
```
~~~if:lambdacalc
# Encodings
purity: `LetRec`
numEncoding: `BinaryScott`
the input will be encoded as a `List` of `Paren`s:
```lambdacalc
# Paren = OPEN | CLOSE
OPEN = \ open close . open
CLOSE = \ open close . close
```
these definitions are `Preloaded`. note that `Paren` is isomorphic to `Boolean`.
export constructors `nil, cons` for your `List` encoding.
~~~
|
algorithms
|
def eval_parentheses(s):
st = [0]
for c in s:
if c == '(':
st . append(0)
else:
x = st . pop()
st[- 1] += 2 * x or 1
return st . pop()
|
Evaluate the Group of Parentheses
|
64b6722493f1050058dc3f98
|
[
"Algorithms",
"Logic",
"Regular Expressions",
"Strings"
] |
https://www.codewars.com/kata/64b6722493f1050058dc3f98
|
6 kyu
|
# Task
The function is given two equal size matrices of integers. Each cell holds a pixel: 1 represents a black pixel, 0 represents a white pixel. One of the images can be shifted in any two directions (up, down, left, right) relative to the other image by any number of cells, e.g. (2 up, 1 right) or (1 down, 0 left). Determine the maxim possible overlap of black pixels of the two images.
# Examples
```
max_overlap([[1]], [[1]]) ➞ 1
# Each image has only one pixel.
max_overlap([[0]], [[0]]) ➞ 0
# No pixels in any image
max_overlap([[1, 1, 0],
[0, 1, 0]],
[[0, 1, 1],
[0, 0, 1]]) ➞ 3
# The first image can be shifted to the right by 1 to get 3-pixel overlap.
max_overlap([[0, 1, 0],
[1, 1, 0]],
[[0, 1, 1],
[0, 0, 1]]) ➞ 2
# The first image can be shifted 1-right, 1-up to get 2-pixel overlap.
max_overlap([[1, 1],
[1, 1]],
[[0, 0],
[1, 1]]) ➞ 2
# Without any shift a 2-pixel overlap is achieved and it cannot be larger.
```
# Input constraints
- img1[n][m], img2[n][m] where 1<=n<=15, 1<=m<=15
- Images can be of rectangle shapes
|
algorithms
|
from scipy . signal import correlate2d
def max_overlap(img1, img2):
return correlate2d(img1, img2). max()
|
Maximum Overlap of Two Images
|
64b6698c94167906c3fbd6c4
|
[
"Arrays",
"Algorithms",
"Data Structures"
] |
https://www.codewars.com/kata/64b6698c94167906c3fbd6c4
|
6 kyu
|
Gymbro is at a Unique gym with unique bars for Bench pressing. Bars are made up of 40 hyphens ('-') each weighing 0.5kg, represented like this: ``----------------------------------------``
The plates are represented in the format '|Xkg|', where 'X' is the weight of the plate. For Example: ``['|4kg|', '|22kg|', '|10kg|', '|24kg|', '|171kg|']``
*Plates weighing less than 10 kg have length of 5 hyphens, plates weighing between 10 kg and 99 kg have length of 6 hyphens and Plates weighing between 100 kg and 999 kg have length of 7 hyphens.*
Gymbro has a desired weight ``w`` he wants to benchpress, for that he has to put plates on the bar, but You don't actually put plates on the bar, rather, you replace hyphens with plates,
*For example, if you put a 4 kg plate on the bar, it would look like this:*
``--|4kg|---------------------------------`` *length of the bar is still 40*
*5 hyphens were replaced by 4kg plate.*
To calculate the new weight of the bar after adding a plate, you need to subtract the weight of the mini bars that the plate replaces. For instance, if you replaced 5 hyphens (20 kg - 5 * 0.5 kg = 17.5 kg) with a 4 kg plate, the bar's new weight would be 17.5 kg + 4 kg = 21.5 kg.
Rules:
1. *There should be an equal amount of plates on each side*
2. *Plates must always be 2 hyphens away from the edge of the bar on each side.* ``--|4kg||2kg|----------------|13kg||9kg|-`` *is wrong!*
3. *Each plate is available once, but if there are multiple same weighted plates you can use them as many times as it's available*
4. *Weight and Plate distribution matters. Sequentially arrange weight plates from heaviest to lightest,* ``--|30kg||5kg|--------------|7kg||34kg|--`` *biggest plate on the Right, next biggest on the left, next biggest next to biggest and etc, with the heaviest Weight on the Right!!!. Heavier plates should be closer to edges. See more example at test samples*
5. *if there are multiple solutions, output the one which requires the least amount of plates, and which has the least heavy plate ``--|37kg||34kg|------------|36kg||40kg|--`` should equal ``--|39kg||23kg|------------|32kg||53kg|--``, Because second bar has the lightest plate ``23``*.
_________________
*if there is a tie between lightest plates with configurations for example:*
1. ``--|42kg||18kg|------------|27kg||83kg|--``
2. ``--|52kg||18kg|------------|21kg||79kg|--``
return the one which has second lightest plate, If there are 2 ties, and both configs have 2 same weighted light plates, return config which has 3rd lightest plate. *In this case ``--|52kg||18kg|------------|21kg||79kg|--`` would be correct, because while both configurations have* |18kg| *plates, second config has, second lighter plate:* |21kg|
________________
6. Plates shouldn't cross middle point of the bar. Since length of bar is 40, middle point should be 2 hyphens in the middle: ``-------------------*--*-------------------``. * -- * is the middle point. ``--|28kg||28kg||10kg||20kg||28kg||30kg|--`` is wrong. ``--|10kg||1kg||1kg|--|1kg||10kg||100kg|--`` is also wrong since 2 middle hyphens aren't in the center
Your task is to create a function that takes two parameters: ``w`` (the desired weight Gymbro wants to bench, ``targetSum`` in JS) and ``ap`` (a list of available plates, ``WeightList`` in JS). The function should calculate the weight distribution on the bar using the available plates while adhering to the rules mentioned above, and return a visual representation of the bar.
𝗘𝘅𝗮𝗺𝗽𝗹𝗲:
```w``` = 40 *Desired Weight.*
```ap``` = ['|3kg|', '|7kg|', '|1kg|', '|2kg|', '|10kg|', '|4kg|', '|11kg|'] *available plates.*
result = configure_bar(w, ap)
return result
0. Starting bar: ``----------------------------------------`` ``(40 hyphens, each 0.5 kg, Bar weight: 20 kg)``
1. add 10kg:
``--|10kg|--------------------------------`` ``(Replaced 6 '-',new weight:20kg - 6*0.5kg+10kg = 27kg)``
2. add 7kg:
``--|10kg|-------------------------|7kg|--`` ``(Replaced 5 '-', new weight: 27kg-5*0.5kg+7kg=31.5kg)``
3. add 11kg:
``--|10kg|-------------------|7kg||11kg|--`` ``(Replaced 6 '-',weight: 39.5)``
4. add 3kg:
``--|10kg||3kg|--------------|7kg||11kg|--``
`` ( Replaced 5 '-',weight: 40 kg)``
*Output should be:* ``"--|10kg||3kg|--------------|7kg||11kg|--"``
𝗜𝗳 𝗱𝗲𝘀𝗶𝗿𝗲𝗱 𝗯𝗲𝗻𝗰𝗵𝗽𝗿𝗲𝘀𝘀 𝘄𝗲𝗶𝗴𝗵𝘁 𝗰𝗮𝗻'𝘁 𝗯𝗲 𝗮𝗰𝗵𝗶𝗲𝘃𝗲𝗱 𝘄𝗶𝘁𝗵 𝗴𝗶𝘃𝗲𝗻 𝗽𝗹𝗮𝘁𝗲𝘀 𝗼𝗿 𝗮𝗰𝗵𝗶𝗲𝘃𝗶𝗻𝗴 𝗱𝗲𝘀𝗶𝗿𝗲𝗱 𝘄𝗲𝗶𝗴𝗵𝘁 𝗯𝗿𝗲𝗮𝗸𝘀 𝗿𝘂𝗹𝗲𝘀, 𝗿𝗲𝘁𝘂𝗿𝗻``":("``
*in rare cases where Desired weight is 20, don't return an empty bar, return the correct config of the bar using plates, if it can't be achieved return :(*
____________________________________________
Js:
1. 25 fixed tests
2. 866 random test for heavy weights (Plate weight - 10-140,5 - 40 plates, Desired Weight 150 - 300 KG)
3. 800 random test for light weights (plate weight 1-9, 5-30 plates, Desired Weight 20-80)
____________________________________________
Python:
1. 1844 lightweight tests
2. 1534 super-lightweight tests
3. 300 medium weight tests
4. 347 heavyweight tests
5. 300 super heavyweight tests
6. 266 super duper heavyweight tests
|
algorithms
|
from itertools import combinations as combs
def configure_bar(goal, gym):
d = {plate: 2 * int(plate[1: - 3]) - len(str(plate)) for plate in gym}
w = sorted([d[plate] for plate in gym])
s = {v: k for k, v in d . items()}
for n in [2, 4, 6]:
for load in combs(w, n):
if 40 + sum(load) != goal * 2:
continue
right, left = load[1:: 2], load[- 2:: - 2]
r, l = [sum(len(s[p]) for p in side) for side in (right, left)]
if l >= 18 or r >= 18:
return ':('
return f"-- { '' . join ([ s [ p ] for p in left ])}{ '-' * ( 36 - r - l )}{ '' . join ([ s [ p ] for p in right ])} --"
return ':('
|
Gymbro's Unique Gym - Weight Calculator
|
64b41e7c1cefd82a951a303e
|
[
"Algorithms",
"Performance",
"Combinatorics"
] |
https://www.codewars.com/kata/64b41e7c1cefd82a951a303e
|
4 kyu
|
**Intro:**
Hear ye, hear ye! Brave programmers, wizards of the digital realm, I beseech thee to embark upon a quest of prime numbers and mystic algorithms! Prepare thine trusty Python 3.11 swords, for we shall traverse the mystical graph and unveil the **shortest path** betwixt two four-digit prime numbers, but thou shalt also face a series of a hundred randomized trails, culminating in a grand total of 112!
**Primary Objective:**
Fear not, for I shall guide thee in this odyssey of code! Thou shalt construct a grand function, `find_shortest_path`, which shall accept two noble prime numbers as its champions: `start` and `end`. This function, upon completion, shall bestow upon thee a list of integers, revealing the sacred sequence of numbers thou shalt visit on thy journey. Be sure to include both the starting and ending numbers in thy blessed list.
**Example:**
As an example, let us consider the enigma of the numbers `1033` and `8179`. The path to enlightenment shall unfold thusly: `[1033, 1733, 3733, 3739, 3779, 8779, 8179]`. Take heed, for **each number along the path is prime and changes but a single digit at a time.** Nay, worry not, for thou may assumeth that the numbers we provide shall forever be **four-digit prime numbers**.
**Rules:**
* A valid path is comprised of steps, where each step requireth the changing of a single digit in the current number. The digit may be transformed into any other digit betwixt 0 and 9, ye see?
* But beware! The resulting number must also remain a four-digit prime number, for we seek only those graced by the divinities of numbers.
* And remember, only one digit may be altered in each step, and let us forsake the vile leading zeros, for they are an abomination in our realm.
*Now, go forth, noble programmer! May the spirits of the ancients guide thy code and lead thee to victory!*
ps. Thanks to all of the people who created suggestions, found issues in the code, and overall helped with the development of this kata
|
algorithms
|
from collections import defaultdict
from functools import reduce
from itertools import pairwise
from operator import or_
from gmpy2 import is_prime, next_prime
def get_neighbours():
primes = {p for p in range(1000, 9999) if is_prime(p)}
table = defaultdict(list)
for n in primes:
for a, b in pairwise((10_000, 1_000, 100, 10, 1)):
stop = n + a - n % a
for m in range(n + b, stop, b):
if m in primes:
table[n]. append(m)
table[m]. append(n)
return table
neighbours = get_neighbours()
def find_shortest_path(start, end):
paths = {start: [start]}
seen = {start}
while end not in paths:
seen . update(paths)
paths = reduce(or_, ({q: path + [q] for q in neighbours[p]
if q not in seen} for p, path in paths . items()))
return paths[end]
|
Prime Path Finder
|
64b2b04e22ad520058ce22bd
|
[
"Graph Theory",
"Number Theory",
"Algorithms",
"Data Structures",
"Graphs"
] |
https://www.codewars.com/kata/64b2b04e22ad520058ce22bd
|
5 kyu
|
## Introduction
A [seven-segment display](https://en.wikipedia.org/wiki/Seven-segment_display) is an electronic device used to show decimal numerals. It consists of seven segments arranged in a rectangular shape. There are two vertical segments on each side and one horizontal segment at the top, middle, and bottom. By activating specific combinations of segments, the display can represent all decimal digits.
You are working on a maker project involving a seven-segment display component. Your goal is to verify its functionality and understand how it operates.
## Working with segments
Digits are displayed with segments as follows:
```text
_ _ _ _ _ _ _ _
| | | _| _| |_| |_ |_ | |_| |_|
|_| | |_ _| | _| |_| | |_| _|
```
A conventional way to indicate individual segments is to label them with letters `a`, `b`, `c`, `d`, `e`, `f`, `g`, arranged as follows:
```text
aaaa
f b
f b
gggg
e c
e c
dddd
```
Each **segment** can **switch** its state from off to on or vice versa. Depending on the digit currently displayed, certain segments are on and others off. When a new digit is displayed, some segments may switch their state, while others may remain unchanged. Here are a few examples:
- when the display transitions from digit 6 to 8, segment `b` turns on: the number of segment switches is 1.
- when the display transitions from digit 2 to 3, segment `e` turns off and segment `c` turns on: the number of segment switches is 2.
- when the display transitions from blank state to digit 8, all segments turn on: the number of segment switches is 7.
One or more seven-segment displays can be arranged together to compose a **display board**. The amount of displays corresponds to the board **size**. For instance, a display board of size 4 can display any 4-digit number from 0 to 9999. When a number requires less digits then the display board size, it is displayed aligned to the right, and the components for the unused digits are blank.
## Your task
Your task is to write a solution that takes two parameters:
- `size`: the size of the display board, i.e. the number of digits (size can be 1 or more)
- `sequence`: a sequence of integers, each composed of a number of digits between 1 and `size`
and returns the **total number of segment switches performed by the display board throughout the sequence**.
Note initially the display board is blank, meaning all segments for all digit positions are off, and upon completion the last number of the sequence remains displayed.
|
algorithms
|
segments = {
' ': 0b0000000,
'0': 0b1111110,
'1': 0b0110000,
'2': 0b1101101,
'3': 0b1111001,
'4': 0b0110011,
'5': 0b1011011,
'6': 0b1011111,
'7': 0b1110000,
'8': 0b1111111,
'9': 0b1111011
}
def count_segment_switches(display_size, sequence):
old = ' ' * display_size
switches = 0
for i in sequence:
new = str(i). rjust(display_size)
for old_dig, new_dig in zip(old, new):
switches += (segments[old_dig] ^ segments[new_dig]). bit_count()
old = new
return switches
|
Seven-segment display: how many switches?
|
64a6e4dbb2bc0500171d451b
|
[
"Fundamentals"
] |
https://www.codewars.com/kata/64a6e4dbb2bc0500171d451b
|
6 kyu
|
Telepathy:
This is a simple magic trick.
I find it fascinating after watching this magic trick.
Here's how the trick goes:
Firstly, the magician has 6 cards in hand.
Then, the magician asks you to choose a number between 0 and 60 and remember it.
After that, the magician tells you to say "Yes" when you see your chosen number among the cards, otherwise say "No".
Finally, the magician, after listening to all your answers, can sense the number you remembered and reveal it.
Task:
Your task is to play the role of the magician.
I will give you a string representing the audience's answers.
You need to guess the number chosen by the audience.
*** card has multiple numbers written on it and this set of 6 cards never changes.***
```python
"| Card 1: Yes | Card 2: Yes | Card 3: Yes | Card 4: Yes | Card 5: No | Card 6: Yes |" -> 47
```
~~~if:python
Only 1 line of code and 106 characters of code can be used.
~~~
~~~if:kotlin
Only 1 line of code and 135 characters of code can be used.
~~~
~~~if:javascript
Only 1 line of code and 105 characters of code can be used.
~~~
~~~if:coffeescript
Only 1 line of code and 105 characters of code can be used.
~~~
~~~if:typescript
Only 1 line of code and 120 characters of code can be used.
~~~
~~~if:php
Only 1 line of code and 120 characters of code can be used.
~~~
~~~if:c
Only 1 line of code and 150 characters of code can be used.
~~~
~~~if:cpp
Only 1 line of code and 111 characters of code can be used.
~~~
We welcome all codewarriors to leave comments on areas they would like to improve or maintain.
--Good luck codewarrior--
|
games
|
f = magic_show = lambda a: len(a) and (
a[0] == 'Y') - ~ (a[0] in 'YN') * f(a[1:])
|
Telepathy
|
64ad571aa33413003e712168
|
[
"Puzzles",
"Restricted",
"Strings",
"Mathematics"
] |
https://www.codewars.com/kata/64ad571aa33413003e712168
|
6 kyu
|
The emperor of an archipelago nation has asked you to design a network of bridges to connect all the islands of his country together. But he wants to make the bridges out of gold. To see if he can afford it, he needs you to find the shortest total bridge length that can connect all the islands.
Each island's bridges will begin at the same point (the centre of the island), so that all the bridges connect to each other.
```if:python
As your input, you will be provided with the Cartesian coordinates of the centre of each island as a list of (x, y) tuples – for example, an island at (1, 1) is 1 metre north of an island at (1, 0).
```
```if:javascript,julia
As your input, you will be provided with the Cartesian coordinates of the centre of each island as a array of [x, y] arrays – for example, an island at [1, 1] is 1 metre north of an island at [1, 0].
```
Your function should return the minimum total bridge length, in metres, that can connect all the islands.
```if:python,julia
Be warned – this country has a lot of islands, so your algorithm must be fast enough to calculate the bridge lengths for 5000 islands without timing out.
```
```if:javascript
Be warned – this country has a lot of islands, so your algorithm must be fast enough to calculate the bridge lengths for 15,000 islands without timing out.
```
The values of x and y may be any real numbers from -10,000 to 10,000.
```if:python
Disallowed Python modules: SciPy
```
|
algorithms
|
import math
import heapq
class DisjointSetUnion:
def __init__(self, n):
self . parent = list(range(n))
self . size = [1] * n
def find(self, x):
if self . parent[x] != x:
self . parent[x] = self . find(self . parent[x])
return self . parent[x]
def union(self, x, y):
px, py = self . find(x), self . find(y)
if px == py:
return False
if self . size[px] > self . size[py]:
px, py = py, px
self . size[py] += self . size[px]
self . parent[px] = py
return True
# Kruskal’s Minimum Spanning Tree
def bridge(islands):
heap = [(d, i, j) for i, p in enumerate(islands) for j, q in enumerate(
islands[i + 1:], i + 1) if (d := math . dist(p, q)) < 5000]
heapq . heapify(heap)
cost, edges_left = 0, len(islands) - 1
dsu = DisjointSetUnion(len(islands))
while heap:
dist, i, j = heapq . heappop(heap)
if dsu . union(i, j):
cost += dist
edges_left -= 1
if edges_left == 0:
break
return cost
|
Bridge the Islands
|
64a815e3e96dec077e305750
|
[
"Graph Theory",
"Performance"
] |
https://www.codewars.com/kata/64a815e3e96dec077e305750
|
4 kyu
|
  A space agency recently launched a new satellite with the primary goal of identifying the most suitable planet within a given solar system to support human life. The satellite is equipped to scan entire solar systems and add each detected planet to a list. The satellite uses the following format when inputting planets into an array: [elements]_[surface area]. In this format, each element is represented by its chemical symbol from the periodic table. For example, a planet composed of hydrogen (H), oxygen (O), and nitrogen (N), with a surface area of 100 thousand square miles, wouled be labeled as follows:
* `HON_100`
  You will receive a list that includes all the planets in a solar system, as well as an inclusive maximum size that a planet can be for human life. Your task is to identify the planet that possesses all the essential elements for human life while being as large as possible. The required elements for human life are: Hydrogen (H), Carbon (C), Nitrogen (N), Oxygen (O), Phosphorus (P), and Calcium (Ca). These elements are represented as follows:
`["H", "O", "N", "C", "P", "Ca"]`
  If none of the planets meet the requirements, then return an empty string, `""`. Finally, multiple planets can contain all of the required elements; in this case, return the planet that is closest to the maximum possible size.
Example:
```["OHNCCaP_100", "OHC_200", "OCa_50", "OHCCaP_400", "OHNCCaP_225", "OHCa_250"], 250 --> "OHNCCaP_225"```
Note:
* Only elements from 1 to 118 are used, and there are no repeating elements on a planet
**Periodic Table**:
|
reference
|
import re
REQUIRED_ELEMENTS = {'H', 'C', 'N', 'O', 'P', 'Ca'}
def best_planet(solar_system, max_size):
candidates = []
for planet in solar_system:
# Parse the planet
elements, area = planet . split('_', 1)
area = int(area)
if area > max_size:
continue
elements = set(re . findall('[A-Z][a-z]?', elements))
if REQUIRED_ELEMENTS <= elements:
candidates . append((area, planet))
if not candidates:
return ''
candidates . sort()
return candidates[- 1][1]
|
Identify Best Planet
|
6474b8964386b6795c143fd8
|
[
"Strings",
"Algorithms",
"Searching"
] |
https://www.codewars.com/kata/6474b8964386b6795c143fd8
|
6 kyu
|
# Squaredle solver
## Introduction
[Squaredle](https://squaredle.app/) is a game in which players find words by connecting letters up, down, left, right and diagonally. Each square in the puzzle can be used only once.
The purpose of this kata is to simulate a Squaredle player, finding all words in a puzzle.
### Task
Write a function that returns a list of words, containing all words in a Squaredle puzzle.
Words form a letter snake through the puzzle: each letter must be connected up, down, left, right or diagonally to its neighboring letters in the word. It is not allowed to move through missing squares.
Pay attention to the performance of your function.
### Example
```
--- --- ---
| c | d | | This puzzle contains 'code', 'cows', 'owed', 'wars' and 'codes'.
--- --- ---
| o | | e | It doesn't contain 'does' (no moving through missing squares).
--- --- ---
| | w | s | So given 'cd -o e- ws-ar ', your function should return
--- --- ---
| a | r | | ['code', 'cows', 'owed', 'wars', 'codes'].
--- --- ---
```
### Input
A string representation of the puzzle.
* Puzzles are rectangular, but not necessarily square
* Puzzles have ```2 <= r <= 10``` rows and ```2 <= c <= 10``` colums
* Letters are in lower case ```a-z```
* Rows are separated by a hyphen ```-```
* Missing squares are denoted by a space ``` ```
### Output
A list of words.
* Contains all words in the puzzle
* Sorted by length, then alphabetically
* If there are no words in the puzzle, return an empty list
#### Words
All valid words for this kata are preloaded in the list ```WORDS```.
* There are 14,460 valid words
* Words are at least 4 letters
* Words are in lower case
|
games
|
from preloaded import WORDS
from itertools import product
DIRS = set(product(range(- 1, 2), repeat=2)) - {(0, 0)}
class Trie:
def __init__(self):
self . root = {}
def insert(self, word):
cur = self . root
for char in word:
if char not in cur:
cur[char] = {}
cur = cur[char]
cur['#'] = ''
trie = Trie()
for word in WORDS:
trie . insert(word)
def squaredle(puzzle):
def dfs(x, y, snake, t):
if len(snake) > 3 and '#' in t:
res . add(snake)
for dx, dy in DIRS:
i, j = x + dx, y + dy
if N > i >= 0 <= j < M and grid[i][j] != ' ' and not seen[i][j]:
seen[i][j] = 1
char = grid[i][j]
if char in t:
dfs(i, j, snake + char, t[char])
seen[i][j] = 0
res = set()
grid = puzzle . split('-')
N, M = len(grid), len(grid[0])
for i, j in product(range(N), range(M)):
char = grid[i][j]
if char != ' ':
seen = [[0] * M for _ in range(N)]
seen[i][j] = 1
if char in trie . root:
dfs(i, j, char, trie . root[char])
return sorted(res, key=lambda w: (len(w), w))
|
Squaredle solver
|
6495a5ad802ef5000eb70b91
|
[
"Puzzles",
"Games",
"Algorithms",
"Strings"
] |
https://www.codewars.com/kata/6495a5ad802ef5000eb70b91
|
4 kyu
|
Grayscale colors in RGB color model are colors that have the same values for Red, Green and Blue. For example, `#606060` is a grayscale color, while `#FF0055` is not.
In order to correctly convert a color to grayscale, one has to use luminance Y for Red, Green and Blue components. One can calculate luminance Y through the formula introduced in the NTSC standard:
```
Y = 0.299 * R + 0.587 * G + 0.114 * B
```
This formula closely represents the average person's relative perception of the brightness of red, green, and blue light.
Given a color in 6-digit [hexidecimal notation](https://en.wikipedia.org/wiki/Web_colors) `#RRGGBB` in upper case, convert it to grayscale `#YYYYYY`. The answer should be a string representing the color code in 6-digit hexidecimal notation in upper or lower case.
Round the value of luminance Y to the closest integer.
All inputs will be valid.
|
reference
|
def rgb_to_grayscale(color):
""" #Assumes format: #RRGGBB
Multiply and accumulate converted(str_hex->int) RR/GG/BB with corresponding luminance values.
Convert the rounded result back to str_hex and remove the '0x' in front
Add a '#' and use the str_hex result three times.
"""
return '#' + 3 * format(round(0.299 * int(color[1: 3], 16)
+ 0.587 * int(color[3: 5], 16)
+ 0.114 * int(color[5: 7], 16)
),
'02X')
|
Color to Grayscale
|
649c4012aaad69003f1299c1
|
[
"Strings",
"Algorithms"
] |
https://www.codewars.com/kata/649c4012aaad69003f1299c1
|
7 kyu
|
## Prologue:
You get back from work late at night, roaming the streets of Japan (it has to be!). As you are headed home, starved after a long and grueling day at work, stumble upon a ramen shop still serving customers. You dash in, practically drooling for some ramen -- but as soon as you walk in, you realize just how chaotic this restaurant is.
## Problem:
You're standing in a line, where everybody seems to be playing a game for entry. The owner of the restaurant stands at the "front", bringing guests in individually.
There are four "types" of guests:
1. *Known guests* -> Guests who know the restaurant owner personally. These people can enter as they please, without having to wait in a line. Whenever the owner meets a known guest, he yells out "SWAP", requiring everybody to switch places with the person on the "opposite" end of the line, **except for other known guests**
2. *Members* → Guests who have an active membership subscription at the food chain. These people have priority over *unknown guests*, but are not immune to swapping.
3. *Decoys* → These are actually staff members that are hidden into the line, in order to make the game more interesting. When swapping, decoys aren’t allowed to swap, maintaining their position in line. To better disguise themselves, they are given the same priority level as "unknown guests".
4. *Unknown Guests* → The typical person, either too broke to afford a membership, or trying out the restaurant for the first time. They are subject to swaps and get bottom tier priority.
You are given a list of the people that are waiting in queue, each numbered 1-3 except you, who is `0`, and "unknown guests", which can be any other positive number. Your goal is to determine how long it will take for you to get seated (with each person being removed from queue being considered a "minute", including yourself).
## Examples:
```python
queue = [1, 1, 3, 2, 0] # The given queue
sorted = [1, 1, 2, 3, 0] # Sorted by priority
# ^-- you
```
```javascript
queue = [1, 1, 3, 2, 0] // The given queue
sorted = [1, 1, 2, 3, 0] // Sorted by priority
// ^-- you
```
- The 1's are the "known guests", so they get priority.
- The 2's are the "members", so they get secondary priority.
- The resulting array is `[1, 1, 2, 3, 0]`
- The first "known guest" gets consumed, so the swap occurs on the remaining elements in the list `[1, 2, 3, 0]`
- `1` cannot swap with `0`, and `3` cannot swap with `2`
- Repeat, resulting in `[2, 3, 0]`.
- `0` and `2` can be swapped, resulting in `[0, 3, 2]`
- With `0` in front, it took 3 minutes for you to get seated, so the answer is `3`
```python
queue = [0, 8, 2, 1, 4, 2, 12, 3, 2] # The given queue
sorted = [1, 2, 2, 2, 0, 8, 4, 12, 3] # Sorted by priority
# ^-- you
```
```javascript
queue = [0, 8, 2, 1, 4, 2, 12, 3, 2] // The given queue
sorted = [1, 2, 2, 2, 0, 8, 4, 12, 3] // Sorted by priority
// ^-- you
```
- The first "known guest" gets consumed: `[2, 2, 2, 0, 8, 4, 12, 3]`
- `2` cannot swap with `3`
- the rest swap, resulting in: `[2, 12, 4, 8, 0, 2, 2, 3]`
- The numbers up to the `0` get "consumed", as no more swapping is required
- With `0` in front, it took 6 minutes for you to get seated, so the answer is `6`
|
reference
|
from itertools import count
NO_SWAP = (1, 3)
def get_in_line(arr: list[int]) - > int:
arr = [v for v in reversed(arr) if not v or v > 2] + \
[2] * arr . count(2) + [1] * arr . count(1)
for time in count(1):
match arr . pop():
case 1:
for i in range(len(arr) >> 1):
if arr[i] not in NO_SWAP and arr[- i - 1] not in NO_SWAP:
arr[i], arr[- 1 - i] = arr[- i - 1], arr[i]
case 0:
return time
case _:
return time + len(arr) - arr . index(0)
|
LET ME IN!
|
6498aa0daff4420024ce2c88
|
[
"Fundamentals",
"Performance"
] |
https://www.codewars.com/kata/6498aa0daff4420024ce2c88
|
6 kyu
|
### Subsequences:
[Subsequence](https://en.wikipedia.org/wiki/Subsequence) for the Kata is defined as following:
__For a collection of numbers, a subsequence is one of the possible results you can get by removing some of the numbers from the collection, keep the original order.__
```
Example: [1, 3, 5]
All subsequences are:
[] (Remove all numbers)
[1] (Remove 3, 5)
[3] (Remove 1, 5)
[5] (Remove 1, 3)
[1, 3] (Remove 5)
[1, 5] (Remove 3)
[3, 5] (Remove 1)
[1, 3, 5] (Keep all)
```
___
### No Adjacent Items:
Now we look at all the subsequences, check if there are numbers which are adjacent to each other in the original collection.
In the above example:
```
[1, 3] (1, 3) => adjacent items
[3, 5] (3, 5) => adjacent items
[1, 3, 5] (1, 3) and (3, 5) => adjacent items
```
And we only want no adjacent items:
```
[1, 3, 5] => [[], [1], [3], [5], [1, 5]]
```
___
### Task:
* You will get a list of numbers, as input, it will have no repeated numbers.
* Return all subsequences with no adjacent items, your answer will be sorted, so the order does not matter.
___
### Performance:
```
1 <= size of input list <= 25
When the size is 25:
1. Total amount of subsequences is 33554432
2. Total amount of subsequences with no adjacent items is 196418
```
* 70 tests with input size <= `9`
* 25 tests with input size <= `20`
* for input size from `21` to `25`, 1 test for each
___
### Examples:
__input => output__
```
[0] => [[], [0]]
[2, 1] => [[], [1], [2]]
[1, 3, 5] => [[], [1], [1, 5], [3], [5]]
[8, 2, 6, 4] => [[], [2], [2, 4], [4], [6], [8], [8, 4], [8, 6]]
```
|
algorithms
|
def no_adjacent_subsequences(lst):
xs, ys = [[]], [[]]
for v in lst:
xs, ys = ys, ys + [x + [v] for x in xs]
return ys
|
Subsequences with no adjacent items
|
6493682fbefb70000fc0bdff
|
[
"Algorithms",
"Performance"
] |
https://www.codewars.com/kata/6493682fbefb70000fc0bdff
|
6 kyu
|
# Description
Below is described a skill tree:
<!-- commented out this cool css tree since codewars broke css rendering -->
<!-- <html>
<body>
<style>
<!-- credit to codepen.io/Gerim :) >
.body { }
.tree ul {
margin: 0;
padding: 0;
padding-top: 20px;
position: relative;
transition: all 0.5s;
-webkit-transition: all 0.5s;
-moz-transition: all 0.5s;
}
.tree li {
float: left;
text-align: center;
list-style-type: none;
position: relative;
padding: 20px 5px 0 5px;
transition: all 0.5s;
-webkit-transition: all 0.5s;
-moz-transition: all 0.5s;
}
.tree li::before,
.tree li::after {
content: '';
position: absolute;
top: 0;
right: 50%;
border-top: 1px solid #ccc;
width: 50%;
height: 20px;
}
.tree li::after {
right: auto;
left: 50%;
border-left: 1px solid #ccc;
}
.tree li:only-child::after,
.tree li:only-child::before {
display: none;
}
.tree li:only-child {
padding-top: 0;
}
.tree li:first-child::before,
.tree li:last-child::after {
border: 0 none;
}
.tree li:last-child::before {
border-right: 1px solid #ccc;
border-radius: 0 5px 0 0;
-webkit-border-radius: 0 5px 0 0;
-moz-border-radius: 0 5px 0 0;
}
.tree li:first-child::after {
border-radius: 5px 0 0 0;
-webkit-border-radius: 5px 0 0 0;
-moz-border-radius: 5px 0 0 0;
}
.tree ul ul::before {
content: '';
position: absolute;
top: 0;
left: 50%;
border-left: 1px solid #ccc;
width: 0;
height: 20px;
}
.tree li a {
border: 1px solid #ccc;
padding: 5px 10px;
text-decoration: none;
color: #ff0000;
font-family: Arial, Verdana, Tahoma;
font-size: 11px;
display: inline-block;
border-radius: 5px;
-webkit-border-radius: 5px;
-moz-border-radius: 5px;
transition: all 0.5s;
-webkit-transition: all 0.5s;
-moz-transition: all 0.5s;
}
.tree li a:hover,
.tree li a:hover+ul li a {
background: #c8e4f8;
color: #000;
border: 1px solid #94a0b4;
}
.tree li a:hover+ul li::after,
.tree li a:hover+ul li::before,
.tree li a:hover+ul::before,
.tree li a:hover+ul ul::before {
border-color: #94a0b4;
}
</style>
<div class="tree">
<ul>
<li>
<a>0</a>
<ul>
<li>
<a>1</a>
<ul>
<li>
<a>3</a>
<ul>
<li>
<a>4</a>
</li>
<li>
<a>5</a>
</li>
</ul>
</li>
</ul>
</li>
<li>
<a>2</a>
<ul>
<li>
<a>6</a>
</li>
</ul>
</li>
</ul>
</li>
</ul>
</div>
</body>
</html>
<br><br><br><br><br><br><br><br><br><br><br> -->
<img alt="Tree" src="https://gist.githubusercontent.com/el-f/387770bf21b35add9a694c829b7df855/raw/b2c8c551177d3220f48c58ada2e1902462c1206e/tree.svg" style="max-width: 480px;">
The array that describes this skill tree is as follows:
```python
[
0, # 0 is the root and does not depend on any skill.
0, # 1 is unlocked by skill 0 (skill at index 0).
0, # 2 is unlocked by skill 0.
1, # 3 is unlocked by skill 1.
3, # 4 is unlocked by skill 3.
3, # 5 is unlocked by skill 3.
2 # 6 is unlocked by skill 2.
]
```
In another words, each skill is identified by its index in the array, and its value identifies the skill that unlocks it.
---
# Your Task:
Given a skill tree described as an array and a set of required skills, return the total number of skills needed to learn all of the required skills.
<b>Intuition</b>: In the example's tree, if I want to learn skill 6, I first need to learn skills 0 and 2 - a total of 3 skills learned.
---
# Examples:
```python
count_skills([ 0, 0, 0, 1, 3, 3, 2 ], { 6 }) -> 3
count_skills([ 0, 0, 0, 1, 3, 3, 2 ], set()) -> 0
count_skills([ 0, 0, 0, 1, 3, 3, 2 ], { 1, 2 }) -> 3
```
```scala
countSkills(Seq( 0, 0, 0, 1, 3, 3, 2 ), Set( 6 )) -> 3
countSkills(Seq( 0, 0, 0, 1, 3, 3, 2 ), Set[Int]()) -> 0
countSkills(Seq( 0, 0, 0, 1, 3, 3, 2 ), Set( 1, 2 )) -> 3
```
```javascript
countSkills([ 0, 0, 0, 1, 3, 3, 2 ], new Set([ 6 ])); -> 3
countSkills([ 0, 0, 0, 1, 3, 3, 2 ], new Set()); -> 0
countSkills([ 0, 0, 0, 1, 3, 3, 2 ], new Set([ 1, 2 ])); -> 3
```
```rust
countSkills(&[0, 0, 0, 1, 3, 3, 2], &HashSet::from([6])) -> 3
countSkills(&[0, 0, 0, 1, 3, 3, 2], &HashSet::new()) -> 0
countSkills(&[0, 0, 0, 1, 3, 3, 2], &HashSet::from([1, 2])) -> 3
```
```java
countSkills(new int[] { 0, 0, 0, 1, 3, 3, 2 }, Set.of( 6 )); -> 3
countSkills(new int[] { 0, 0, 0, 1, 3, 3, 2 }, Set.of()); -> 0
countSkills(new int[] { 0, 0, 0, 1, 3, 3, 2 }, Set.of( 1, 2 )); -> 3
```
---
## Constraints:
- <b>Each skill is only unlocked by exactly one skill!</b>
- Skills can unlock any number of skills.
- Inputs are always valid and each skill can be unlocked by some other skill, except 0.
~~~if-not:rust,java
- `$0 \le len(tree) \le 200\,000$`
~~~
~~~if:rust,java
- `$0 \le len(tree) \le 300\,000$`
~~~
- `$0 \le len(required) \le len(tree)$`
---
## Notes:
- You need to be somewhat efficient with your approach.
- You are provided with 2 functions in `preloaded` to help you debug:
1. `build_tree/buildTree` - convert a tree array into a dict/Map describing which skills each skill unlocks.
2. `visualize_tree/visualiseTree/visualizeTree` - get a visual representation of the given tree array.
|
algorithms
|
def count_skills(tree, required):
skils = set()
for r in required:
while r not in skils:
skils . add(r)
r = tree[r]
return len(skils)
|
Skills Master
|
648f2033d52f51608e06c458
|
[
"Algorithms",
"Data Structures",
"Graph Theory",
"Trees"
] |
https://www.codewars.com/kata/648f2033d52f51608e06c458
|
6 kyu
|
_This Kata is intended to be a simple version of [Binary with unknown bits: average to binary](https://www.codewars.com/kata/6440554ac7a094000f0a4837)._
_The main difference is that in this Kata, input `n` will only be an __integer__, and only consider those binary string with exactly __one__ `x` (or cases of 0 and 1)._
_After work out the __pattern__ for this Kata, you can try to work out the pattern for 2 or more `x`s, also the cases of __integer + 0.5__ for the above linked Kata._
_There are many different approaches other than this one for the other Kata._
___
### Background
In [another Kata](https://www.codewars.com/kata/64348795d4d3ea00196f5e76) you calculated the `average number` from a string of binary with unknown bits, using the rules (see rules section below).
We now define `average` as the result calculated in the way described in that Kata.
___
### Average to Binary
You need the original binary strings, but somebody deleted them, there is no way to get them back.
The only solution is to use the average `n` to find the original binary strings.
Also, we know that the orginal binary strings has exactly one `x` in it.
It looks like this:
```
average => string
4 => 'x00'
5 => '1x0'
5 => 'x01'
```
But some numbers will result in more than one strings.
So we collect all strings for the input into a __set__.
It looks like this:
```
average => set of strings
4 => {'x00'}
5 => {'1x0', 'x01'}
```
And the task of this Kata is to write the function which takes the number `n` and returns the set.
___
### Task:
* You will get a non-negative __integer__ `n` as input.
* Find all the strings with exactly one `x` in it: for each string, its `average` would equal to the input `n`.
* Return a set of all strings found.
___
### Rules:
1. The string consists of `0`, `1` and/or `x`, if its length is 2 or higher, it would have exactly one `x`.
2. Unless the number is a single zero(`0`), otherwise no leading zeros are allowed.
3. `x` can be 0 or 1, but the string has to follow the above rules.
___
### Performance
* `small tests`: 30 tests of numbers up to _2^20_
* `Med Tests`: 30 tests of numbers up to _2^30_
* `BIG TESTS`: 30 tests of numbers up to _2^40_
* `*E*X*T*R*A* *T*E*S*T*S*`: 10 tests of numbers up to _2^50_
___
### Example
```
Input n = 25
25 => average of 25 => '11001' => 'x1001'
24:'11000'
25 => average of 24 and 26 => 26:'11010' => '110x0'
result > '110x0'
21:'10101'
25 => average of 21 and 29 => 29:'11101' => '1x101'
result > '1x101'
The set of 25 is {'110x0', '1x101', 'x1001'}.
```
___
### Sample Tests
```
0 => {'0'}
1 => {'1'}
2 => {'x0'}
3 => {'x1'}
4 => {'x00'}
5 => {'1x0', 'x01'}
6 => {'1x1', 'x10'}
25 => {'110x0', '1x101', 'x1001'}
1572864 => {'x10000000000000000000', '1x1000000000000000000'}
```
###### Don't ask what happened to the guy who deleted the original strings, it is a horrible story.
|
games
|
def average_to_binary(n):
res, ln = {'x' + f' { n : b } ' [1:]
} if n > 1 else {f' { n } '}, len(f' { n : b } ')
for k in range(ln - 2):
cand = f' { n - 2 * * k : b } '
if cand[- k - 2] == '0':
res . add(cand[: - k - 2] + 'x' + cand[- k - 1:])
return res
|
Binary with an unknown bit: average to binary (Simple Version)
|
6484e0e4fdf80be241d85878
|
[
"Binary",
"Strings",
"Performance",
"Mathematics"
] |
https://www.codewars.com/kata/6484e0e4fdf80be241d85878
|
6 kyu
|
In [another Kata](https://www.codewars.com/kata/64348795d4d3ea00196f5e76) you calculated the `average number` from a string of binary with unknown bits, using the rules (see rules section below).
We now define `average` as the result calculated in the way described in that Kata.
___
### Average to Binary
You need the original binary strings, but somebody deleted them, there is no way to get them back.
The only solution is to use the average `n` to find the original binary strings.
It looks like this:
```
average => string
0.5 => 'x'
1.5 => (no such a string)
2.5 => 'xx'
2.5 => '1x'
```
But some numbers will result in more than one string, or no string.
So we collect all strings for the input into a list.
It looks like this:
```
average => list of strings
0.5 => ['x']
1.5 => []
2.5 => ['1x', 'xx']
```
And the task of this Kata is to write the function which take the number `n` and return the list.
___
### Task:
* You will get a non-negative number `n` as input. It would be an __integer__ or __integer plus 0.5__.
* Find all strings: for each string, its `average` would equal to the input `n`.
* Return a list of all strings found. If nothing found, return an empty list. The order of the list does not matter.
___
### Rules:
1. The string consists of `0`, `1` and/or `x`, if its length is 2 or higher, it would have at least one `x`.
2. Unless the number is a single zero(`0`), otherwise no leading zeros are allowed.
3. `x` can be 0 or 1, but the string has to follow the above rules.
___
### Performance:
The input number would be less than _2^31_.
___
### Examples:
Here are some examples:
```
Example no.1:
n = 0.5
0.5 => average of 0, 1
convert to binary => '0', '1'
binary with unknown bits => 'x'
list of strings => ['x']
_____
Example no.2:
n = 2.5
2.5 => average of 2, 3
convert to binary => '10', '11'
binary with unknown bits => '1x', 'xx'
list of strings => ['1x', 'xx']
_____
Example no.3:
n = 5
5 => average of 4, 6
convert to binary => '100', '110'
binary with unknown bits => '1x0', 'xx0'
5 => average of 5
convert to binary => '101'
binary with unknown bits => 'x01'
('101' has 3 bits but no 'x' in it, violated the rule)
list of strings => ['1x0', 'x01', 'xx0']
```
other sample tests:
```
0 => ['0']
1 => ['1']
1.5 => []
2 => ['x0']
5.5 => ['1xx', 'xxx']
10 => ['10x1', '1x00', 'x010', 'x0x1', 'xx00']
10.5 => ['101x', '1x0x', 'x01x', 'xx0x']
21 => ['101x0', '10x11', '1x001', '1x0x0', 'x0101', 'x01x0', 'x0x11', 'xx001', 'xx0x0']
21.5 => ['101xx', '1x0xx', 'x01xx', 'xx0xx']
23.5 => ['1xxxx', 'xxxxx']
2050 => ['1000000000x1', '100000000x00', 'x00000000010', 'x000000000x1', 'x00000000x00']
```
___
### hint:
Some hints might help?
1. Solve the kata linked at the top might help.
2. There are some special cases other than cases `0`, `0.5` and `1`.
3. Try to convert the input n to binary.
___
###### Don't ask what happened to the guy who deleted the original strings, it is a horrible story.
|
games
|
from functools import cache
from itertools import chain
@ cache
def f(n):
match n:
case 0.5: return []
case 0: return ['']
case 1: return ['1', 'x']
match n % 1:
case 0.5: return [s + 'x' for s in f((n - 0.5) / 2)]
case 0: return [* chain([s + 'x' for s in f((n - 0.5) / 2)],
[s + '0' for s in f(n / 2)],
[s + '1' for s in f((n - 1) / 2)])]
case _: return []
def average_to_binary(n):
match n:
case 0: return ['0']
case 0.5: return ['x']
case 1: return ['1']
return [s for s in f(n) if 'x' in s]
|
Binary with unknown bits: average to binary
|
6440554ac7a094000f0a4837
|
[
"Mathematics",
"Binary",
"Performance",
"Strings",
"Puzzles"
] |
https://www.codewars.com/kata/6440554ac7a094000f0a4837
|
4 kyu
|
### Task
If possible, divide the integers 1,2,…,n into two sets of equal sum.
### Input
A positive integer n <= 1,000,000.
### Output
If it's not possible, return [ ] (Python, Javascript, Swift, Ruby) or ( ) (Python) or [ [],[] ] (Java, C#, Kotlin) or None (Scala). <br>
If it's possible, return two disjoint sets. Each integer from 1 to n must be in one of them. The integers in the first set must sum up to the same value as the integers in the second set. The sets can be returned in a tuple, list, or array, depending on language.
### Examples:
For n = 8, valid answers include:<br>
[1, 3, 6, 8], [2, 4, 5, 7] (or [[1, 3, 6, 8], [2, 4, 5, 7]])<br>
[8, 1, 3, 2, 4], [5, 7, 6] <br>
[7, 8, 3], [6, 1, 5, 4, 2], and others.
For n = 9 it is not possible. For example, try [6, 8, 9] and [1, 2, 3, 4, 5, 7], but the first sums to 23 and the second to 22. No other sets work either.
Source: [CSES](https://cses.fi/problemset/task/1092)
|
games
|
def create_two_sets_of_equal_sum(n):
if n % 4 in {1, 2}:
return []
return [[* range(1, n / / 4 + 1), * range(n * 3 / / 4 + 1, n + 1)], [* range(n / / 4 + 1, n * 3 / / 4 + 1)]]
|
Two Sets of Equal Sum
|
647518391e258e80eedf6e06
|
[
"Arrays",
"Algorithms"
] |
https://www.codewars.com/kata/647518391e258e80eedf6e06
|
6 kyu
|
## Problem Statement
*This kata is an easier version of [this kata](https://www.codewars.com/kata/60228a9f85a02c0022379542). If you like this kata, feel free to try the harder version.*
You are given the outcomes of a repeated experiment in the form of a list of zeroes and ones, e.g. `[1, 0, 0, 1, 1]`, where `0` means that the experiment failed and `1` means that it was successful. The list is ordered by the time the experiments where performed such that the outcome of the last performed experiment is last in the list.
Your task is to present the result of the experiments in the best light possible. In particular, you should find the **longest contiguous subsequence** having the highest success rate, i.e. the maximum average value. (The subsequence must obviously be contiguous, otherwise we could just cherry pick all the successful experiments.) Moreover, the subsequence should have a length greater than or equal to some specified value `k`, because it would not be that impressive to have a success rate of `1.0` when you only look at one or a few experiments.
Given a positive integer `k` and a list `arr` of `0's` and `1's`, e.g. `arr = [1, 0, 0, 1, 1]` , find the **index** of the start of the longest contiguous subsequence with the highest average value and length `>= k`. Also find the **length** of this subsequence. Return the answer as a **tuple** `(index, length)`.
If there are multiple contiguous subsequences with maximal length and average value, choose the one that comes last in the list, since this represents the most recent sequence of experiments.
## Example
Consider the case:
```python
Input: arr = [0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1], k = 3
```
With `k = 3` subarray has to be of length *at least* `3`. The highest possible average value is then `2/3`, and there are seven subarrays with this average value:
```python
[0, 1, 1], [1, 1, 0], [1, 1, 0, 0, 1, 1], [0, 1, 1], [1, 1, 0], [1, 1, 0, 0, 1, 1], [0, 1, 1]
^ ^ ^ ^ ^ ^ ^
index: 0 1 1 4 5 5 8
```
Two of these subarrays have the maximal length `6`, the first starting from index `i = 1`, and the other starting from `i = 5`:
```python
[1, 1, 0, 0, 1, 1]
v v
[0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1]
^ ^
[1, 1, 0, 0, 1, 1],
```
The largest starting index should be chosen so the result is `i = 5` and `length = 6`, which should be returned as a tuple.
```python
Output should be: (5, 6)
```
## Input/Output
**Input**: a list `arr` of integers `0` and `1`, with a size `n <= 1,000`, and a positive integer `1 <= k <= 200`.
**Output**: a tuple `(i, l)` where `i` is the index where the subarray starts and `l`, `l >= k`, is the length of the subarray.
If `k` is greater than the size of the input list or if the input list is empty, return an empty tuple `()`. See the sample tests for more examples.
### Expected time complexity: O( n<sup>2</sup> )
|
reference
|
def solve(arr, k):
max_mean = 0
tapir = ()
for i in range(len(arr) - k + 1):
sum_slice = 0
for j in range(len(arr)):
sum_slice += arr[j]
if j + 1 >= k + i:
if sum_slice / (k + i) >= max_mean:
max_mean = sum_slice / (k + i)
tapir = (j - (k + i - 1), k + i)
sum_slice -= arr[j - (k + i - 1)]
return tapir
|
Longest Subarray with Maximum Average Value
|
60983b03bdfe880040c531d6
|
[
"Algorithms",
"Fundamentals"
] |
https://www.codewars.com/kata/60983b03bdfe880040c531d6
|
5 kyu
|
Consider the process of stepping from integer x to integer y. The length of each step must be a positive integer, and must be either one bigger, or equal to, or one smaller than, the length of the previous step. The length of the first and last steps must be 1.
Create a function that computes the minimum number of steps needed to go from x to y. It should handle 0 <= x <= y < 2<sup>31</sup>.
Source: Problem 6.6.8 from Skiena & Revilla, "Programming Challenges".
Examples:
x = 45, y = 48: Clearly the steps are 46,47,48, so the result is 3.
x = 45, y = 49: We can take one 2-step: 46,48,49, so the result is still 3.
x = 45, y = 50: Still one 2-step: 46,48,49,50, so the result is 4.
x = 45, y = 51: Two 2-steps: 46,48,50,51, so the result remains 4.
And so on.
Having the function consider the different possibilities in this way is not practical for large values. What characterizes these optimal sequences of steps? The example tests might help.
You might also enjoy [Shortest steps to a number](https://www.codewars.com/kata/5cd4aec6abc7260028dcd942). It looks somewhat similar (maybe)!
|
games
|
def step(x, y):
return int((4 * (y - x) - (y > x)) * * .5)
|
Steps
|
6473603854720900496e1c82
|
[
"Puzzles",
"Mathematics",
"Combinatorics"
] |
https://www.codewars.com/kata/6473603854720900496e1c82
|
7 kyu
|
### Background
Pat Programmer is worried about the future of jobs in programming because of the advance of AI tools like ChatGPT, and he decides to become a chef instead! So he wants to be an expert at flipping pancakes.
A pancake is characterized by its diameter, a positive integer.
Given a stack of pancakes, you can insert a spatula under any pancake and then flip, which reverses the order of all the pancakes on top of the spatula.
### Task
Write a function that takes a stack of pancakes and returns a sequence of flips that arranges them in order by diameter, with the largest pancake at the bottom and the smallest at the top. The pancakes are given as a list of positive integers, with the left end of the list being the top of the stack.
Based on Problem 4.6.2 in Skiena & Revilla, "Programming Challenges".
### Example
Consider the stack [1,5,8,3]. One way of achieving the desired order is as follows:
The 8 is the biggest, so it should be at the bottom. Put the spatula under it (position 2 in the list) and flip. <br>
This transforms the stack into [8,5,1,3], with the 8 at the top. Then flip the entire stack (spatula position 3). <br>
This transforms the stack into [3,1,5,8], which has the 8 at the bottom.
And since the 5 is in the correct position as well, now flip the 1 and 3 (spatula position 1). <br>
The stack is now [1,3,5,8], as desired. The function should return [2,3,1].
### Note
You don't have to find the shortest sequence of flips. That is a hard problem - see https://en.wikipedia.org/wiki/Pancake_sorting. However, don't include unnecessary flips, in the following sense:
(1) If 2 consecutive flips leave the stack in the same state, they should be omitted.
For example, [2,3,2,2,1] also arranges [1,5,8,3] correctly, but 2,2 is unnecessary. <br>
(2) Flipping only the top pancake doesn't achieve anything.
Performance should not be a issue. If Pat can flip 1,000 pancakes with diameters between 1 and 1,000, he thinks he can get a job!
|
reference
|
def flip_pancakes(stack):
tp, st, res = len(stack) - 1, stack[:], []
while tp > 0:
if st[tp] != max(st[: tp + 1]):
ind = max(range(tp + 1), key=lambda k: st[k])
st = st[ind + 1: tp + 1][:: - 1] + st[: ind + 1] + st[tp + 1:]
res . extend([ind] * (ind > 0) + [tp])
tp -= 1
return res
|
Flip Your Stack (of Pancakes)
|
6472390e0d0bb1001d963536
|
[
"Arrays",
"Sorting"
] |
https://www.codewars.com/kata/6472390e0d0bb1001d963536
|
6 kyu
|
A Euler square (also called a Graeco-Latin square) is a pair of orthogonal latin squares. A latin square is an n × n array filled with the integers 1 to n each occurring once in each row and column - see [Latin Squares](https://www.codewars.com/kata/645fb55ecf8c290031b779ef). Two latin squares are orthogonal if each *r* between 1 and n in the 1st square is paired (i.e. occurs at the same position) exactly once with each *s* between 1 and n in the 2nd square.
Example of size 3:
```
[[3,1,2], [[3,2,1],
[2,3,1], [2,1,3],
[1,2,3]], [1,3,2]]
```
Explanation:<br>1 in the 1st square is paired with 2 in the first row of the 2nd square, with 3 in the second row, and with 1 in the third row.<br>
2 in the 1st square is paired in the 2nd square with 1 in the first row, 2 in the second row, and 3 in the third row.<br>
And 3 is paired with 3 in the first row, 1 in the second row, and 2 in the third row.
If the 2nd square was a duplicate of the 1st, they would not be orthogonal, because each integer would be paired with itself three times.
Example of size 5:
```
[[5, 2, 4, 1, 3], [[5, 1, 2, 3, 4],
[4, 1, 3, 5, 2], [4, 5, 1, 2, 3],
[3, 5, 2, 4, 1], [3, 4, 5, 1, 2],
[2, 4, 1, 3, 5], [2, 3, 4, 5, 1],
[1, 3, 5, 2, 4]] [1, 2, 3, 4, 5]]
```
1 in the 1st square is paired in successive rows of the 2nd square with 3, 5, 2, 4, 1. The reader is invited to verify that 2,3,4 and 5 in the 1st square are also paired with 1-5 in some order in the 2nd square.
Task: Write a function that creates a Euler square for any **odd** positive integer n. Your function will be tested for odd n < 200.
It turns out doing this for even n is much harder. This might be the subject of a future kata.
("Really? I don't think so". "Why not"? "Do you understand how to do it?" "Uh, no. I thought you did". "Definitely not. Even Euler didn't!")
See the section "Euler's conjecture and disproof" at https://en.wikipedia.org/wiki/Mutually_orthogonal_Latin_squares#Graeco-Latin_squares".
|
games
|
def create_euler_square(n): # Assume n is odd.
return [[(i + j) % n + 1 for j in range(n)] for i in range(n)], \
[[(2 * i + j) % n + 1 for j in range(n)] for i in range(n)]
|
Euler Squares
|
6470e15f4f0b26052c6151cd
|
[
"Algorithms",
"Arrays"
] |
https://www.codewars.com/kata/6470e15f4f0b26052c6151cd
|
6 kyu
|
# Task
Write a function which when given a non-negative integer `n` and an arbitrary base `b`, returns the number reversed in that base.
# Examples
- `n=12` and `b=2` return 3, because 12 in binary is "1100", which reverses to "0011", equivalent to 3 in decimal.
- `n=10` and `b=5` return 2, because 10 in base-5 is "20", which reverses to "02", equivalent to 2 in decimal.
- `n=45` and `b=30` return 451, because 45 in base-30 is "1F", which reverses to "F1", equivalent to 451 in decimal.
- `n=3` and `b=4` return 3, because 3 in base-4 is "3", which reverses to "3", equivalent to 3 in decimal.
- `n=5` and `b=1` return 5, because 5 in unary is "|||||", which reverses to "|||||", equivalent to 5 in decimal.
# Note
- The function should return an integer.
- The base `b` will be greater or equal to 1.
- Edge case: Base-1 is also used in this kata to represent the [unary numeral system](https://en.wikipedia.org/wiki/Unary_numeral_system). Think of it as a system of tally marks. For example:
* `3` (decimal) -> `|||` (unary)
* `5` (decimal) -> `|||||` (unary)
|
algorithms
|
def reverse_number(n, b):
if b == 1:
return n
m = 0
while n:
n, r = divmod(n, b)
m = m * b + r
return m
|
Reverse a number in any base
|
6469e4c905eaefffd44b6504
|
[
"Algorithms"
] |
https://www.codewars.com/kata/6469e4c905eaefffd44b6504
|
7 kyu
|
### Background
A **latin square** is an n × n array filled with the integers 1 to n, each occurring once in each row and column.
Here are examples of latin squares of size 4 and 7:
```
[[1, 4, 3, 2], [[2, 3, 1, 7, 4, 6, 5],
[4, 3, 2, 1], [7, 1, 6, 5, 2, 4, 3],
[3, 2, 1, 4], [6, 7, 5, 4, 1, 3, 2],
[2, 1, 4, 3]] [4, 5, 3, 2, 6, 1, 7],
[5, 6, 4, 3, 7, 2, 1],
[1, 2, 7, 6, 3, 5, 4],
[3, 4, 2, 1, 5, 7, 6]]
```
Latin squares have many practical uses, for example in error-correcting-codes and the design of agricultural experiments. See https://en.wikipedia.org/wiki/Latin_square for more details. Sudoku is a 9 x 9 latin square, with additional conditions.
Creating a latin square of any size is fairly straightforward (see [Latin Squares](https://www.codewars.com/kata/645fb55ecf8c290031b779ef)). Validating that an arbitrary array is a latin square is slightly trickier, especially if you want to provide helpful feedback messages in case it's not.
### Task
Write a function that validates if an input array is a latin square. It has two parameters, the array and a positive integer *m* > 1. To help the user with debugging, it should return an appropriate message, as detailed below. It must not modify the input array.
### Details
The input array is guaranteed to be 2D and contain only integers. If it is a valid latin square of size *m*, the function should return *"Valid latin square of size <m>"*. Otherwise, it should return one of the following messages:
(1) If the input array is not square, the function should return *"Array not square"*.
(2) If the input array is square, but not of size *m*, the function should return *"Array is wrong size"*. NOTE: When the array is *both* not square and the wrong size, (1) applies, so *"Array not square"* should be returned.
(3) If any value between 1 and *m* in the array occurs more than once in a particular <u>row</u>, the function should identify it and its row by returning "*<value> occurs more than once in row <s>*". If there are multiple such values, only one should be identified. Row indexes run from 1 to *m*.
(4) If any value between 1 and *m* in the array occurs more than once in a particular <u>column</u>, the function should return *"<value> occurs more than once in column <t>*". If there are multiple such values, only one should be identified. Column indexes run from 1 to *m*.
(5) If any value in the array is not between 1 and *m*, the function should identify it and its location by returning *"<value> at <row,col> is not between 1 and <m>*". If there are multiple such values, only one should be identified.
If more than one of the above conditions occur, the function should return **one** of the appropriate messages. For example, suppose *m* is 4 and the array is
```
[[1, 2, 1, 1],
[5, 2, 3, 4],
[4, 3, 0, 2, 1],
[2, 1, 4, 3]].
```
Then the function can return any of the following:
"Array not square"
"1 occurs more than once in row 1"
"2 occurs more than once in column 2"
"5 at 2,1 is not between 1 and 4"
"0 at 3,3 is not between 1 and 4"
#### Worth Noting
There is no known easily-computable formula for the number of latin squares of a given size (see https://en.wikipedia.org/wiki/Latin_square - Number of n × n Latin squares).
If you like this kata, you might also be interested in [Sudokuboard validator](https://www.codewars.com/kata/63d1bac72de941033dbf87ae).
|
algorithms
|
def verify_latin_square(array, m):
def validate():
if not is_square(array):
return "Array not square"
if not is_correct_size(array, m):
return "Array is wrong size"
value_error = fail_not_correct_values()
if value_error:
return value_error
return f"Valid latin square of size { m } "
def fail_not_correct_values():
for i, row in enumerate(array):
for j, value in enumerate(row):
if not is_within_range(value, m):
return f" { value } at { i + 1 } , { j + 1 } is not between 1 and { m } "
if value_occurs_more_than_once(value, row):
return f" { value } occurs more than once in row { i + 1 } "
for j in range(m):
column = [row[j] for row in array]
if len(set(column)) != m:
repeating_value = find_repeating_value(column)
return f" { repeating_value } occurs more than once in column { j + 1 } "
def is_square(array):
return all(len(row) == len(array) for row in array)
def is_correct_size(array, m):
return len(array) == m
def is_within_range(value, m):
return 1 <= value <= m
def value_occurs_more_than_once(value, row):
return row . count(value) > 1
def find_repeating_value(lst):
seen = set()
for value in lst:
if value in seen:
return value
seen . add(value)
def value_occurs_more_than_once_in_column(column, m):
for value in range(1, m + 1):
if column . count(value) > 1:
return value
return validate()
|
Latin Square Validator
|
646254375cee7a000ffaa404
|
[
"Strings",
"Arrays"
] |
https://www.codewars.com/kata/646254375cee7a000ffaa404
|
6 kyu
|
# Background
Most numbers contain the digit `1`; some do not. The percentage of integers below `10^7` (ten million) containing the digit `1` is already 53%! As we consider larger and larger numbers, the percentage of integers containing the digit `1` tends towards 100%.
# Problem Description
In this kata, you are required to build a function that receives a positive integer argument, `n`, and returns the n-th positive integer containing the digit `1`, the first of which is `1`.
* The following numbers contain the digit 1: `10`, `21`, `1024`, `1111111`.
* The following numbers __do not__ contain the digit 1: `42`, `666`, `2048`, `234567890`.
The first 10 integers containing the digit 1 are `1`, `10`, `11`, `12`, `13`, `14`, `15`, `16`, `17` and `18`.
# Input Constraints
* Fixed test cases: `1` ≤ `n` ≤ `100` (one hundred)
* Small test cases: `1` ≤ `n` ≤ `10^5` (one hundred thousand)
* Medium test cases: `1` ≤ `n` ≤ `10^10` (ten billion)
* Large test cases: `1` ≤ `n` ≤ `10^15` (one quadrillion)
`BigInt` is __not__ required in JavaScript.
|
algorithms
|
def nth_num_containing_ones(n, digit=1, base=10):
assert 0 < digit < base
n, a, nth = n - 1, [0], 0
while n >= a[- 1]:
a . append((base - 1) * a[- 1] + base * * (len(a) - 1))
a . pop()
while a:
x = a . pop()
l = base * * len(a)
if 0 <= n - digit * x < l:
nth = (base * nth + digit) * l + n - digit * x
return nth
if n >= l + digit * x:
n -= l - x
d, n = divmod(n, x)
nth = base * nth + d
return nth
|
N-th Integer Containing the Digit 1
|
64623e0ad3560e0decaeac26
|
[
"Number Theory",
"Performance",
"Mathematics"
] |
https://www.codewars.com/kata/64623e0ad3560e0decaeac26
|
4 kyu
|
A **latin square** is an n × n array filled with the integers 1 to n, each occurring once in each row and column.
Here are examples of latin squares of size 4 and 7:
```
[[1, 4, 3, 2], [[2, 3, 1, 7, 4, 6, 5],
[4, 3, 2, 1], [7, 1, 6, 5, 2, 4, 3],
[3, 2, 1, 4], [6, 7, 5, 4, 1, 3, 2],
[2, 1, 4, 3]] [4, 5, 3, 2, 6, 1, 7],
[5, 6, 4, 3, 7, 2, 1],
[1, 2, 7, 6, 3, 5, 4],
[3, 4, 2, 1, 5, 7, 6]]
```
Latin squares have many practical uses, for example in error-correcting-codes and the design of agricultural experiments. See https://en.wikipedia.org/wiki/Latin_square for more details. Sudoku is a special type of 9 x 9 latin square, with additional conditions.
Task: Write a function that returns a latin square for any positive integer n.
You might also enjoy [Latin Square Validator](https://www.codewars.com/kata/646254375cee7a000ffaa404) and [Euler Squares](https://www.codewars.com/kata/6470e15f4f0b26052c6151cd).
|
algorithms
|
def make_latin_square(n):
return [[(i + j) % n + 1 for i in range(n)] for j in range(n)]
|
Latin Squares
|
645fb55ecf8c290031b779ef
|
[
"Arrays"
] |
https://www.codewars.com/kata/645fb55ecf8c290031b779ef
|
7 kyu
|
Given a train track with some trains on it, then the same train track after some time has passed, return True if the arrangement is valid, otherwise return False.
For example, this is valid:
```
before: ">....."
after: ".....>"
```
In this example, a train is facing right. In the `before` time, it is at the beginning of the track. Then by the `after` time, it has traveled to the end of the track.
Input format:
- Input shall consist of a string containing 3 characters:
- `>` indicates a train traveling right
- `<` indicates a train traveling left
- `.` indicates a space - a stretch of empty track.
Requirements:
- trains cannot change direction
- ```
before: "..>.."
after: "..<.."
```
- trains cannot go backward
- ```
before: "..>.."
after: ">...."
```
- train track cannot change length
- ```
before: "..>.."
after: "........>"
```
- trains cannot be created or destroyed
- ```
before: "..>.."
after: "..>>.."
```
- trains cannot enter or leave the given section of train track
- ```
before: "..>.."
after: "....."
```
- trains cannot go past one another
- ```
before: "..><.."
after: "<....>"
```
Performance expectation:
- Solution should work for strings of upto 30k characters.
FAQ:
- Can we have longer trains?
- No, not really. Doesn't make a difference for this problem. `<<<` is just 3 trains, not one long train.
|
algorithms
|
def is_valid_train_arrangement(before, after):
if len(before) != len(after):
return False
l, r = 0, 0
for b, a in zip(before, after):
if b == '>':
if l != 0:
return False
r += 1
if a == '<':
if r != 0:
return False
l -= 1
if b == '<':
if r != 0 or l == 0:
return False
l += 1
if a == '>':
if l != 0 or r == 0:
return False
r -= 1
return l == 0 and r == 0
|
The Train Problem
|
645e541f3e6c2c0038a01216
|
[
"Algorithms",
"Strings",
"Performance"
] |
https://www.codewars.com/kata/645e541f3e6c2c0038a01216
|
6 kyu
|
# Background
Palindromes are a special type of number (in this case a non-negative integer) that reads the same backwards as forwards. A number defined this way is called __palindromic__.
* The following numbers are palindromes: `0`, `252`, `769967`, `1111111`.
* The following numbers are __not__ palindromes: `123`, `689`, `565656`, `12345432`.
# Problem Description
In this kata, you are required to build a function that receives two arguments, `a` and `b`, and returns the number of integer palindromes between `a` and `b` inclusive.
# Examples
* If `a` is `6` and `b` is `11`, the function should output `5` because there are 5 palindromes between 6 and 11 inclusive: `6`, `7`, `8`, `9` and `11`.
* If `a` is `150` and `b` is `250`, the function should output `10` because there are 10 palindromes between 150 and 250 inclusive: `151`, `161`, `171`, `181`, `191`, `202`, `212`, `222`, `232` and `242`.
* If `a` is `1002` and `b` is `1110`, the function should output `0`: there are no palindromes between 1002 and 1110 inclusive.
# Input Constraints
* Fixed test cases: `0` ≤ `a, b` ≤ `100` (one hundred)
* Small test cases: `0` ≤ `a, b` ≤ `10^5` (one hundred thousand)
* Medium test cases: `0` ≤ `a, b` ≤ `10^10` (ten billion)
* Large test cases: `0` ≤ `a, b` ≤ `10^15` (one quadrillion)
Ideally, a program should pass all the test cases in no more than 800 milliseconds.
# Edge Cases
* Note that `0` is palindromic.
* Numbers except `0` that start with `0` do __not__ count.
* If `a` and `b` are not integers, round `a` up and `b` down.
This is my first kata created. Hope you enjoy! <3
|
algorithms
|
from math import floor, ceil
def less_than(s):
if s[0] == '-':
return 0
n = int(s[0:(len(s) + 1) / / 2]) + 10 * * (len(s) / / 2)
if s[- (len(s) / / 2):] < s[len(s) / / 2 - 1:: - 1]:
return n - 1
return n
def count_palindromes(a, b):
a, b = ceil(a), floor(b)
if a > b:
return 0
return less_than(str(b)) - less_than(str(a - 1))
|
Palindrome Counter
|
64607242d3560e0043c3de25
|
[
"Number Theory",
"Mathematics",
"Performance"
] |
https://www.codewars.com/kata/64607242d3560e0043c3de25
|
4 kyu
|
# Find all the dividers!
You are given a list of prime numbers (e.g. ``[5, 7, 11]``) and a list of their associated powers (e.g. ``[2, 1, 1]``). The product of those primes at their specified power forms a number ``x`` (in our case ``x = 5^2 * 7^1 * 11^1 = 1925``).
### Your goal is to find all of the dividers for this number!
To do so, you have to multiply each prime number, from its power 0 to its power ``p`` in the power list, to every other prime, from their power 0 to their associated power ``p``.
Each result of those products is a divider of ``x``!
In our example: ``[1, 5, 7, 11, 25, 35, 55, 77, 175, 275, 385, 1925]``
Once you find those dividers, sort them in ascending order, and VOILA!
|
algorithms
|
from itertools import product
from operator import pow
from math import prod
def get_dividers(values, powers):
return sorted(prod(map(pow, values, x)) for x in product(* (range(p + 1) for p in powers)))
|
Dividers of primes
|
64600b4bbc880643faa343d1
|
[
"Mathematics"
] |
https://www.codewars.com/kata/64600b4bbc880643faa343d1
|
6 kyu
|
### Background
Suppose your doctor tells you that you have tested positive for a disease using a test that is 95% accurate. What's the probability that you actually have the disease? Surprisingly, the answer is much lower than 95%! Most doctors, not having much training in statistics, don't know this. The mathematical explanation of this is Bayes' Rule (see https://www.freecodecamp.org/news/bayes-rule-explained/). But an easier way of understanding it, especially for programmers, is to simulate the testing process.
### Task
Write a function *simulate* that takes 3 parameters:
(1) disease-rate - the percentage of people who have a particular disease;
(2) false-positive rate - the likelihood that somebody without the disease tests positive;
(3) a positive integer *n*.
The function should randomly assign, in proportion to the disease-rate, *n* people (numbered 1 to *n*) into two groups, sick (having the disease) and healthy. It should then simulate testing everyone for the disease. Assume that every sick person tests positive. *It should return the list of sick people and the number of positive tests.* The two return values should change every time it runs, even if the parameters remain the same.
NOTE: Your function's outputs will be subjected to various statistical tests. By random chance <b>a correct function will occasionally fail a test</b>. So it's worth trying the tests a few times if your first attempt fails.
**This is all you need to know to complete this kata.** The rest of the description explains how your function's results can be assessed to see if it's correctly simulating the likelihood that a person who tests positive actually has the disease. It's not essential to read it - but it is interesting :-).
### Explanation
The results of any test can be shown as follows:
<table style="width:50%">
<tr>
<td>Test Result</td>
<td>Sick</td>
<td>Healthy</td>
</tr>
<tr>
<td>Positive</td>
<td>True Positive</td>
<td>False Positive</td>
</tr>
<tr>
<td>Negative</td>
<td>False Negative</td>
<td>True Negative</td>
</tr>
</table>
Assuming that every sick person tests positive means that there are no false negatives - everyone who has the disease tests positive. Let TP be the number of sick people (who are true positives), and NP the number of positive tests. If you test positive, the likelihood that you have the disease is <sup>TP</sup>/<sub>NP</sub> .
### Example
Suppose that the testing process runs *simulate(1/100, 1/20, 1000)* twice. Setting the false-positive rate at *1/20* = 5% means that the test is 95% accurate, which is the scenario described above.
Suppose that run 1 returns [126, 265, 312, 353, 427, 445, 456], 51.
Suppose that run 2 returns [85, 89, 151, 181, 313, 465, 523, 531, 581, 629, 774, 847, 887, 889, 997], 75.
We know that:
(a) The number of sick people should be approximately the disease-rate multiplied by *n*. In this example this is (1/100) * 1000, which is 10.
(b) The number of positive tests should be approximately (the disease-rate + the false-positive rate) * *n* . In this example this is (1/100 + 1/20) * 1000, which is 60.
Since there are no false negatives, **the number of sick people divided by the number of positive tests** is the simulation's estimate of <sup>TP</sup>/<sub>NP</sub> , which is the likelihood that a positive test means that you are actually sick. The results are:
<table style="width:70%">
<tr>
<td></td>
<td>Number of Sick People<br> (Expected: 10)</td>
<td>Number of Positive Tests<br> (Expected: 60)</td>
<td>Estimate of Positive <br> Test -> Sick</td>
</tr>
<tr>
<td>Run 1</td>
<td align='center'>7</td>
<td align='center'>51</td>
<td>7/51 = 13.7%</td>
</tr>
<tr>
<td>Run 2</td>
<td align='center'>15</td>
<td align='center'>75</td>
<td>15/75 = 20%</td>
</tr>
</table>
The true likelihood (which can be calculated using Bayes' Rule) is 16.8%. The simulation result should get closer and closer to this value as *n* increases. Run 1 underestimated this value and Run 2 overestimated it. Using multiple runs makes it possible to assess whether your function is doing correct simulations. However, by statistical chance, a correct function might occasionally generate unlikely results, or time-out. So it's worth trying the codewars tests a few times if your first attempt fails.
In the scenario above, the likelihood that you have the disease is much lower than 95%! A positive test is definitely bad news (it raises the probability that you have the disease from 1% to almost 17%), but it's not nearly as bad as the accuracy of the test makes it seem. And it gets lower the rarer the disease is. This conclusion remains true if the test also has false negatives. That just makes the simulation slightly harder to program.
### Point of Interest
Bayes' Rule can also be used to solve the [Monty Hall Problem](https://www.codewars.com/kata/54f9cba3c417224c63000872).
|
reference
|
import random
import numpy
def simulate(disease_rate, false_positive_rate, n):
ntp = numpy . random . binomial(n, disease_rate)
nfp = numpy . random . binomial(n - ntp, false_positive_rate)
return [* random . sample(range(n), ntp)], ntp + nfp
|
Why You Shouldn't Believe Your Doctor
|
640f312ababb19a6c5d64927
|
[
"Simulation",
"Statistics",
"Tutorials"
] |
https://www.codewars.com/kata/640f312ababb19a6c5d64927
|
6 kyu
|
# Warcraft Series I - Mining Gold
Greetings!
The kata is inspired by my favorite strategy game, Warcraft 3, where players control units to gather resources and build their base. In this kata, the goal is to create a program that simulates the process of gathering gold from a mine and transporting it to a base.
The Workers are assigned to the gold mine and will automatically begin to gather gold from the mine. Once a Worker has collected a certain amount of gold, it will return to the base to deposit the gold at the Town Hall building.
## Input
* The parameter <code>path</code> represents the initial state of the mining field. It has a mine at index 0, represented by the letter <code>"M"</code>, and a base at index 4, represented by the letter <code>"B"</code>. The worker is initially positioned at index 2, which is a location between the mine and the base.<br>
* The parameter <code>time</code> is the number of iterations or ticks that the simulation should run. The method takes the input string, which represents the initial state of the simulation, and simulates the movement of workers for <code>times</code> iterations. The resulting state of the simulation is then converted into a list of strings, where each string represents a row of the grid.
<pre>
MiningRepresentation.generate("M..<B", 9);
</pre>
## Output
The output is a list or an array of strings representing the state of the map after each tick of time until time is over.
<pre>
M..<B // Worker goes to the mine
M.<.B
M<..B
*...B // Worker is mining gold
M>..B
M.>.B
M..>B
M...* // Worker brought the gold
M..<B
</pre>
## Explanation:
* <code>M</code> - Mine (location to gather gold)
* <code>B</code> - Base (location to bring gold)
* <code><</code> or <code>></code> direction where workers go (left/right)
* <code>*</code> - marks that Mine or Base is already busy by other worker
* <code>#</code> - marks collision (two workers at the same tile)
<br> Note: Mine and Base cannot contain more than one worker at a time
* <code>.</code> - Empty tile used to represent road between mine and base
### Example colisions
* Smooth Colision
<pre>
"M>....<B"
"M.>..<.B"
"M..><..B" // smooth collision
"M..<>..B"
"M.<..>.B"
</pre>
* Colision on same tile
<pre>
"M>...<B"
"M.>.<.B"
"M..#..B" // two workers on same tile
"M.<.>.B"
"M<...>B"
</pre>
## Tips:
* Mine will be always at index <code>0</code>, and Base at <code>last</code> index.
* Workers always spends one <code>tick/time</code> at base, in mine, or traveling one cell.
* There will be no test where workers spawn in collision, base or mine.
Currently there is no chance to get a random input that will have <code>#</code> or <code>*</code> in it. But the principle is very simple.
* Character <code>#</code> means that two workers are on same tile, and one goes to right and other to left(opposite dirrection).
* Character <code>*</code> means that the worker already arrived at one of the destionation so he will go to other one(mine to base or vice versa).
I'm still thinking if I should add more complex random tests that place workers anywhere at the start. Let me know your oppinion in discussions.
For better understanding check Example Tests for each case with comments inside. Good luck and be ready to work!
|
reference
|
class Worker ():
def __init__(self, position, direction, base):
self . position = position
self . direction = direction
self . base = base
def move(self):
if self . position == 0:
self . direction = 1
if self . position == self . base:
self . direction = - 1
self . position += self . direction
return self . position
class Coordinator:
def __init__(self, path):
self . workers = []
self . path_template = ["M"] + ["."] * (len(path) - 2) + ["B"]
self . parse(path)
def parse(self, path):
for i in range(len(path)):
if path[i] == "<":
self . workers . append(Worker(i, - 1, len(path) - 1))
elif path[i] == ">":
self . workers . append(Worker(i, 1, len(path) - 1))
def move(self):
for worker in self . workers:
worker . move()
def get_path(self):
path = self . path_template . copy()
for worker in self . workers:
match path[worker . position]:
case ".":
path[worker . position] = "<" if worker . direction < 0 else '>'
case "M":
path[worker . position] = "*"
case "B":
path[worker . position] = "*"
case "<":
path[worker . position] = "#"
case ">":
path[worker . position] = "#"
return "" . join(path)
def simulate_mining(path, time):
result = []
map = Coordinator(path)
for i in range(time):
result . append(map . get_path())
map . move()
return result
|
Warcraft Series I - Mining Gold
|
64553d6b1a720c030d9e5285
|
[
"Games",
"Object-oriented Programming"
] |
https://www.codewars.com/kata/64553d6b1a720c030d9e5285
|
6 kyu
|
# Intro:
In this kata you will create a linear feedback shift register (LFSR). An LFSR is used to generate a stream of (pseudo) random numbers/bits. It is most commonly implemented directly in hardware but here we'll do a software implementation.
# How does it work:
The register has XOR gates at given bit-positions (*pos*). These calculate a new bit by calculating XOR of the chosen bits. The register is shifted one to the right and the new bit is shifted in at the leftmost position of the register.
Here is a visualisation of an LFSR with a *size* of 5 bits and XOR connected to position 1 (D) and 3 (B).
```
+-<-(XOR)
| | |
+-> ABCDE
pos: 43210
```
Here would be the resulting states of the register, starting with *seed* `00010`:
```
ABCDE
00010
10001
01000
10100
01010
00101
00010
```
After which it would loop.
# Task:
Implement the function `lfsr(size, pos, seed)` so that it returns an iterable object holding the different states (integers) of the register over time.
- `size` is the size of the register in bits
- `pos` is an array of the XOR gate input positions
- `seed` is an integer describing the initial state of the register
# Note
- Indicies of the positions are from **right to left** (this way they stay at the same bit even when the size changes)
- There can be more than two inputs to the XOR. The XOR operation is associative.
- A register will be connected to a minimum of two positions.
# Next
If you liked to implement a LFSR you may like to try and reverse-engineer it in this [kata](https://www.codewars.com/kata/645cfe4ed2ce1b002a0429e7).
|
algorithms
|
def lfsr(size, pos, seed):
mask = sum(1 << i for i in pos)
while True:
yield seed
seed = seed >> 1 | ((seed & mask). bit_count() & 1) << size - 1
|
Linear Feedback Shift Register
|
645797bd67ad1d92efea25a1
|
[
"Algorithms",
"Binary",
"Bits"
] |
https://www.codewars.com/kata/645797bd67ad1d92efea25a1
|
6 kyu
|
The Fibonacci numbers are the numbers in the integer sequence:
`0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, ...`
Defined by the recurrence relation
Fib(0) = 0
Fib(1) = 1
Fib(2) = 1
Fib(i) = Fib(i-1) + Fib(i-2)
For any integer n, the sequence of Fibonacci numbers Fib(i) taken modulo n is periodic.
The Pisano period, denoted Pisano(n), is the length of the period of this sequence.
For example, the sequence of Fibonacci numbers modulo 3 begins:
0, 1, 1, 2, 0, 2, 2, 1, 0, 1, 1, 2, 0, 2, 2, 1, 0, 1, 1, 2, 0, 2, 2, 1, ...
This sequence has period 8. The repeating patter is `0, 1, 1, 2, 0, 2, 2, 1`
So `Pisano(3) = 8`
Your task is to write the Pisano function that takes an integer `n` and outputs the length of pisano period.
Once you've been able to solve this kata, a <a href="https://www.codewars.com/kata/65de16794ccda6356de32bfa">performance version</a> of this problem is awaiting you.
|
algorithms
|
def pisano(n):
a, b, k = 1, 1, 1
while (a, b) != (0, 1):
a, b = b, (a + b) % n
k += 1
return k
|
Pisano Period
|
5f1360c4bc96870019803ae2
|
[
"Mathematics",
"Algorithms",
"Arrays"
] |
https://www.codewars.com/kata/5f1360c4bc96870019803ae2
|
7 kyu
|
## <span style="color:#0ae">Introduction</span>
A [look-and-say sequence](https://en.wikipedia.org/wiki/Look-and-say_sequence) is an integer sequence. To generate a member of the sequence from the previous member, read off the digits of the previous member, counting the number of digits in groups of the same digit.
Examples:
`1` ⇒ "one `1`" ⇒ `11`
`21` ⇒ "one `2`, one `1`" ⇒ `1211`
Starting with `1`, the sequence begins with `1`, `11`, `21`, `1211`, `111221`, `312211`, `13112221`, ...
Starting with `7`, the sequence begins with `7`, `17`, `1117`, `3117`, `132117`, `1113122117`, ...
## <span style="color:#0ae">Task</span>
Given a number `$n$`, member of a look and say sequence, compute the starting number of the sequence, i.e. a number `$s$` such that:
- the input number `$n$` can be generated from `$s$` using 0 or more look and say steps
- `$s$` can't be generated from a different number using look and say algorithm
**Note:** In this kata all numbers (including starting numbers) contain at most 9 consecutive identical digits.
#### Input
- `n` *[integer]*
A member of a look and say sequence. Range: `$0$`–`$10^{180}$`
#### Output *[integer]*
The starting number of the sequence.
## <span style="color:#0ae">Examples</span>
- **`starting_number(2)` ⇒ `2`**
`2` can't be generated using look and say algorithm
- **`starting_number(23)` ⇒ `333`**
`23` is generated from `33`
`33` is generated from `333`
`333` can't be generated
|
reference
|
def starting_number(n):
a, b = str(n), ''
while a != b and len(a) % 2 == 0 and '0' not in a[:: 2] and all(x != y for x, y in zip(a[1:: 2], a[3:: 2])):
a, b = '' . join(a[k + 1] * int(a[k]) for k in range(0, len(a), 2)), a
if a[0] == '0' and len(a) > 1:
return int(b)
if '00' in a or (len(a) == 2 and a[- 1] == '0' and a[0] != '1'):
return int(a)
return int(a)
|
Reverse look and say
|
644ff2d6080a4001ff59a3b9
|
[
"Fundamentals",
"Mathematics"
] |
https://www.codewars.com/kata/644ff2d6080a4001ff59a3b9
|
6 kyu
|
"Pits" and "lands" are physical features on the surface of a CD that represent binary data. Pits are small depressions or grooves on the surface of the CD, while lands are flat areas between two adjacent pits.
The pits and lands themselves do not directly represent the zeros and ones of binary data. Instead, Non-return-to-zero, inverted encoding is used: a change from pit to land or land to pit indicates a one, while no change indicates a zero.
In this Kata, you should implement a function, that takes integer in range [0..255] (8 bits), and returns combination of pits and lands that encode the number.
Result should have format of string: `PLLPL...` where `P` represents pit and `L` represents land. Combination should always start with pit.
Numbers should be encoded in little-endian, which means you start from least significant bit.
### Example
Input: `5`
Binary representation (8 bits): `00000101`
Output: `PLLPPPPPP`
Explanation:
1. Starts from P as per description
1. Changes to L because first bit is `1`
1. Stays L because second bit is `0`
1. Changes to P because third bit is `1`
1. Stays P because fourth bit is `0`
1. Stays P till the end because all subsequent bits are `0`
|
reference
|
def encode_cd(n):
if n > 255:
return - 1
forma = format(n, '08b')
form = forma[:: - 1]
res = "P"
p = 'P'
l = 'L'
for f in form:
if f == '1': # 1 it is always change letter to another letter
p, l = l, p
res += p
return res
|
Encode data on CD (Compact Disc) surface
|
643a47fadad36407bf3e97ea
|
[
"Binary"
] |
https://www.codewars.com/kata/643a47fadad36407bf3e97ea
|
7 kyu
|
Many programming languages provide the functionality of converting a string to uppercase or lowercase. For example, `upcase`/`downcase` in Ruby, `upper`/`lower` in Python, and `toUpperCase`/`toLowerCase` in Java/JavaScript, `uppercase`/`lowercase` in Kotlin.
Typically, these methods won't change the size of the string.
For example, in Ruby, `str.upcase.downcase.size == str.size` is `true` for most cases.
However, in some special cases, the length of the transformed string may be longer than the original. Can you find a string that satisfies this criteria?
For example, in Ruby, That means `str.upcase.downcase.size > str.size`
You should just set the value of `STRANGE_STRING` to meet the previous criteria.
Note: Meta programming is not allowed in this kata. So, the size of your solution is limited.
|
reference
|
STRANGE_STRING = 'ß'
|
Up and down, the string grows
|
644b17b56ed5527b09057987
|
[
"Strings",
"Puzzles"
] |
https://www.codewars.com/kata/644b17b56ed5527b09057987
|
8 kyu
|
```if:csharp
Given 8 byte variable (Uint64) extract `length` of bits starting from least significant bit* and skipping `offset` of bits.
```
```if:python
Given `int` variable extract `length` of bits starting from least significant bit* and skipping `offset` of bits.
For convenience sake only first 64 bits of input variable will be used for encoding value. `offset` and `length` may be arbitrarily large.
```
```if:javascript
Given `BigInt` variable extract `length` of bits starting from least significant bit* and skipping `offset` of bits.
For convenience sake only first 64 bits of input variable will be used for encoding value. `offset` and `length` may be arbitrarily large.
```
All input values will be non-negative.
Examples
|input|offset|length|result|
| -| -| -| -|
|0xAF|4|0|0x0|
|0xAF|0|4|0xF|
|0xAF|4|4|0xA|
|0xAB00EF|4|16|0xB00E|
|0xAA00BB00CC| 0xF0000000| 0x64| 0x0|
\*LSb - Least Significant bit - bit denoting smallest value in the number i.e. 0 or 1.
|
reference
|
def extract_bits(o, _, O): return o >> _ & ~ - (1 << O)
|
Extract bits from integer
|
6446c0fe4e259c006511b75e
|
[
"Bits"
] |
https://www.codewars.com/kata/6446c0fe4e259c006511b75e
|
7 kyu
|
Confusion, perplexity, a mild headache. These are just a sample of the things you have experienced in the last few minutes while trying to figure out what is going on in your code.
The task is very simple: accept a list of values, and another value `n`, then return a new list with every value multiplied by `n`. For example, `[1, 2, 3]` and `4` should result in `[4, 8, 12]`.
While writing the function, you even added some debugging lines to make sure that you didn't mess anything up, and everything looked good! But for some reason when you run the function it always seems to return an empty list, even though you can clearly see, that the list *should* have the right values in it! Somehow, the values are simply disappearing! Is this a bug in the programming language itself...?
|
bug_fixes
|
def mul_by_n(lst, n):
print("Inputs: ", lst, n) # Check our inputs
result = [x * n for x in lst]
print("Result: ", result) # Check our result
return result
|
Vexing Vanishing Values
|
644661194e259c035311ada7
|
[
"Debugging",
"Refactoring"
] |
https://www.codewars.com/kata/644661194e259c035311ada7
|
8 kyu
|
# Rook Count Attack
This kata is focused on counting the number of attacks between rooks that are attacking each other on a standard 8x8 chessboard. A <code>rook</code> is a chess piece that can move horizontally or vertically across any number of squares on the board.
### How the rook moves
<img src="https://live.staticflickr.com/65535/52831722112_d15d939f16_z.jpg" style="height:300px; width:300px;" alt="Rook Moves">
### Input
The input for this kata is a bidimensional array that represents the positions of the rooks on the board.
* Each element in the array is a two-element array that represents the x and y coordinates of a rook on the board(check test section).
* The order of rooks in the array is random and there will not be any duplicate rooks in the same tile.
* Also the rooks are not removed from board an attack happened.
Rooks on [c6, f4, f6] will be <code>[2,5], [5,3], [5,5]</code>
### Output
The output for this kata is an integer that represents the number of attacks between rooks that are attacking each other. A rook is considered to be attacked by another rook if they are on the same row or column.
### Example 1
The image bellow contains 3 rooks, <code>[c6, f4, f6]</code>. All three of them are attacking each other. Your solution should return <code>2</code> as number of attacks between all rooks. The counter attacks are not counted for this kata.
<img src="https://live.staticflickr.com/65535/52832773923_896fb43c4d.jpg" width="300" height="300" alt="Three Rooks">
### Example 2
The example below shows how to count the number of attacks correctly. Firstly, is counted the attack that does the <code>b4</code> rook on <code>b6</code> rook. The rook on <code>b6</code> attacks just the rook on <code>d6</code>, because in this kata, counter-attacks(when 2 rooks are on same line and can attack each other) are counted just as <code>ONE</code> attack. So the rook on <code>b6</code> can't attack the rook that had already attacked it, and attacks just the one on <code>d6</code>
In other words, there is a chain of attacks between all rooks, and you need to find how many attacks are there between all rooks on the chess board. The result for the example below is <code>5</code>, as shown in the image. Please note that rooks are not removed from the board after their attacks were counted.
<img src="https://live.staticflickr.com/65535/52837856510_ec4ec63582_z.jpg" width="300" height="300" alt="Rook Attacks"/>
> Every rook can attack just once. If two rooks are on the same line, then just <code>one</code> attack is counted(1 -> 2). If three rooks are on the same line, then there are <code>two</code> attacks between them(1 -> 2 -> 3).
Check Tests in case something is not clear. <br>
Good luck and have fun.<br>
PS: There are 500_000 random tests with up to 64 rooks on same board(8x8).
<hr>
This is my first kata :) <br>
Fell free to contribute and to improve this kata
|
reference
|
def count_attacking_rooks(rooks):
s1 = set(item[0] for item in rooks)
s2 = set(item[1] for item in rooks)
return len(rooks) * 2 - len(s1) - len(s2)
|
Rook Count Attack
|
64416600772f2775f1de03f9
|
[
"Arrays"
] |
https://www.codewars.com/kata/64416600772f2775f1de03f9
|
6 kyu
|
You have done some data collection today and you want the data to be well presented by a graph so you have decided to make a quick diagram. Suppose that for this kata your data is presented by an array by their value eg [10,5,3,1,4], then you must present your data as follows:
```
for data = [10,5,3,1,4] :
____ ........................ ^ 10
| |........................ | 9
| |........................ | 8
| |........................ | 7
| |........................ | 6
| | ____ .................. | 5
| || |............ ____ | 4
| || | ____ ......| | | 3
| || || |......| | | 2
| || || | ____ | | | 1
| || || || || | | 0
```
#### GOOD TO KNOW :
* Each bar is always of width 6.
* The vertical axis must be surrounded with one space character on each side.
* No trailing spaces on any line.
* For this kata we use :
- the following characters : ```'_',' ','|','.','^'```.
- some numbers.
* Return type :
- Your code must return a character string joined by ```\n```.
- ```[]``` and ```[0]``` has different returns ```""``` and ```" ____ ^ 0"```
#### CRITERIA :
- The length of the array is always less than ```50```.
- The value of a data is also less than ```50 and always positive```.
GOOD LUCK :)
|
games
|
def graph(arr):
graph = []
top = max(arr, default=- 1)
for y in range(top, - 1, - 1):
row = []
for value in arr:
if value == y:
row . append(' ____ ')
elif value < y:
row . append('......')
else:
row . append('| |')
row . append(f' { "^|" [ y < top ]} { y } ')
graph . append('' . join(row))
return '\n' . join(graph)
|
Let's do a fun graph
|
6444f6b558ed4813e8b70d43
|
[
"Strings",
"Arrays",
"ASCII Art"
] |
https://www.codewars.com/kata/6444f6b558ed4813e8b70d43
|
6 kyu
|
# Task
Your task is to check whether a segment is completely in one quadrant or it crosses more.
Return `true` if the segment lies in two or more quadrants.
If the segment lies within only one quadrant, return `false`.
There are two parameters: `A` _(coord)_ and `B` _(coord)_, the endpoints defining the segment `AB`.
**No coordinate will be zero; expect that all X and Y are positive or negative.**
# Examples
1. This whole segment is in the first quadrant.
```
[(1, 2), (3, 4)] -> false
```

2. This segment intersects the Y axis, therefore being in two quadrants: I and II.
```
[(9, 3), (-1, 6)] -> true
```

3. This segment is completely in the second quadrant.
```
[(-1, 6), (-9, 1)] -> false
```

# Predefined
There is a class named `coord`/`Coord` (see in code). It has the following members:
* _`(constructor)`_: Constructs the coordinate
- `x` _(number)_: The X coordinate
- `y` _(number)_: The Y coordinate
* `x` _(number)_: The X coordinate
* `y` _(number)_: The Y coordinate
~~~if:cpp,c
* `operator==` _(bool)_: Compares two coordinates if they're the same
* `str` _(string)_: Turns coordinate into string
~~~
~~~if:javascript,typescript
* `equal` _(bool)_: Compares two coordinates if they're the same
- `c` _(coord)_: The coordinate to compare with
* `toString` _(string)_: Turns coordinate into string
~~~
# Task Series
1. [Quadrants](https://www.codewars.com/kata/643af0fa9fa6c406b47c5399)
2. Quadrants 2: Segments _(this kata)_
|
reference
|
def quadrant_segment(A, B):
A = A[0] < 0, A[1] < 0
B = B[0] < 0, B[1] < 0
return A != B
|
Quadrants 2: Segments
|
643ea1adef815316e5389d17
|
[
"Fundamentals",
"Mathematics",
"Geometry"
] |
https://www.codewars.com/kata/643ea1adef815316e5389d17
|
7 kyu
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.