Interpreting the Weight Space of Customized Diffusion Models

Amil Dravid*1,2, Yossi Gandelsman*1, Kuan-Chieh (Jackson) Wang2, Rameen Abdal3, Gordon Wetzstein3, Alexei A. Efros1, Kfir Aberman2
1UC Berkeley, 2Snap Inc., 3Stanford University

*Equal contribution

arXiv Video Code+Data (end of June release)

We discover a subspace in diffusion weights that behaves as an interpretable latent space over customized models.

Abstract

We investigate the space of weights spanned by a large collection of customized diffusion models. We populate this space by creating a dataset of over 60,000 models, each of which is fine-tuned to insert a different person’s visual identity. Next, we model the underlying manifold of these weights as a subspace, which we term weights2weights. We demonstrate three immediate applications of this space -- sampling, editing, and inversion. First, as each point in the space corresponds to an identity, sampling a set of weights from it results in a model encoding a novel identity. Next, we find linear directions in this space corresponding to semantic edits of the identity (e.g., adding a beard). These edits persist in appearance across generated samples. Finally, we show that inverting a single image into this space reconstructs a realistic identity, even if the input image is out of distribution (e.g., a painting). Our results indicate that the weight space of fine-tuned diffusion models behaves as an interpretable latent space of identities.

Creating weights2weights Space

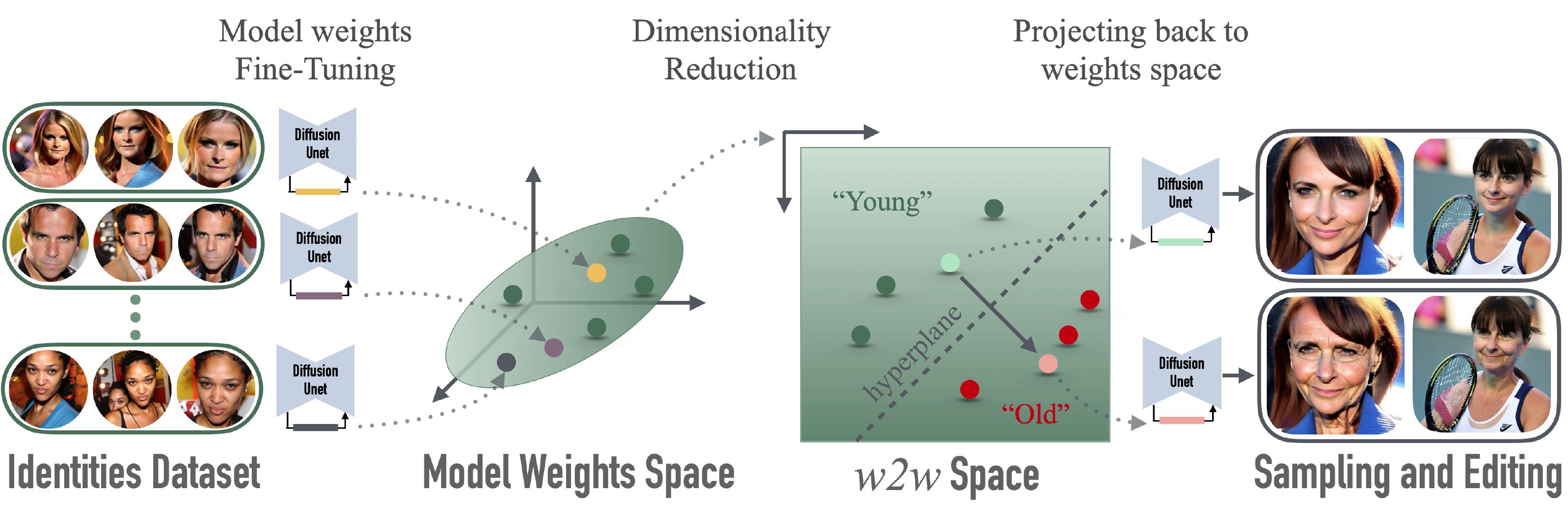
scheme


We create a dataset of model weights where each model is finetuned to encode a specific identity using low-rank updates (LoRA). These model weights lie on a weights manifold that we further project into a lower-dimensional subspace spanned by its principal components. We term the resulting space weighst2weights (w2w), in which operations transform one set of valid identity-encoding weights into another. We train linear classifiers to find separating hyperplanes in this space for semantic attributes. These define disentangled edit directions for an identity-encoding model in weight space.

Identity Editing

Given an identity parameterized by weights, we can manipulate attributes by traversing semantic directions in the w2w weight subspace. The edited weights result in a new model, where the subject has different attributes while still maintaining as much of the prior identity. These edits are not image-specific, and persist in appearance across different generation seeds and prompts. Additionally, as we operate on an identity weight manifold, minimal changes are made to other concepts, such as scene layout or other people. Try out the sliders below to demonstrate edits in w2w space.

Slide the bars to edit the identity.

Editing
0
0
0

Inversion

By constraining a diffusion model's weights to lie in w2w space while following the standard diffusion loss, we can invert the identity from a single image into the model without overfitting. Typical inversion into a generative latent space projects the input onto the data (e.g., image) manifold. Similarly, we project onto the manifold of identity-encoding model weights. Projection into w2w space generalizes to unrealistic or non-human identities, distilling a realistic subject from an out-of-distribution identity. We provide examples of inversion below with a variety of input types.

Click on an image to invert its subject into a model.

inversion rect1b rect2b rect3b

Sampling

Modeling the underlying manifold of identity-encoding weights allows sampling a new model that lies on it. This results in a new model that generates a novel identity that is consistent across generations. We provide examples of sampling models from w2w space below, demonstrating a variety of facial attributes, hairstyles, and contexts.

Click to sample an identity-encoding model.

sampling rect1 rect2 rect2 rect2 rect2

Connection to Generative Latent Spaces

w2w_vs_gan

As seen from the interactive examples above, weights2weights space enables applications analogous to those of a traditional generative latent space–-inversion, editing, and sampling–-but producing model weights rather than images. With generative models such as GANs, the instance is a latent mapping to an image, whereas the instance with weights2weights is a set of identity-encoding weights.

More Results


Composing Edits in Weight Space

compose


Continuous Control over Identity Edits

continuous


Identity Inversion + Editing

inversion_edit


Out-of-Distribution Identity Projection

ood_project


w2w Sampling and Nearest Neighbor Identities

sampling

Acknowledgments

The authors would like to thank Grace Luo, Lisa Dunlap, Konpat Preechakul, Sheng-Yu Wang, Stephanie Fu, Or Patashnik, Daniel Cohen-Or, and Sergey Tulyakov for helpful discussions. AD is supported by the US Department of Energy Computational Science Graduate Fellowship. Part of the work was completed by AD as an intern with Snap Inc. YG is funded by the Google Fellowship. Additional funding came from ONR MURI.

BibTeX

@misc{dravid2024interpreting,
      title={Interpreting the Weight Space of Customized Diffusion Models},
      author={Amil Dravid and Yossi Gandelsman and Kuan-Chieh Wang and Rameen Abdal and Gordon Wetzstein and Alexei A. Efros and Kfir Aberman},
      year={2024},
      eprint={2406.09413},
}